Tertiary and Secondary Structure Elasticity of Titin
Mechanical proteins confer structural support and mechanical compliance to biological cells and tissues, for example during muscular contraction. The protein titin provides the passive elasticity required to restore muscle to its resting length after contraction. Through its elasticity, titin protects muscle fibers also from mechanical injury.
Titin is the largest protein in nature, composed mainly of immunoglobulin-like (Ig- ) or fibronectin-III-like (FN-III) domains. The current understanding of titin's mechanical properties arose from single-molecule force spectroscopy investigations of isolated, native titin as well as recombinant fragments. From these experiments, a picture began to form describing how titin reacts to mechanical stretching forces. Upon stretching, titin's chain of domains first straightens without unfolding; this is followed by elongation of disordered segments; finally, at strong forces, the secondary structure of titin's Ig- and FN-III domains unravels, a process referred to as rupture. Thus, in addition to the entropic elasticity conferred by the protein's disordered domains, titin's mechanical elasticity can be further classified, into two distinct regimes: tertiary structure elasticity due to domain-domain straightening, and secondary structure elasticity due to the unraveling of domains.
Using the crystal structure of a six-Ig chain (Figure 1; von Castelmur et al., 2008), a series of computational and theoretical investigations were carried out to characterize both the tertiary and secondary structure elasticity of titin.
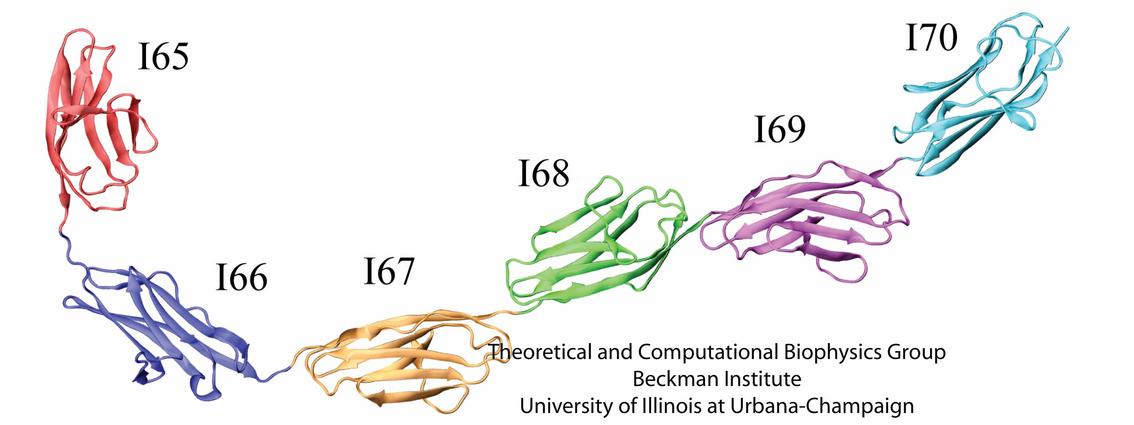 |
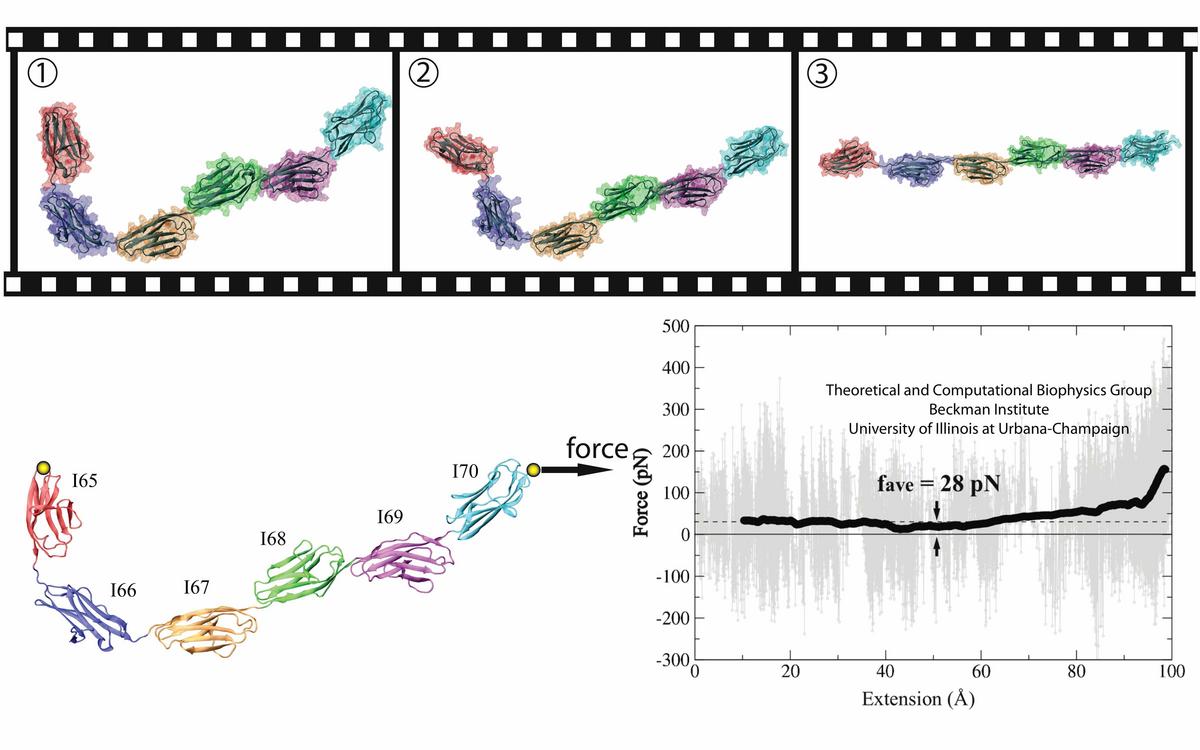
Figure 1 - The structure of six Ig-domains linked into a protein chain. Each domain is colored differently for identification. |
Tertiary Structure Elasticity of the six-Ig chain
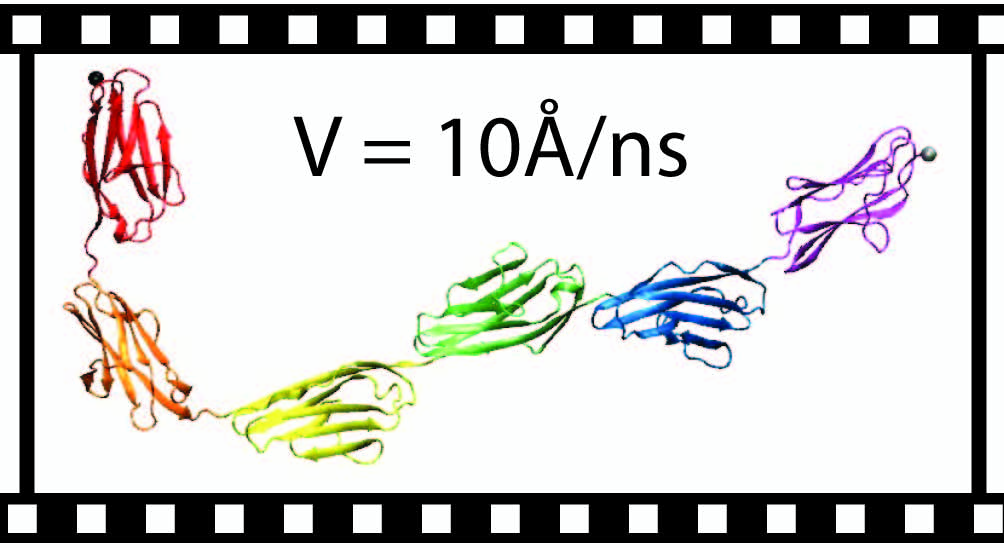
Using the Steered Molecular Dynamics methodology (SMD), the six-Ig chain shown in Figure 1 was extended with a small force (<200pN). The configuration of the six-Ig chain during the SMD simulation is displayed in Figure 2, and a movie for this trajectory is available here (8.2MB). This simulation enables probing of the soft tertiary structure elasticity of the six-Ig chain, as the chain can be extended without unraveling the individual domains. Forces applied on the chain can be measured, and the force-extension plot can be generated. As shown in Figure 2, the force required to extend the Ig chain is just few tens of pN. One can also notice that a sharp rise in force when extension reaches beyong 90 A.Theoretical Modeling of the Tertiary Structure Elasticity
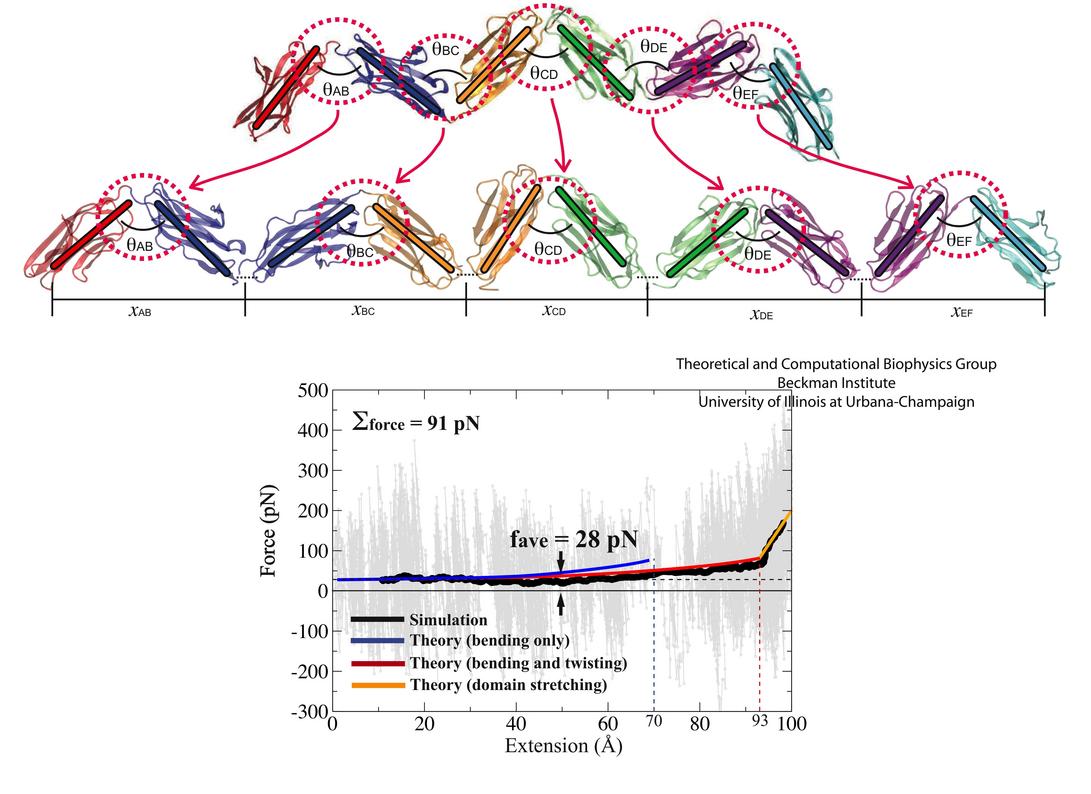
To understand the energetic requirements for extending the six-Ig chain, a series of free-energy calculations were carried out using the Adaptive Biasing Force method (ABF). The ABF methodology permits computation of the free enrgy of a structural transition along a pre-defined reaction coordinate. For the case of the six-Ig chain, the domains have several degree of freedoms, the predominant ones being the hinge-like bendings of domain pairs, and the twistings around the linkers. Free-energy calculations were performed to investigate the energetic costs of these motions.Having obtained the free energy of the domain pair motions, these energetics can then be used to reconstruct the force response of a full, six-Ig chain. The recipe of doing so is illustrated in Figure 3. Each domain pair is linked together schematically, and the energetics of the hinge bending motions can be combined as described in Lee et al., 2007 and Lee et al., 2010. The result of the calculation, shown in the plot in Figure 3, demonstrates the validity of this simple model. The force-extension curve generated in the SMD simulation can be described well by the theoretical modeling of the six-Ig chain after incoporating all the major degree of freedoms of the domains.
Secondary Structure Elasticity of the Six-Ig Chain
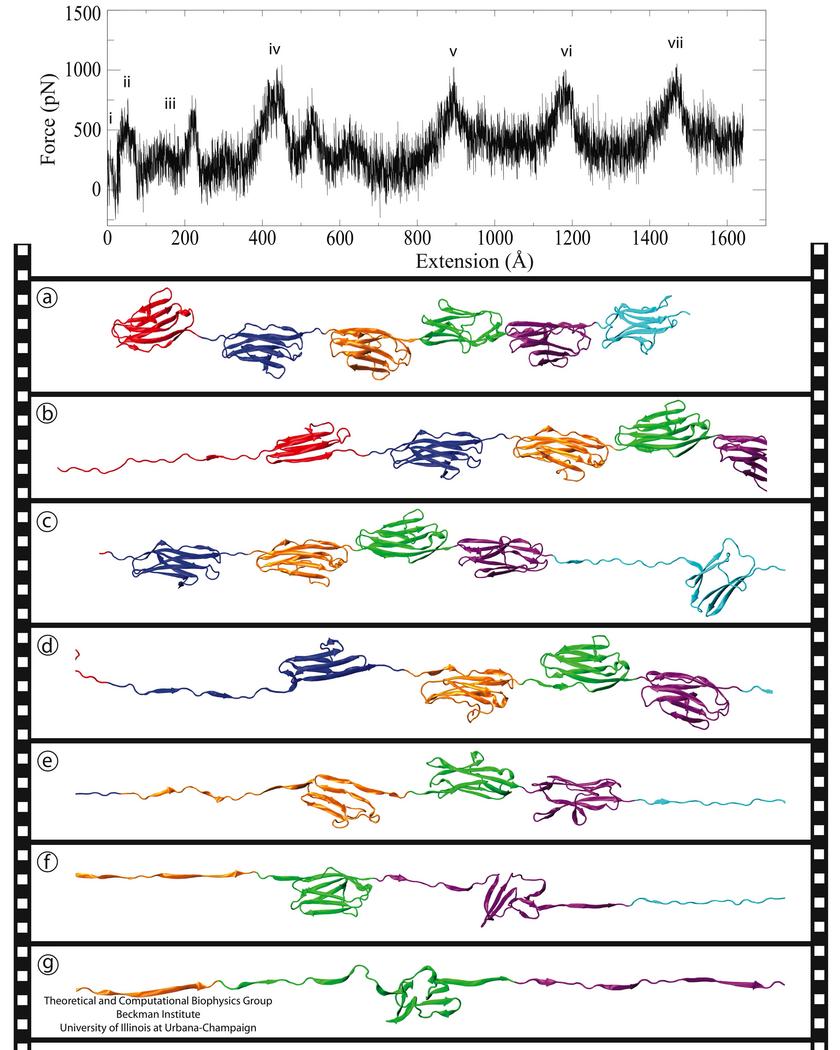
Force spectroscopy experiments unfolding polyprotein Ig-chains have produced a distinct sawtooth force-extension profile interpreted as the sequential rupture of individual Ig-domains. All-atom molecular dynamics simulations up to this point have been limited by computational resources and by the availability of relevant structures to simulating the unfolding of only single Ig-domains. Recent strides in computational efficiency permit us now to carry out SMD simulations to completely extend and unfold six-Ig titin chain.The SMD simulation of the full unfolding of the six-Ig chain is described in Figure 4, with the movie for this trajectory available here (18MB). The force-extension curve displays the sawtooth profile vividly, with each force peak corresponds to the unraveling of an Ig domain. It is seen that the order of domain unraveling is I65, I70, I66, I67, I69, and finally I68, with the terminal domains rupturing before the ones in the middle of the Ig chain. Unraveling of an Ig domain can also be seen to stabilize other domains.
Dragging Protein through Water
The non-zero force required to extend the titin segment during early extension as shown in Figure 3 is due to hydrodynamic drag force, as water molecules are included explicitly in the stretching simulation. The drag force is roughly linear with the velocity with which the titin segment is stretched, i.e., for the stretching velocity of 10 Å/ns, there is approximately 28 pN of drag force (dashed line in Figure 3). The stretching force due to purely tertiary structure elasticity of the titin segment cannot manifest until it rises above the 28 pN drag force, which occurs later during the stretching simulation after 60 Å extension.The hydrodynamic drag force can be reduced by simply slowing down the stretching velocity, but, for the same amount of extension, much more computer time is required. To better resolve the intrinsic tertiary structure elasticity of titin, another stretching simulation with a ten-fold reduced velocity was conducted, the two movies can be compared side-by-side below. The ten-fold slower stretching velocity means that the simulation is ten times more computationally costly, but the hydrodynamic drag force is reduced to 2.8 pN, i.e., near zero. As a result, the force-extension plot obtained in the second simulation reflects fully the tertiary structure-based force response of the titin segment, and is also well described by the statistical mechanical theory mentioned above.
Figure 5 - The trajectories from two steered molecular dynamics simulations extending the originally crescents-shaped titin segment containing six Ig domains. The second simulation employes a stretching velocity that is ten times slower than the first simulation. The protein segment can be seen to experience more diffusive motion for the case of slower stretching velocity. Click on the images to view movies.
Additional Movies
IG6_extend_only.mpg (10.6MB): an SMD simulation of pulling apart the IG6 chain with small forces, triggering the tertiary structure elasticity of the protein chain. Note all protein domains retain their secondary structure.
IG6_noDS_zoom.mpg (23MB): an SMD simulation of pulling apart the IG6 chain with larger forces, triggering the secondary structure elasticity of the protein chain. Note the protein domains unravel one by one.
Related publications
Tertiary and secondary structure elasticity of a six-Ig titin chain.
Eric H. Lee, Jen Hsin, Eleonore von Castelmur, Olga Mayans, and Klaus Schulten.
Biophysical Journal, 98:1085-1095 (2010).
Molecular origin of the hierarchical elasticity of titin: simulation, experiment and theory.
Jen Hsin, Johan Strumpfer, Eric H. Lee, and Klaus Schulten.
Annual Review of Biophysics, 40:187-203 (2011).
Improved resolution of tertiary structure elasticity in muscle protein.
Jen Hsin and Klaus Schulten.
Biophysical Journal, 100:L22-L24 (2011).
Investigators
Collaborator
Olga Mayans (University of Liverpool)
Related web pages on our site
Unfolding titin immunoglobulin domains
The chain-like elasticity of titin
Mechanical Strength of the Z1Z2-Telethonin Complex
Page created and maintained by Jen Hsin and Eric H. Lee.