Empirical Nanotube Model for Biological Applications

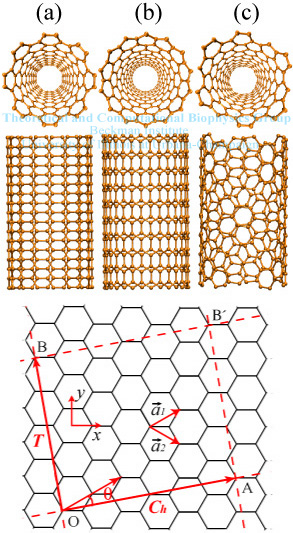Structure of Nanotubes Figure 1: Structure of nanotubes

Introduction to Carbon Nanotubes

A single-walled carbon nanotube (SWNT) can be imagined as a seamless cylinder formed by a hexagonal graphite layer (see Fig. 1). Only a few nm's in diameter, a SWNT can grow as long as several microns making it a perfect one-dimensional material. Recently, growth of mm to cm scale long SWNTs has also been reported. Depending on the synthesis procedures, SWNTs may nest inside each other to form "Russian dolls", known as multi-walled carbon nanotubes (MWNTs). After the discovery of carbon nanotubes (CNTs) in 1991, the world envisioned a rapid growth of nanotube research. Both theoretical and experimental investigations show that the unique structure gives nanotubes remarkable mechanical, electronic, and optical properties. The strong covalent bonds between carbon atoms of CNTs lead to a high Young's modulus close to 1.25 TPa, about five times the value of steel. In contrast to ordinary materials, different types of SWNTs can be either metallic or semiconducting. The high aspect ratio (length / diameter) qualifies CNTs as excellent field emission devices. Due to these amazing properties, CNTs have so many applications: field effect transistor, nanoelectromechanical systems, flat-panel display,chemical sensor, biosensor, molecular channel, hydrogen fuel cell, to name a few.

SWNTs can be classified according to how they are mapped into a single graphite layer. Considering the hexagonal lattice shown at the bottom of Fig. 1, the unit vectors of the lattice are defined by a1 and a2 with the C-C bond length being 1.42 Å. A SWNT is constructed by rolling the graphite layer along a certain direction Ch = n a1 + m a2 making OB and AB' coincide. Perpendicular to Ch, the vector T points to the long axis of the SWNT. Ch and T are referred as chiral vector and translational vector, respectively. Together they define the unit cell of a SWNT as the rectangle OAB'B. The chiral indices (n, m) are commonly used to label SWNTs. Alternatively, one can use $\theta$, the chiral angle between a1 and Ch to classify SWNTs. Due to the C6 symmetry of the hexagonal lattice, |$\theta$| ≤ 300. SWNTs with $\theta$ =300 or $\theta$=00 have the highest symmetry, known as armchair (Fig. 1a) or zigzag nanotubes (Fig. 1b). For the rest, they are generally referred as chiral nanotubes (Fig. 1c). It is well-known from tight-binding (TB) theory that a SWNT is metallic when (n - m) is a multiple of 3. Otherwise, it is semiconducting.

Polarizable Carbon Nanotube Model

In order to study biological applications of SWNT segments such as artificial molecular channels conducting water, protons, ions, or polymers, one needs to develop an accurate and efficient model for SWNTs that can be used in conjunction with molecular dynamics simulations. Instead of picking available parameters from existing CHARMM or AMBER force fields, three additional factors need to be considered, namely, edge-saturation, atomic partial charges, and polarizability to yield a more realistic description of SWNTs. Chemically shortened SWNTs are saturated by carboxylic acid groups at the open ends, which prevents geometry reconstruction at the tube edges caused by the dangling bonds, so edge-saturation seems to be an appropriate choice for finite-length SWNTs. There could be a significant amount of charge transfer between the saturation group and the edge carbon atoms, therefore the atomic partial charges of the whole molecule have to be carefully determined. It is also important to include the polarizability, or dielectric response of SWNTs in the model, because SWNTs are highly polarizable due to their delocalized $\pi$-electrons, which respond strongly to external fields. Theoretical investigations revealed that metallic nanotubes can effectively screen out the long range Coulomb potential along the axial direction, while screening effects in semiconducting tubes are weaker. Neglecting the polarization of SWNTs in molecular channel simulations could be problematic, because the filling and transport properties of small molecules are sensitive to their interactions with SWNTs.

In recent publications (1, 2), we developed a semi-empirical SWNT model suitable for studying biomolecular systems. In this model, SWNTs were saturated with hydrogen atoms and atomic partial charges (RESP charges) were parameterized for (6,6) SWNTs at various lengths. The dielectric response of a SWNT was calculated based on a self-consistent TB model, and good agreement is seen with that from density functional theory (DFT) calculations. The significance of the new SWNT model was illustrated by examining the interaction potential between a water molecule and a short (6,6) SWNT segment as well as the dynamics of a SWNT-K+ complex.

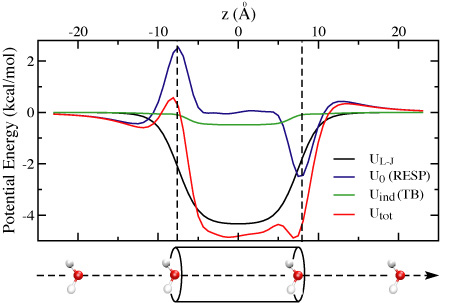  Figure 2: Interaction potential between a water molecule and a 15 Å long (6,6) SWNT.

SWNT Water Channel

In Fig. 2, we compare four interaction potential profiles:
(1) UL-J, van der Waals potential;
(2) U0, the static Coulomb interaction from bare atomic partial charges;
(3) Uind, the Coulomb potential from induced charges;
(4) Utot, the total interaction potential.
As one can see, UL-J is symmetric with a simple potential well of -4.34 kcal/mol in the middle of the tube, and U0 strongly affects the energetics of water entering the tube. At the left side, a water molecule encounters a shallow potential well of -0.44 kcal/mol followed by a high potential barrier of 2.97 kcal/mol. It experiences a small barrier and a deep well when entering the SWNT from the right side in the given, fixed orientation. In the middle of the tube, U0 is nearly vanishing. Uind has

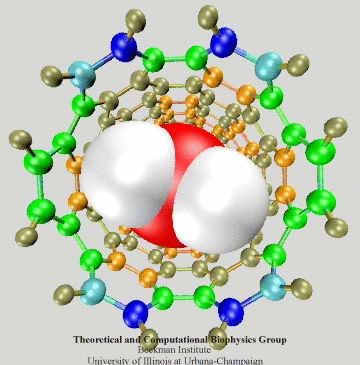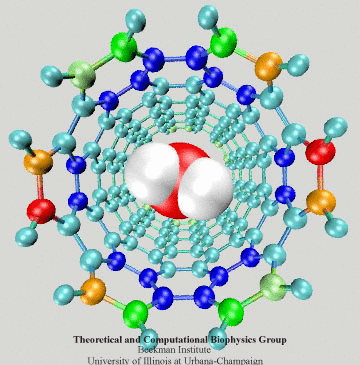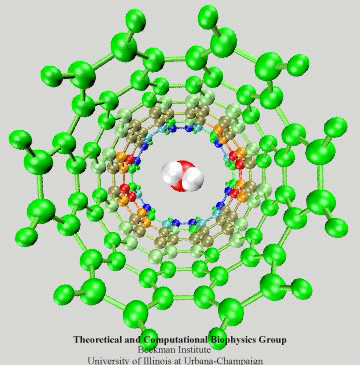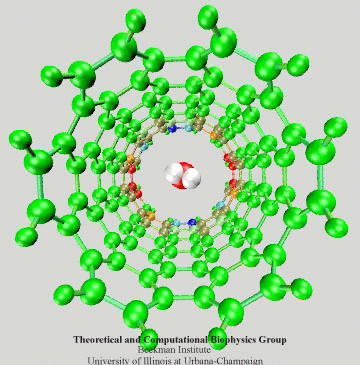  Figure 3: Electrons of the SWNT dragged by a passing water molecule.


a similar shape as UL-J, but is an order of magnitude smaller. By putting them together, the major contribution of Utot stems from UL-J, but at the edges, the shape is dominated by U0. The charge transfer between hydrogen and carbon atoms creates bumps in Utot, which may slow down the transport of water molecules through SWNTs. Compared to the bare UL-J, the potential well of Utot is lowered by 0.55 kcal/mol mainly due to Uind. Previous studies indicated that water flow is primarily limited by the barriers at the entry and exit of the nanotube, so it is critical to include both UL-J and U0 near the tube edges. Although Uind is small compared to other contributions in Fig. 2, it becomes significant for ions and charged molecules. For instance, the interaction energy between a point charge of +e at the tube center and its image charges on the same SWNT segment as considered here is found to be 15.2 kcal/mol. External electric fields are commonly used to increase or decrease ion flow. Neglecting the screening ability of SWNTs should exaggerate the impact of external fields.

To have an intuitive view of the polarization effect of the SWNT, we show in Fig. 3 how the induced charges of the SWNT change as a water molecule is passing through the nanotube. The SWNT is colored according to induced charges (blue: positive, red: negative).


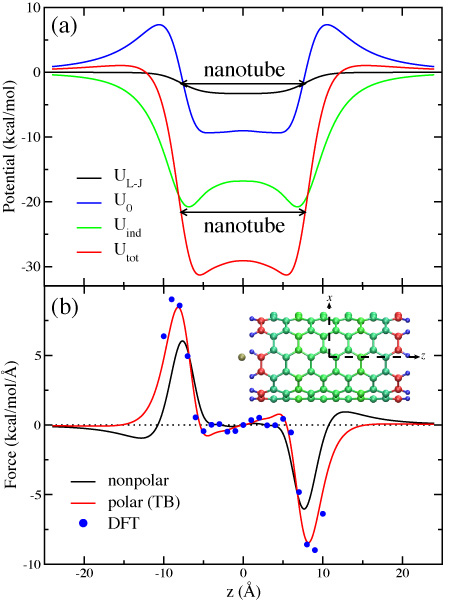  Figure 4: SWNT-K+ interaction potential and the force experienced by the ion.

Ion-Nanotube Terahertz Oscillator

A great example illustrating the polarization effect of SWNTs has been discovered recently by us (see reference). The example involves the motion of a potassium ion, K+, inside a SWNT segment as shown at the inset of Fig. 4. The dielectric response of the SWNT to the K+ was computed on-the-fly along with the motion of the ion. By positioning the ion along the nanotube long axis, we first examined the SWNT-K+ interaction potential. As shown in Fig. 4a, it is found that UL-J (defined above) is rather small and that the Coulomb potentials U0 and Uind are dominant. Although U0 exhibits a potential well inside the SWNT, a large access barrier of about 7.02 kcal/mol arising in UL-J + U0 seems to keep the potassium ion from entering the SWNT. When Uind is added, however, the access barrier drops to only 1.05 kcal/mol in Utot= UL-J + U0+Uind due to a considerable attraction between the K+ and the $\pi$-electrons of the SWNT. Also, the potential well inside the SWNT becomes even more attractive with a minimum of about -30 kcal/mol. This picture has been validated by comparing the forces acting on the K+ from the suggested model and from the density functional theory. A good agreement is found as shown in Fig. 4b. When the polarization effect is neglected, the force (black curve in Fig. 4b) becomes much weaker.

In order to couple the quantum mechanical description of SWNT polarizability to the classical motion of the potassium ion, the instantaneous atomic partial charges of the SWNT are updated constantly as the sum of initial partial charges, q0, and induced charges, δq. Attention needs to be paid to the form of the classical force on the K+. Let us write down Uind explicitly as

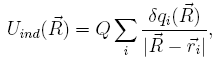
formula1

where Q and r, respectively, are the charge and coordinates of the K+, and the summation index, i, runs over all carbon atoms. In addition to the standard Coulomb force, an extra term appears proportional to the derivative of δq,

formula2
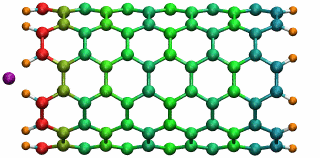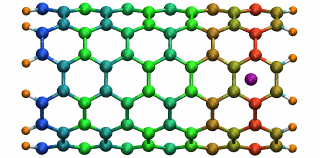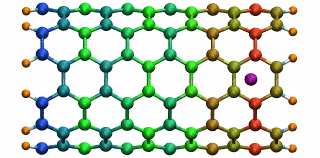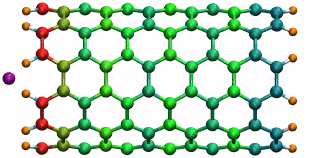  Figure 5: A potassium ion is oscillating inside a 16 angstrom long SWNT segment. (higher quality movie, 438 K)

The SWNT-K+ complex was simulated for 4.84 ps with a time step of 2 fs, employing the polarizable SWNT model. After being released 1.0 angstrom outside the SWNT with zero initial velocity, the ion is attracted by the potential well and begins to oscillate. During the simulation, the ion finished two complete oscillation cycles with a frequency of 0.43 THz. The motion of the ion naturally drags the electrons of the SWNT to oscillate at the same frequency. The oscillating motion of the ion and the fluctuation of the SWNT electrons are shown in Fig. 5 with carbon atoms colored according to their induced charges (red: negative; blue: positive). This terahertz nano-oscillator could serve as a THz wave detector which can operate at room temperature.

Publications

Publications Database The role of molecular modeling in bionanotechnology. Deyu Lu, Aleksei Aksimentiev, Amy Y. Shih, Eduardo Cruz-Chu, Peter L. Freddolino, Anton Arkhipov, and Klaus Schulten. Physical Biology, 3:S40-S53, 2006. Ion-nanotube terahertz oscillator. Deyu Lu, Yan Li, Umberto Ravaioli, and Klaus Schulten. Physical Review Letters, 95:246801, 2005. (4 pages). Empirical nanotube model for biological applications. Deyu Lu, Yan Li, Umberto Ravaioli, and Klaus Schulten. Journal of Physical Chemistry B, 109:11461-11467, 2005. Screening of water dipoles inside finite-length armchair carbon nanotubes. Yan Li, Deyu Lu, Slava V. Rotkin, Klaus Schulten, and Umberto Ravaioli. Journal of Computational Electronics, 4:161-165, 2005. Finite-size effect and wall polarization in a carbon nanotube channel. Deyu Lu, Yan Li, Slava V. Rotkin, Umberto Ravaioli, and Klaus Schulten. Nano Letters, 4:2383-2387, 2004. Electronic structure and dielectric behavior of finite-length single-walled carbon nanotubes. Yan Li, Deyu Lu, Slava V. Rotkin, Klaus Schulten, and Umberto Ravaioli. In Proceedings of the Fourth IEEE Conference on Nanotechnology, pp. 273-275, Munich, Germany, 2004.

Investigators

To Learn More About Carbon Nanotubes

Useful web links

Research groups

Page created by Deyu Lu.