Excitation Dynamics
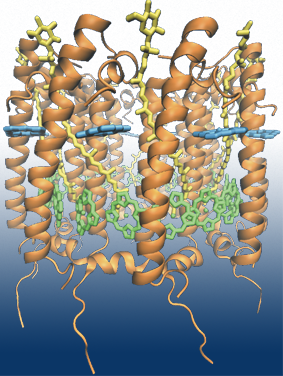 Fig 1: Light harvesting complex 2 from Rhodobacter sphaeroides contains 36
pigment molecules in total: 18 BChls in the B850 ring (in green), 9 BChls in
the B800 ring (in cyan) and 9 carotenoids (in yellow).
Fig 1: Light harvesting complex 2 from Rhodobacter sphaeroides contains 36
pigment molecules in total: 18 BChls in the B850 ring (in green), 9 BChls in
the B800 ring (in cyan) and 9 carotenoids (in yellow).
The theoretical description of excitation transfer
Excitation transfer between pigment molecules, such as bacteriochorophylls (BChls), and between pigment-protein light harvesting complexes, such as light harvesting complex 2 (LH2), has been investigated for many years using many different theoretical descriptions. Typically these descriptions include a priori assumptions about the dynamics of the system. Such assumptions are often made due to incomplete knowledge to make the system numerically tractable so that further insight can be gained. In the theoretical models of excitation transfer, it is often assumed that one parameter is much larger than another, allowing the system to be treated perturbatively. These assumptions, however, should be physically reasonable and should be tested if possible.
The description of the excitation transfer between the BChls of light harvesting complexes is particularly difficult. Excited BChls interact strongly with each other, and also with the surrouding environment. The typical perturbative approaches, namely by treating either the BChl-BChl coupling or the BChl-environment coupling as the perturbation, cannot be readily applied.
Excitation of a single BChl quickly spreads to surrounding BChls to create a coherently delocalized excitation, called an exciton. The thermal fluctuations of the surrounding protein, lipids, water and ions (i.e., the environment), however, reduces coherence. Thermal fluctations also assist excitation transfer. If the excited state energies of two BChls are very different, i.e. they have poor overlap, then thermal fluctuations broaden them and improve their overlap, thus improving excitation transfer. The contrary occurs if two BChls have very similar excited state energies.An accurate model of excitation transfer needs to be able to take both the effects of coherence and thermal noise into account. For this reason, perturbative descriptions, such Redfield theory (see Ishizaki and Fleming, J. Chem. Phys. 2009) are not valid.
Light harvesting system of purple bacteria such as Rhodobacter sphaeroides contain many well defined clusters of BChls, scaffolded into proteins such as LH2. The BChls within a cluster are typically strongly coupled to each other (with a nearest-neighbour coupling constant of ~300 wavenumbers) and also to the surrounding environment (with a reorganisation energy of ~200 wavenumbers). The coupling between clusters of BChls is, however, significantly weaker (less than 10 wavenumbers).
Testing generalized Förster theory
Historically, generalized Förster theory (Sener et al.
J. Phys. Chem. B. 2002)
has been employed to calculate the transfer rate between clusters of BChls. The
method involves the assumptions that:
(1) The equilibrium distribution of the donor exciton states
can be approximated the Boltzmann distribution of eigenstates of the effective
Hamiltonian.
(2) The equilibrium distribution arises after initial excitation on a timescale much shorter than
the excitation transfer time between donor and acceptor clusters.
(3) Coupling within a cluster is significantly stronger than coupling between clusters.
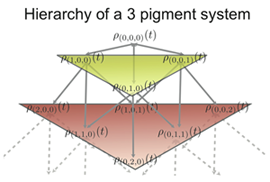 Fig 2: The hierarchy of density matrices for a 3 pigment system.
Fig 2: The hierarchy of density matrices for a 3 pigment system.Assumption (3) is readily checked by a comparison of the different coupling values. Due to the large distances between non-neighbouring BChls, their coupling can be approximated by the interaction of their transition dipoles. Using this we get that the inter-cluster coupling is an order of magnitude less than the intra-cluster coupling, enough to satisfy (3). To test assumptions (1) and (2) is not as simple and a method is neede to obey the following conditions:
- It should be non-perturbative in the inter-BChl coupling and in the system-environment coupling.
- It properly takes into account quantum coherence between BChls.
- It includes the non-Markovian behaviour of the environment.
The coupling hierarchy that arises for a system comprising of 3 pigments is shown in Fig. 2. The indices on the density matrices are a numbering scheme that keeps track of which auxiliary density matrices affect each other. The density matrix with the index (0,0,0) is the system density matrix of interest.
To investigate the validity of assumptions (1) and (2) of generalized Förster theory (see above) in the case of LH2-LH2 transfer, we calculated the excitation dynamics using the HEOM in two cases: for a single LH2 and for two LH2s in steric contact (Strumpfer and Schulten, J. Chem. Phys. 2009). In the case of one LH2 we found that the excitation in the B850 ring reaches a steady-state in approximately 1 ps (see Fig. 3). Furthermore we can reasonably approximate the steaty state using a Boltzmann distribution of eigenvalues of the effective system Hamiltonian.
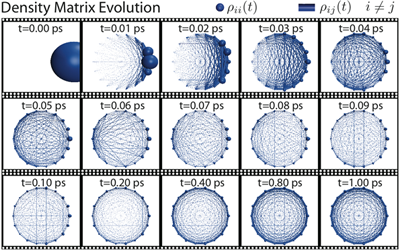
Fig 3: Pictured here is an illustration representing the density matrix evolution for the 18 BChls in the B850 ring of LH2. The diagonal terms in the density matrix are represented by the size of the spheres and the off-diagonal terms are represented by the size of the cylinders between the spheres. By 1 ps the system has reached its steady-state.
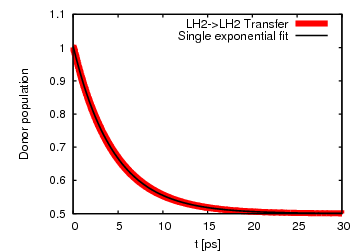 Fig 4: Excitation transfer between LH2s can be fitted by a single exponential,
indicating incoherent population transfer.
Fig 4: Excitation transfer between LH2s can be fitted by a single exponential,
indicating incoherent population transfer.For the case of 2 neighboring LH2s, we looked at the transfer from a donor LH2 to an acceptor ring of LH2. We found that the excitation transfer is completely incoherent and has a transfer time of 9.1 ps. Using generalized Förster theory the transfer time is calculated to be 10.2 ps, in good agreement with the significantly more expensive HEOM.
What about correlated environmental fluctuations?
Calculations of excitation dynamics in photosynthetic systems, including the ones described above, are often done with an additional assumption: that thermal fluctuations affect each pigment independently. Indeed, it is not simple to describe what the effect of correlated fluctuations would be. Luckily the HEOM can again be used, this time to investigate the effect of correlated site-energy fluctuations.
To include the effects of static disorder (disorder on a timescale longer than the simulation time, e.g. large-scale structural changes instead of molecular vibrations), a model system for LH2 to LH2 excitation transfer was studied. We constructed a system comprising of 4 BChls: two pairs of strongly coupled BChls, with weak inter-pair coupling (see Fig. 5).
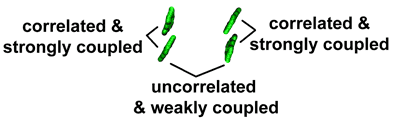 Fig 5: A model for LH2-LH2 transfer consisting of 2 BChl pairs. Each stronly
coupled pair represents a strongly coupled 18 BChl B850 ring.
Fig 5: A model for LH2-LH2 transfer consisting of 2 BChl pairs. Each stronly
coupled pair represents a strongly coupled 18 BChl B850 ring.The model system was simulated with 3 cases of correlation: perfectly
anti-correlated ("-"-correlated), uncorrelated and perfectly correlated ("+"-correlated). The resulting absorption spectra and population dynamics highlight two important findings: (1) correlation strongly affects absorption and excitation transfer and (2) the inclusion of static disorder has a much stronger effect when dynamic fluctuations are correlated (Strumpfer and Schulten,
J. Chem. Phys., 2011). Figure 6 shows the effect of correlation and
static disorder on the absorption spectrum and on excitation transfer.
It seems that it is better to have uncorrelated fluctuations in the presence of static disorder for optimum excitation transfer. It has also been
demonstrated that the excited state fluctuations of the BChls in LH2 may indeed uncorrelated (see Olbrich and Kleinekahoefer J. Phys. Chem. B, 2011). Indeed, nature may have evolved this way to improve excitation transfer efficiency.
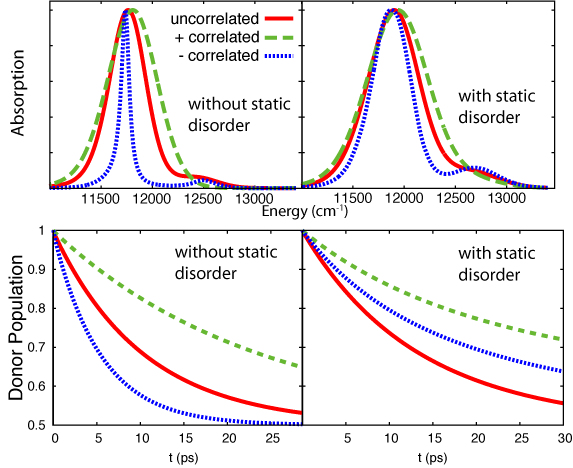
Fig 6: Absorption spectrum of and excitation transfer between strongly coupled BChl pairs with perfectly correlated fluctuations, uncorrelated fluctuations and perfectly anti-correlated fluctuations)
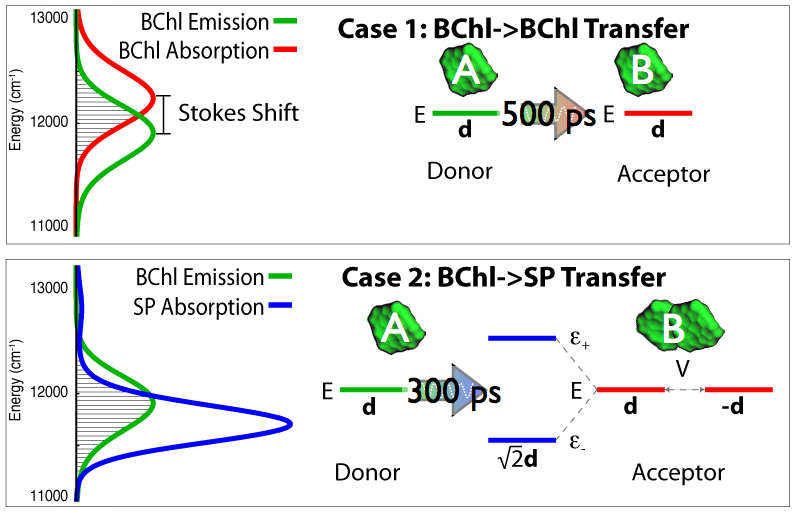
Fig 7: Quantum coherence modifies the excited state energy levels and combines transition dipole moments of the
pigments in purple bacteria, thus enabling the required transfer of excitation over large distances.
The role of quantum coherence
After the surprising observation of quantum mechanical effects in photosynthetic pigment-protein complexes in purple bacteria (Lee et al.,Science, 2007) there has been much interest in what role quantum coherence may play in photosynthetic light harvesting. Indeed, quantum coherence between pigment molecules have been theoretically described earlier (Hu et al., J. Phys. Chem. B, 1997). More recently, we have written reviews detailling the description of excitation tranfer in photosynthetic systems aimed at undergraduates (Strümpfer et al., The light-harvesting apparatus in purple photosynthetic bacteria, introduction to a quantum biological device., 2011) and clearly showing how quantum coherence benefits light harvesting in purple bacteria (Strümpfer et al., J. Phys. Chem. Letters., 2012). The effect and benefit of quantum coherent sharing of excitaiton is shown in Fig 7.
Publications
Investigators
Related TCB Group Projects
Page created and maintained by Johan Strumpfer.