Organization of energy transfer networks in photosynthesis
Photosynthesis is the primary energy source for most of the biosphere. Even though photosynthetic light harvesting complexes display great variety in their design and function, many of them are membrane proteins that comprise of pigment antenna arrays which absorb light and transfer the resulting electronic excitation to a reaction center which in turn converts this excitation energy to a charge gradient across the membrane.
Drive towards complexity
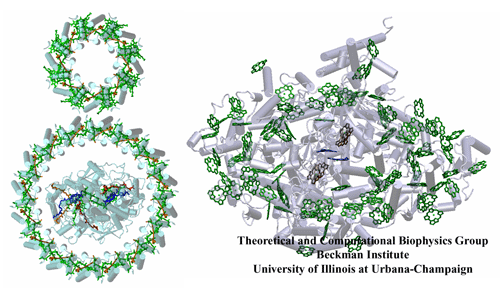
It is of interest to compare anoxygenic light harvesting mechanisms to oxygenic ones. Purple bacteria, which perform anoxygenic photosynthesis, feature the oldest known light harvesting apparatus, while the oxygenic cyanobacteria, plants and green algea are evolutionarily more recent. In a purple bacterial photosynthetic unit pigments form highly symmetric ring-like structures (see figure). In contrast, the pigment network of photosystem I from oxygenic species forms a rather random looking array with a higher packing density of chlorophyll per unit mass. In fact, photosystem I and its associated complexes display a greater complexity in plants as compared to cyanobacteria as discussed in the tale of two photosystems.
A comparison of anoxygenic and oxygenic light harvesting mechanisms. (left) A sample photosynthetic unit (PSU) of purple bacteria: a peripheral light harvesting complex LH2 (small ring) funnels its harvested light energy to an LH1 complex (big ring) which in turn delivers its energy to the reaction center it surrounds. There might be up to around ten LH2's per LH1 in a PSU. (right) Photosystem I from cyanobacteria combine the peripheral antenna array, the reaction center, and the electron transfer chain in to a single protein.
The circular arrangement of pigments found in purple bacteria seems to be a consequence of simple assembly and aggregation requirements rather than having a specific functional role, since the effects of thermal disorder erase any symmetry artifacts that would be left over if the system were to function at cryogenic temperatures. This raises the question of whether the more closely packed and seemingly random chlorophyll network, found in cyanobacteria and plants, serves a particular functional role or whether it can be safely regarded as a 'random bag of chlorophylls'. Are there overarching organizational principles for the geometry of chlorophyll networks? In order to address this question the kinetics of the excitation migration process, which takes place in a picosecond time scale, needs to studied in some detail.
From structure to function
The physics of the excitation migration process is fairly well understood and is described to a reasonable approximation by Foerster theory within the context of an effective Hamiltonian formalism (Sener et al. 2002a). This framework enables one to construct, from structural information regarding cholorophyll position and orientations such as provided by the work of our collaborator Petra Fromme, the geometry of an excitation transfer network as well as stochastic formulations for the measurable quantities of the excitation transfer process such as the average excitation lifetime or the overall quantum yield. (Quantum yield is the probability with which the energy of an absorbed photon is utilized for charge transfer as opposed to being lost to thermal dissipation.) Remarkable agreement between the computed timescales and quantum yields with observed ones indicate that the fundamentals of the excitation migration are understood at least to some reasonable degree.
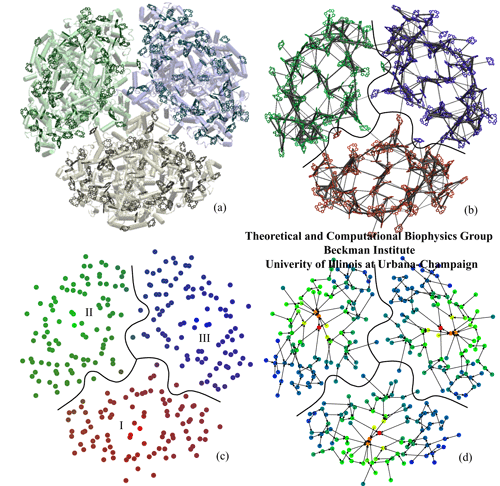
Four ways of looking at the chlorophyll network of the photosystem I trimer. (a) The protein--pigment complex (cofactors other than chlorophylls not shown). (b) Excitation transfer rates between individual chlorophylls. The thickness of a bond between two chlorophylls is proportional to the logarithm of the transfer rate between them. For simplicity, only the largest rates are shown. (c) Connectivity between different monomers. The measure is given by the probabilities of charge transfer from a given reaction center for an initial condition corresponding to a perfectly localized excitation at a given chlorophyll. The content of red, green, and blue are proportional to the probability of charge transfer from the bottom, left and right reaction centers, respectively. (d) Representative pathways of excitation migration. The arrows between chlorophylls characterizing the migration are assigned according to a steepest-descent criterion based on mean first passage times to the reaction center. The colors denote increasing mean first passage times from red to blue. (Sener et al. 2004a).
However, an analysis of the light harvesting function based on the frozen geometry of an atomic structure is not a sufficient description for a system that functions at physiological temperatures.
Thermal disorder
The processes of photon absorption, excitation migration and electron transfer are all fundamentally quantum mechanical in nature. Since these processes occur at finite temperature, a satisfactory description of the light harvesting function needs to account for the effects of thermal disorder in a quantum mechanical system.
Random matrix theories, widely employed in condensed matter physics and high energy physics, provide a framework within which thermal effects can be formulated in terms of ensemble averages over a space of random Hamiltonians. This enables one to employ field theory methodologies for finding elegant and succint descriptions, for example, for spectral properties of a light harvesting complex at nonzero temperatures (Sener et al. 2002b, Sener et al. 2002a).
The theoretical framework outlined so far can now be used to compare various chlorophyll network geometries such as ones that arise from thermal fluctuations, external perturbations (such as loss of a chlorophyll), or a competitive new design of a neighboring species. How much change can a chlorophyll network take and still survive?
Hard life to live: surviving thermal disorder, environmental change and competition
Survivability. What is a good quantitative measure for survivability? What are the most important evolutionary pressures that a species has to contend with?
Environmental change and competition are two major challenges that all biological systems must cope with. Adaptability to changing external conditions, or robustness, of a system typically manifests itself in terms of a parameter insensitivity of its dynamics and a graceful degradation of its components. Competition, on the other hand, drives a system towards optimality, as a less efficient system will find itself at an evolutionary disadvantage.

Adaptive and competitive pressures of evolution drive a species toward tolerance to change, i.e. robustness, on the one hand and toward high relative efficiency, i.e. optimality, on the other.
It is very difficult to quantify robustness and optimality in general terms for an arbitrary biological system since the fitness landscape over which adaptability needs to be judged is enormously complex. A light harvesting system, however, provides a natural, if somewhat crude, measure of its efficiency in terms of the quantum yield of the excitation migration process.
It is a simple matter to model the effects of various perturbations, such as thermal disorder or loss of individual components, on the quantum yield within the theoretical framework outlined above. Similarly, questions regarding the optimality of the geometry of the chlorophyll network can be investigated by generating ensembles of alternative network configurations. (Sener et al. 2005).
Quantum yield of a light harvesting system as a (crude) measure of fitness
The quantum yield of a light harvesting system is typically very high. It is given by a near unit probability, as most every photon absorbed by the chlorophyll network results in an electron transfer. Strangely, this no longer remains true at cryogenic temperatures, where quantum yield drops significantly and becomes dependent on the wavelength of the incident photon. This results from the loss of spectral overlap necessary for resonant energy transfer between donor and acceptor chlorophylls that may have different energies. (Having all pigments to have the same energy would have solved the resonance problem at any temperature, but then only a tiny window of the spectrum would be covered by the pigment array, save for spectral broadening due to excitonic coupling.) Thus, thermal disorder actually helps to maintain a high quantum yield by broadening cholorophyll spectral lineshapes and enabling resonant energy transfer even with some energy separation between chlorophylls.
A study of quantum yields in an ensemble of randomly generated chlorophyll network geometries show that the high quantum yield of the system remains manifest under thermal fluctuations of chlorophyll orientations, chlorophyll site energies, as well as even loss of individual chlorophylls from the network. Thus, there is a degree of robustness present in such a chlorophyll network as quantified by the quantum yield.
However, within this narrow range of quantum yields for random geometries it is seen that the original configuration, as given by the geometry corresponding to the crystal structure, is nearly at the top of the distribution (Sener et al. 2004a).
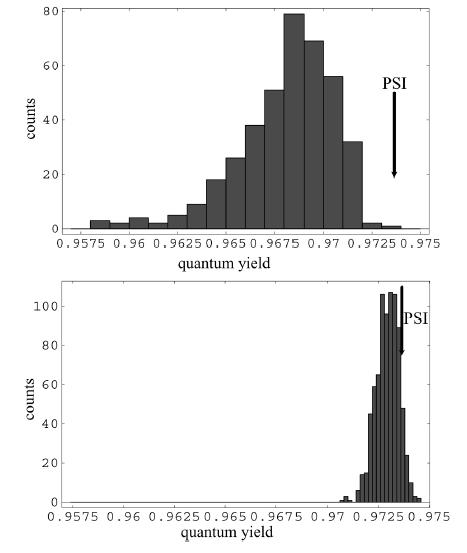
High relative quantum yield as a sign of optimality. Histograms of quantum yield are shown within an ensemble of random chlorophyll reorientations. The quantum yield of the original geometry given by the known atomic structure is indicated by an arrow. (top) All chlorphylls randomly reoriented, including reaction center chlorophylls. (bottom) Six reaction center chlorophylls kept fixed while the rest are randomly reoriented.
The high relative quantum yield of the original geometry within an ensemble of random configurations can be regarded as a sign of optimality. However, this raises the question of whether a quantum yield increase of a fraction of percent is of any importance for the survival of a species. It is unlikely that for the day-to-day functioning of a light harvesting complex such a tiny change will be noticable, but over evolutionary timescales the cumulative effect of a slightly better efficiency can be a discriminating factor, as suggested also by growth competition experiments,
It must also be kept in mind that excitation transfer is not a rate limiting step for the overall light harvesting process, therefore its efficiency as given by the quantum yield can provide only a crude and incomplete measure for fitness. It still remains a challenge today to formulate other quantitative measures for the robustness and optimality of a light harvesting system that are still computationally tractable.
Related Projects
- The Tale of Two Photosystems
This page continues our story within the context of a comparison of plant and cyanobacterial photosystem I complexes revealing some of the principles that shape the evolution of the chlorophyll network. - Quantum Biology of the Photosynthetic Unit
- Light-Harvesting by Carotenoids
Publications
Investigators
- Melih Sener
- Deyu Lu
- Sanghyun Park
- Ana Damjanovic
- Thorsten Ritz
- Petra Fromme
- Klaus Schulten