Analysis Tools for MD Simulations

Teraflop computing will permit biomolecular simulations of larger systems and longer time scales, but the increased computing power should also be invested to improve the analysis of simulations, as well as to improve their statistical significance. The Resource for Biomolecular Modelling and Bioinformatics has developed the molecular dynamics program NAMD2 that takes advantage of massively parallel computers and it has already gained much experience with teraflop scale simulation projects. The Resource wants to develop now for such projects a library of Molecular Modelling Tools, MMTools, that monitor physical characteristics of simulated systems, and analyze them in the framework of advanced statistical mechanics. MMTools will be an extendable library of modular routines (written in C++, like NAMD2), which can be invoked by the user through Tcl scripts. The user will have the option to (1) analyze and process on-the-fly the relevant data of a molecular dynamics run, by invoking MMTools via the Tcl scripting capability of NAMD2, or (2) use MMTools to process and analyze completed molecular dynamics simulations. An electronic textbook will be provided that explains the concepts and specific tools as well as illustrates MMTools through examples.

1 Introduction

The Resource for Biomolecular Modeling and Bioinformatics proposes to establish a library of analysis and data processing tools, hereafter referred to as Molecular Modelling Tools (MMTools), for molecular dynamics (MD) simulations. MMTools will be needed because of the increased scope of MD simulations in the era of teraflop computing. Such simulations will cover orders of magnitude longer times and larger system sizes, and permit better sampling; this provides an opportunity to improve the statistical significance of simulations. The power of teraflop machines can also be used to calculate a more extensive set of physical characteristics for a simulated system.

MMTools will consist of an extendable set of modular routines, written in C++. The routines will be accessible via a standard Tcl command language script, provided by the user. A Tcl interface will link MMTools to the molecular dynamics program NAMD2 ¹ developed at the Resource, which will permit the user to invoke MMTools during an NAMD2 session for on-the-fly monitoring and analysis. Through Tcl scripts, the user will also have the option to employ MMTools for processing MD data of simulations completed with NAMD2 or any other MD program.

Initially, MMTools will comprise the following ten tools: (1) correlation functions - for calculating equal-time-, auto- and cross-correlation functions; (2) principal component analysis - for identifying and characterizing slow modes in proteins; (3) linear response theory - for investigating the response of a biomolecular system to an external weak perturbation; (4) hysteresis - for analyzing the nonlinear and time-delayed response of a system to a periodical external perturbation; (5) echoes - for studying the coherent excitations of protein modes via consecutive sudden perturbations; (6) time series analysis - for reaction coordinate analysis and for reconstruction of potential of mean force (PMF); (7) mean first passage time analysis - for describing potential barrier crossing events; (8) spin-boson model - for modeling spectral line shapes and (potential) curve crossing phenomena in proteins; (9) vector quantization of protein dynamics - for determining topologically discrete representations of manifolds covered by protein dynamics; and (10) a test suite - for testing the functionality and performance of the currently available MMTools for three sample systems of different size, i.e., a small protein (1000 atoms), a medium protein-water system (10,000 atoms), and a large protein-lipid-water complex (100,000 atoms).

As already mentioned, MMTools can be readily linked (via Tcl) by the user to an NAMD2 run. Moreover, the user can check the sampling of data during runtime using the BioCoRE² monitoring tools provided for NAMD2. At certain intervals the tools carry through the computational analysis in terms of physical characteristics like correlation functions, response functions, running averages of physical observables, etc., providing a run time view of the various characteristics.

The analysis is based to a large degree on concepts from non-equilibrium statistical mechanics that are conceptually and mathematically demanding and unfamiliar to many investigators. For this reason a detailed tutorial in the form of an electronic textbook will be developed that explains the physical theory behind MMTools and illustrates its use through examples.

MMTools will be distributed along with all software of the Resource through the web³. The use of MMTools will be evaluated both for projects carried out at the Resource and for user projects. Workshops on the use of Resource software will include introductions into the use of MMTools.

2 Background and Significance

Molecular dynamics simulations and molecular modeling are today essential research instruments in biomedicine that complement observation, permit rational approaches in design of experiments, provide access to complex data and models, and yield atomic level understanding of cellular processes. The development of these instruments were closely tied to advances in computing technologies, starting with the DEC 780 providing main frame computer power in the molecular biology laboratory to the recent Cray T3E that permits routine nanosecond simulations of fully solvated proteins.

Presently, technology promises another great advance in computing power towards teraflop and even petaflop speeds employing very large parallel machines. On this new generation of computers, simulations can be carried out for systems thousand times larger or over time scales thousand times longer than previously, permitting the study of protein-protein and protein-nucleic acid recognition and assembly, the investigation of integral functional units of cells, e.g., eventually a complete ribosome, and bridging the gap between computationally feasible and functionally relevant time scales, e.g., for protein folding.

One hopes that the advances through teraflop and petaflop computing will also improve the quality of molecular modeling through the better statistics stemming from larger system size and longer time scales as well as through increasing, if necessary thousand fold, the sample size of simulations where previously conclusions were based often on single simulation runs. One also hopes that the increased computer power will serve to monitor simulations better, collecting in the course of runs all key physical attributes that pertain to biological function. But to realize these hopes requires actually a considerable investment in program development that is beyond the capacity of most biomedical researchers involved in molecular modeling. The challenge is particularly great in the present case since the needed tools stem from the field of non-equilibrium statistical mechanics, a rather advanced subject that is not taught in most curricula.

Figure 1: Schematic structure of MMTools. The three main components of MMTools are (i) a collection of Analysis Tools, (ii) a Routine Library, and (iii) a Tutorial with Examples on how to use MMTools. A Tcl interface will allow MMTools to communicate with the other molecular modeling software of the Resource, namely NAMD2 and VMD.

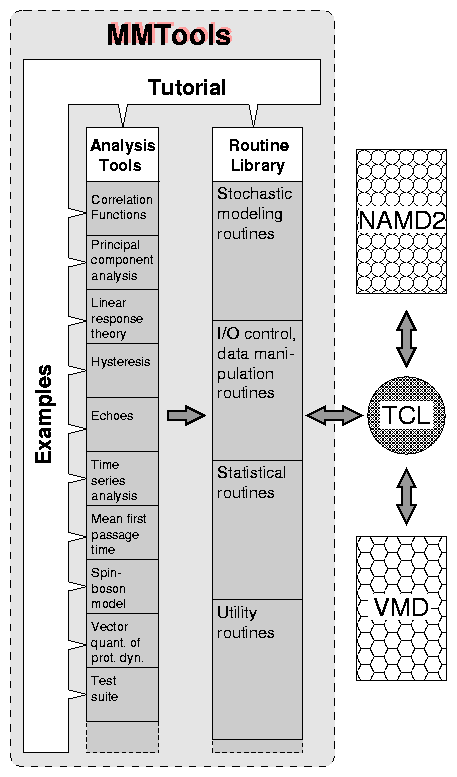
The Resource is in an excellent position to contribute to the development of the needed physical analysis tools, MMTools, and their employment. As summarized in Fig. 1, three aspects of its past efforts provide an ideal starting point for MMTools, namely, the architecture of the Resource's modeling program NAMD2, the expertise from past projects, and a considerable investment into a tutorial text through the teaching and dissemination efforts at the Resource. NAMD2 has been designed to work with Tcl scripts that can control simulations. In the present case this permits that MMTools is provided in the form of a library of routines (written in C++) which can then be invoked by NAMD2 via a Tcl script. During the past decade, the Resource has already developed tools based on non-equilibrium statistical mechanics for a broad range of simulation systems and tasks. This experience furnishes now a basis to turn ad hoc solutions of the past into a library of systematic tools. Lastly, the Resource has developed a course at the Physics Department of the University of Illinois at Urbana-Champaign, taught since several years, that lead to an electronic textbook⁴ which can now be readily extended into a tutorial for MMTools.

The need for monitoring and analysis tools are illustrated below for three examples.

(1) Structure-function relationship of the purple membrane in Halobacterium salinarium.⁵ - The system studied involves a hexagonal, two-dimensional crystalline array that exists in the cell wall of some halobacteria with a very small lipid content and a single protein component (bacteriorhodopsin). The purple membrane absorbs sun light and converts it into a proton-motive force across the membrane, switching its proton pumping acticity off when the potential exceeds about 200 mV. The project at the Resource combined crystallographic data from various groups to develop a complete structural model of the purple membrane that comprises all protein and lipid components with few uncertainties [1].

NAMD2 constant pressure (NpT ensemble) simulations with full electrostatics and periodic boundary conditions for non-orthogonal cells (23,783 atoms) are presently carried out. In order to explain the purple membrane's mechanism a key characteristic, the tight electrostatic coupling between the system's chromophore retinal and the protein, must be investigated. This requires the calculation and monitoring of (i) excitation energy time series, (ii) various overall dipole moments, (iii) correlation and response (e.g., dipolar response) functions, (iv) spectral line shape functions, (v) specific heats, and (vi) thermodynamic potentials of internal water molecules to establish the role of the latter in proton translocation. The MMTools components needed for this set of analyses are: correlation functions, linear response theory, hysteresis, time series analysis.

(2) Atomic force microscopy and steered molecular dynamics simulations of proteins in the extracellular matrix.⁶ - Extending a successful project at the Resource on the molecular mechanism of the muscle protein titin that involved collaborations with experimental researchers at U. Washington, Seattle, and Mayo Clinic, Rochester, the investigators are embarking now on the study of fibronectin and proteins of the immunoglobulin superfamily that interact with integrins and trigger cellular responses in the extracellular matrix[2].

The simulations need to relate protein architecture and mechanical properties controlled through side group packing, hydrophobic core interactions and hydrogen bonding to mechanical properties that protect proteins from unfolding and provide tensil sensory action, e.g., through the RGD loop in fibronectin. The simulations need to monitor time series of conformational and energetic properties as well as of applied forces; an analysis of these data should yield correlation and response functions, thermodynamic potentials and other properties. Needed MMTools components are: time series analysis, mean first passage time analysis, correlation functions, hysteresis.

(3) Ion selectivity of the KscA potassium channel.⁷ - The potassium channel KscA in Streptomyces lividans exhibits high selectivity for potassium over sodium ions while maintaining very high conductivity levels. The channel, recently structurally resolved, is found to be closely related to potassium channels in cells of many species and, hence, an explanation of its selectivity and control is highly desirable. A project at the Resource has established a model of the channel in an intact PEPG bilayer-water system using NAMD2 in NpT ensemble mode with periodic boundary conditions and full electrostatics. The project involved steered molecular dynamics, applying external forces in order to accelerate the conduction process. This technique requires monitoring of the time series of the applied force and ion velocity as well as position in order to abstract the potential of mean force governing conduction. The method permits studying the system dynamics actually in a higher dimensional setting that accounts for the concertedness of ion, water and protein motion. The method corresponds closely to the WHAM approach to umbrella sampling, except that it permits the analysis of non-equilibrium situations [3]. The required components of MMTools are: time series analysis, correlation functions, principal component analysis, mean first passage time analysis.

These projects and others at the Resource illuminate essential needs of monitoring and analysis tools. The following list summarizes tools that are lacking today in many cases and that biomedical researchers require for the type of projects described. References provided below demonstrate the previous efforts of the Resource, but furnish information on the important contributions of other researchers only indirectly through the citations found in the given references.

Correlation functions, e.g., velocity correlation functions [4] or energy correlation functions, characterize dissipative processes or redox processes [5,6,7]; position and force correlation functions yield information which identifies soft modes of proteins [8].

Principal Component Analysis describes major motions of proteins that might be functionally relevant, e.g., fluctuations describing gate opening and closing in ion channels. Large scale motions of proteins are typically not revealed in crystallographic structures, but might be deducible from them through long time simulations when properly analyzed [8]. Algorithms are usually based on diagonalizing position or force correlation functions, but there exist also methods that permit the determination of large amplitude motions without sampling and diagonalizing correlation matrices beforehand, rather gathering information on-the-fly [9,10].

Linear response theory. The fluctuation-dissipation theorem (FDT), that holds in the limit of linear response theory, states a relationship between many correlation and response functions. This relationship can be exploited to either avoid the calculation of response functions (that require perturbations in separate simulations) or to provide a consistency check of simulation runs when both correlation and response functions have been gathered. The FDT has been successfully applied in several instances, e.g., in the study of electron transfer in proteins (e.g., photosynthetic reaction center [5,6]), or the response of a protein to external electric fields[11].

Hysteresis. Hysteresis is a phenomenon that accompanies all cyclic processes in proteins, but can also serve as a probe when cyclic conditions are artificially enforced, e.g., through oscillatory fields or periodic forces in atomic force microscopy. The phenomenon reveals basic physical properties, e.g., frictional elements, as well as non-linear couplings underlying a process. A systematic theory has been developed only recently, the Resource having contributed both conceptually and technically [12,11].

Echoes. Velocity replacement [13] and temperature quench [14] echoes probe the coherent motion in proteins with phase relaxation times of about 1 ps. The methodology is based on a set-up that can only be realized numerically, limiting somewhat the relevance of the approach. However, echoes provide presently the only model-free method to address the long-standing problem of coherent vibrations in proteins [15].

Time series analysis. Steered molecular dynamics simulations manipulate biomolecular systems through the application of (multi-dimensional) forces F(t) that lead to responses as measured, e.g., through conformational transitions captured by x(t) [16,17,18,19,20,21,22,23,24,25,2]. Analysis of the resulting time series {F(t), x(t),v(t)}, corresponding to the manipulated biomolecular system, in terms of stochastic models can yield certain attributes, e.g., thermodynamic potentials, potentials of mean force (PMF), binding affinities, or reaction barriers [26,3,27]. A most important application is reaction coordinate analysis: in this case steered MD simulations select either intuitively or by some systematic method a reaction coordinate for a process of interest; the system is then ``pulled'' along this (possibly multi-dimensional) reaction coordinate; the behavior of the system is finally monitored and analyzed through the time series analysis method. The desired results are the reaction coordinate, diffusion coefficient D and friction coefficient g along the coordinate, as well as the PMF [26,3].

Mean First Passage Time Analysis. This method combines several trajectories from steered molecular dynamics simulations governing a barrier crossing or other events characterized through first passage times[27]. The distribution of passage times monitored, in combination with a stochastic model, permits one to deduce model characteristics, e.g., height and shape of reaction barriers.

Spin-boson model. The spin boson model describes the coupling of a two-state quantum system, as encountered for example in an optical transition or in a redox process, to a protein described as a collection of harmonic oscillators[28,7,29,30]. The characteristics of the coupling can be derived from correlation function properties and certain distributions. The spin-boson-model, widely applied in physical and biological theory, furnishes then the spectral line shape function and its temperature dependence and, hence, rates of optical or electron transfer events (assuming that the electron coupling is known).

Vector quantization of protein dynamics. This is an algorithm for topologically faithful discrete representations of manifolds [31,32], e.g., those covered by protein dynamics. The algorithm allows one to sample protein motion and to represent the result through a discretized space that is optimally matched to the sample. This permits one to sample the phase space of a protein to identify reaction paths or conformational distributions. The method yields also a multi-resolution analysis of protein structures that allows one to combine crystallographic, electron microscopy, and modeling data [33].

Test suite. For the testing of molecular dynamics simulations using widely different simulation schemes a representation in terms of trajectory data is unsuitable. One rather wishes to represent simulations through the key physical properties of a modeled system, e.g., correlation and response functions, as well as, thermodynamic and relaxation properties. A test suite within MMTools will be developed covering a small (1000 atoms), a medium (10,000 atoms), and a large (100,000 atoms) system, as described above. An extensive set of calculations will be carried out on these systems and thermodynamic data taken. Future simulation methods can use this test suite to check if properties are properly reproduced in new types of algorithms and modeling approaches. The test suite will be also used on other MD programs, e.g., Charmm⁸ and Amber⁹.

3 Preliminary Studies

The Resource has continuously demonstrated the ability to successfully apply advanced computational technology to a wide range of challenging problems in structural biology. The Resource has established a leadership role in large scale simulations, as is evident from the record of completed and published applications [34,35,36,37,25]. Resource researchers invested their efforts in advanced software, novel algorithms and state-of-the-art hardware. The software developed is freely available to the biomedical community and is widely distributed.

We have taken a broad approach, reflected in the development of (1) NAMD2, a parallel, object-oriented molecular dynamics program, designed for high-performance simulation of large biomolecular systems [38], (2) VMD ¹⁰, the Resource's popular molecular graphics program [39], and (3) BioCoRE, the Resource's integrated, tool-oriented computing and communication system to support collaboration in the field of structural biology [40].

The computational and graphics laboratory of the Resource is unsurpassed amongst academic biomedical institutions. To a large extent, the success achieved can be attributed to the multidisciplinary approach taken by investigators from departments of computer science, physics, chemistry and biophysics.

The Resource was among the first groups in structural biology to see the promise of parallel computer architectures [41,42,43,44,34,45]. These new architectures require programming techniques and concepts which can be very difficult to retrofit in code originally meant for serial execution. We have also implemented several state-of-the-art algorithms in NAMD2, which are applicable in both serial and parallel computing environments, and enable users to perform ever-larger and longer simulations. For example, we incorporated the fast N-body solver DPMTA [46], making it practical to include full effect of electrostatics into MD simulations. We also developed and implemented the multiple time scale integration method Verlet-I [43], also known as reversible RESPA [47], which has greatly improved simulation performance. NAMD2 has been designed as a flexible program, incorporating many options to control integration methods, force field parameters, etc. NAMD2 is user friendly and is easy to modify and extend to serve goals we have not foreseen. This modifiability is accomplished in NAMD2 through extensive documentation at both user and programmer levels, and free availability of source code written with an object-oriented design. NAMD2 is unique in the extent to which other researchers can transform it to perform specific tasks. Via its Tcl scripting language capability NAMD2 can easily be interconnected with other Tcl based client applications. MMTools will exploit this unique feature of NAMD2 providing, thereby, on-the-fly data analysis and processing capabilities.

VMD is a mature visualization environment for structural biology. Many research groups have adopted VMD for plain visualization, for docking studies, structure refinement, trajectory analysis, and interactive dynamics [48]. Recently added capabilities include enhanced flexibility in display options, extensions to the scripting language, static docking, and structure alignment. Through the enhanced scripting language, new analysis routines may now be written without recompilation of VMD. The improved scripting language allows nearly all mouse actions to be logged to a script file, edited, and replayed, making it easy to produce tutorials or high-quality movies. VMD runs on all major platforms, including Windows.

In supporting their various projects, researchers at the Resource have made fundamental contributions to the physical analysis of MD simulations.

Resource researchers had pioneered the use of the correlation function methods to study relaxation processes in biopolymers, such as proteins. Already twenty years ago, they used the velocity auto-correlation function in studies aimed to demonstrate that MD simulations, and their stochastic extensions, provide a consistent picture of protein dynamics over a wide range of time scales [4]. Other relevant, and very important, contributions of the Resource researchers include the following: the theory of first passage times [49,50] and general moment expansion [51] to describe molecular relaxation processes; the theory of spin chemistry and magnetic field effects that had been based on new theories of stochastic quantum mechanics [52,53]; the development and use of stochastic quantum dynamics for redox processes, in particular, the spin-boson approach [28,7,29]; the development of the theory of hysteresis [12,11]; the development of time series analysis generalizing umbrella sampling approaches to non-equilibrium manipulations [26,3]; the development of some of the first neural network algorithms, e.g., for principle component analysis [9,10] and for the representation of complex manifolds [54,32]; and, finally, contributions to the principle component analysis of MD simulations through its investigation of the sampling issues involved [8].

4 Research Design and Methods

In general, MD programs offer very limited analysis capability for the simulated data, perhaps because it is assumed that the user will be able to determine and reconstruct various quantities and properties of interest of the simulated system from the saved (position and velocity) trajectory files, and energy and temperature outputs. However, in the age of teraflop and petaflop computing the size of the simulated biomolecular systems, as well as, the length of the simulations will gradually become so large that saving complete trajectory files will require prohibitively large processing and analysis time, and disk space for storage. Moreover, since the main goal of MD simulations of biopolymers, with complex dynamics that span a wide range of time scales, is to understand their functions, one needs a systematic and extendable set of analysis tools. Currently such analysis tools are lacking in a readily accessible library format in the biomedical community, and MMTools is intended to fill this gap.

4.1 MMTools Overview

As shown in Fig. 1, MMTools will have three interconnected components: (1) the Analysis Tools, (2) a Routine Library, and (3) a Tutorial with Examples. Here, we present a brief overview of these components, while further details will be provided in the following subsections.

(1) Analysis Tools - represent the core of MMTools, and their functions have already been described in Secs. I,II. Each tool will consist of a package of complex, interrelated procedures, designed to address a specific class of problems in molecular modeling. The design and development of the algorithms on which these procedures are based, will represent a key part in the development of MMTools. The procedures will be written in C++ and will be implemented as Tcl commands via the extension mechanism of the latter. Thus, well defined input, output and control parameters will make these procedures flexible to be invoked either directly, as stand alone commands in a Tcl interpretor/script, or by inclusion into a user provided code.

(2) Routine Library - will consist of a collection of specialized subroutines and functions (Sec. IV B), which will be used by the more complex Analysis Tools. Initially, the Routine Library will comprise four classes of routines (see Fig. 1) intended for (a) stochastic modeling, (b) input/output control and data manipulation, (c) statistical data analysis, and (d) useful numerical calculations (e.g., numerical integration and derivation). These routines and functions will constitute the building blocks of the more complex procedures in the Analysis Tools.

(3) Tutorial with Examples - will explain the theoretical basis of MMTools, and will provide guidance on how to use these tools via suitably chosen examples (IV C). The tutorial will consist of an electronic book, distributed via the WWW. Each component of MMTools will be described in a separate chapter, starting with a presentation of the physical principles on which the component is based, followed by the description of the algorithms, implementation and invocation of the tool. Finally, the usage and features of the tools will be illustrated by applying them to concrete examples selected from published and ongoing research work performed at the Resource.

MMTools will be designed to take advantage of the Tcl interface built into both NAMD2 and VMD. This will make possible the communication and interaction between these programs and MMTools, allowing for on-the-fly analysis of the MD simulation results, and for a certain degree of control of an NAMD2 session via MMTools.

4.2 MMTools Routine Library

MMTools will be built on a set of specialized subroutines and functions which initially will be grouped according to their purpose and functionality in the following four groups.

(a) Stochastic modeling routines - will be used for stochastic modeling and analysis of biomolecular systems studied via MD simulation. The need for such a package of routines and their importance can be easily understood by recalling the fact that in most cases, the analysis of the MD simulation of a biomolecular system focuses usually on small subsets of relevant degrees of freedom, while the rest of the system is treated as a stochastic environment. Then, the selected subsystem is described by a suitable stochastic model, the dynamics of which is governed by a stochastic differential equation, and the equation of motion for the corresponding probability density (i.e., the Fokker-Planck equation). In general, the action of the stochastic environment on the studied subsystem can be described by an effective potential of mean force (PMF), and a stochastic Langevin force. The evaluation of PMF using MD simulation results represents a challenge for the molecular modeling community. There are several stochastic processes which can be used for modeling the dynamics of selected parts of a biomolecule. For example, the Wiener process describes free Brownian motion, while the Ornstein-Uhlenbeck process is an extension of the Wiener process in the presence of a linear drift term. Similarly, Kramers equation, a special form of the Fokker-Planck equation, represents the equation of motion of the position and velocity dependent probability distribution function in the presence of an external potential. In the large friction limit, applicable to most biomolecular processes, Kramers equation becomes the somewhat simpler Smoluchowski equation.

The set of stochastic modeling routines will contain the following:

Stochastic differential equation solver for user specified initial and boundary conditions, and for stochastic Langevin forces drawn either from several most commonly used distributions (e.g., Gaussian white noise) or from the data collected via single or multiple MD sessions.
Fokker-Planck equation solver for user-specified initial and boundary conditions, diffusion matrix and drift vector.
Kramers and Smoluchowski equation solver for user specified initial and boundary conditions, and parameters (friction coefficient, external force or potential, etc.)
Discrete and continuous master equation solver for jump processes.

(b) I/O control, and data manipulation routines - will control the data and command transfer to and from NAMD2 via a Tcl interface. The researcher will have the possibility to instruct NAMD2 on how and when to collect and output the data after a specified number of MD simulation time steps. For example, let us assume that the researcher wants to study and record the time evolution of the configuration energy along a certain reaction pathway. To this end, the researcher must instruct NAMD2 for a simulation underway when to start calculating the configuration energy, which set of atoms should be selected for this purpose, which formula should be used for the calculation, with what frequency should the data be calculated, in which file, in what format and with what frequency should the data be written on the hard disk, and, finally, under what conditions should this operation be terminated. All these tasks will be accomplished by passing a proper Tcl script (containing commands from this set of routines) to the Tcl interpretor built into NAMD2.

Another important application of the I/O control routines will be to assist the researcher in setting up, and automatically launching, multiple MD simulation sessions for better sampling. For example, once the system reaches thermal equilibrium, the researcher, by invoking a Tcl command, can automatically launch new NAMD2 sessions with initial configurations provided by the running simulation at predetermined instants of time. The individual simulations can then be monitored via Tcl commands launched simultaneously with the corresponding NAMD2 sessions by the same original Tcl command. Such an approach will increase dramatically the data collection and analysis of multiple MD simulations, resulting in much better statistics of the collected MD data.

Under normal conditions, NAMD2, like many other MD programs, outputs the results of the simulation in DCD trajectory files. A post-simulation analysis of the coordinate and/or velocity DCD files requires a DCD reader/decoder. The data manipulation library will contain such reader/decoder with very useful options, e.g., allowing the researcher to extract, on the fly, from the full trajectory file only a subset of the data, by specifying certain groups of atoms, or number of time frames to be skipped.

A subclass of I/O control routines will be designed to interface MMTools with the Tcl interpreter built in VMD. For researchers, the ability of visualizing in real time those aspects of an MD simulation they are interested in, will enhance significantly the quality of their MD data analysis. Clearly, the interconnectivity between MMTools, NAMD2 and VMD (see Fig. 1) will provide biomedical researchers with an extremely powerful and, at the same time, flexible and easy-to-use molecular modeling environment.

The initial set of I/O control and data manipulation routines will be continuously extended with new routines and functions in order to increase the quality and performance of the interconnectivity between MMTools and NAMD2/VMD.

(c) Statistical routines - will perform basic statistical processing of the data collected during an MD session, and are required by all data analysis tools. Collections of functions and subroutines for numerical statistics are readily available in both commercial (e.g., the well known NAG and IMSL scientific routine libraries) and freeware (e.g., the Numerical Recipes [55], and the SLATEC library [56]) form. Also, the statistics package in Mathematica [57] provides (via MathLink) a great collection of statistics functions. Thus, the implementation of this class of routines will be straightforward, and will provide efficient functions for calculating very large sets of data: different mean values, arbitrary moments, variance, standard deviation, covariance, skewness, kurtosis, correlation coefficient, auto-correlation, different random number and statistical distribution generators, data filtering, etc. All these functions will be registered with the Tcl interpreter of MMTools and will be available as simple commands in any Tcl script.

(d) Utility routines - will be used for different numerical calculations and will be based on popular freeware libraries for scientific computing such as Numerical Recipes [55] and the SLATEC library [56]. Similarly to the statistical routines, the implementation of these utility programs will be straightforward, and they will also be accessible to the researcher as simple Tcl commands. Initially, this class will contain functions and subroutines for the following: numerical integration and derivation, direct and inverse FFT, ODE and PDE solvers, Kramers-Kronig transformer, linear and non-linear curve fitting, linear and non-linear equation solvers. This class of routines will be extended on a continuous basis by adding new functions required by any of the MMTools or by any other program in the Routine Library.

4.3 MMTools Tutorial

The Tutorial for MMTools will have two main components, which will be distributed via the popular website of the Resource.

The first component of the Tutorial will consist of a Textbook, available in several different electronic forms, e.g., HTML, PDF, and PostScript. Both HTML and PDF versions will have hyperlinks for easy navigation through the text and the examples. The Textbook will have two parts. The first part will contain a systematic introduction to stochastic processes with examples from biophysics. The material presented there will be based on the lecture notes in non-equilibrium statistical mechanics mentioned in Sec. II. The second part of the book will contain a thorough description of MMTools. Each tool will be allocated a separate chapter, which will be divided into three parts. Part one will describe the rational and need for the tool, as well as the physical principles, including the relevant stochastic methods, on which the analysis tool is based. Part two will describe the structure, design and implementation of the tool. The role and functions of the individual procedures which build up the tool will be explained. Finally, part three will provide an example that illustrates how the tool is to be used.

An appendix will contain technical material such as a description of all functions and subroutines in the Routine Library, which represent the building blocks of the more complex procedures in MMTools: a brief introduction to the Tcl language; a detailed description on how to invoke MMTools as Tcl commands; and a presentation of the Tcl interface between MMTools, NAMD2 and VMD.

The second component of the Tutorial will consist of an ``Examples'' book, containing additional examples, exercises and suggested projects, inspired by completed and ongoing research projects conducted by Resource researchers. Each example will contain in electronic form the actual scripts used to apply MMTools in controlling the simulation, in collecting the relevant data and performing the desired analysis. The interested user will be able to reproduce all the results presented in the ``Examples'' book.

4.4 Dissemination and Training

Dissemination and training efforts will be accomplished mainly through electronic media. The Resource web site will continue to be a key dissemination and training vehicle. MMTools web pages containing full source code of freely distributed MMTools, searchable documentation, on-line tutorials and presentations will be constructed and maintained by the Resource. Leading federal and academic structural biology web sites with links to MMTools will establish visibility of the new suite of MD analysis tools in the biomedical community.

References

[1]: J. Koepke, X. Hu, C. Münke, K. Schulten, and H. Michel, The crystal structure of the light harvesting complex II (B800-850) from Rhodospirillum molischianum, Structure, 4:581-597, 1996.
[2]: P. E. Marszalek, H. Lu, H. Li, M. Carrion-Vazquez, A. F. Oberhauser, K. Schulten, and J. M. Fernandez, Mechanical unfolding intermediates in titin modules, Nature, 402:100-103, 1999.
[3]: J. Gullingsrud, R. Braun, and K. Schulten, Reconstructing potentials of mean force through time series analysis of steered molecular dynamics simulations, J. Comp. Phys., 151:190-211, 1999.
[4]: W. Nadler, A. Brünger, K. Schulten, and M. Karplus, Molecular and stochastic dynamics of proteins, Proc. Natl. Acad. Sci. USA, 84:7933-7937, 1987.
[5]: M. Nonella and K. Schulten, Molecular dynamics simulation of electron transfer in proteins: Theory and application to Q_A ® Q_B transfer in the photosynthetic reaction center, J. Phys. Chem., 95:2059-2067, 1991.
[6]: K. Schulten and M. Tesch, Coupling of protein motion to electron transfer: Molecular dynamics and stochastic quantum mechanics study of photosynthetic reaction centers, Chem. Phys., 158:421-446, 1991.
[7]: D. Xu and K. Schulten, Coupling of protein motion to electron transfer in a photosynthetic reaction center: Investigating the low temperature behaviour in the framework of the spin-boson model, Chem. Phys., 182:91-117, 1994.
[8]: M. A. Balsera, W. Wriggers, Y. Oono, and K. Schulten, Principal component analysis and long time protein dynamics, J. Phys. Chem., 100(7):2567-2572, 1996.
[9]: J. Rubner and K. Schulten, Development of feature detectors by self-organization: A network model, Biol. Cybernetics, 62:193-199, 1990.
[10]: J. Rubner, K. Schulten, and P. Tavan, A self-organizing network for complete feature extraction, In R. Eckmiller, G. Hartmann, and G. Hauske, editors, Parallel Processing in Neural Systems and Computers, pages 365-368. Elsevier, Amsterdam, 1990.
[11]: D. Xu, J. C. Phillips, and K. Schulten, Protein response to external electric fields: Relaxation, hysteresis and echo, J. Phys. Chem., 100:12108-12121, 1996.
[12]: J. Phillips and K. Schulten, Diffusive hysteresis at high and low driving frequencies, Phys. Rev. E, 52(3):2473-2477, 1995.
[13]: D. Xu and K. Schulten, Velocity reassignment echoes in proteins, J. Chem. Phys., 103:3124-3139, 1995.
[14]: D. Xu, K. Schulten, O. M. Becker, and M. Karplus, Temperature quench echoes in proteins, J. Chem. Phys., 103:3112-3123, 1995.
[15]: K. Schulten, H. Lu, and L. Bai, Probing protein motion through temperature echoes, In H. Flyvbjerg, J. Hertz, M. H. Jensen, O. G. Mouritsen, and K. Sneppen, editors, Physics of Biological Systems: From Molecules to Species, Lecture Notes in Physics, pages 117-152. Springer, 1997.
[16]: S. Izrailev, S. Stepaniants, M. Balsera, Y. Oono, and K. Schulten, Molecular dynamics study of unbinding of the avidin-biotin complex, Biophys. J., 72:1568-1581, 1997.
[17]: B. Isralewitz, S. Izrailev, and K. Schulten, Binding pathway of retinal to bacterio-opsin: A prediction by molecular dynamics simulations, Biophys. J., 73:2972-2979, 1997.
[18]: S. Stepaniants, S. Izrailev, and K. Schulten, Extraction of lipids from phospholipid membranes by steered molecular dynamics, J. Mol. Model., 3:473-475, 1997.
[19]: S. Izrailev, S. Stepaniants, B. Isralewitz, D. Kosztin, H. Lu, F. Molnar, W. Wriggers, and K. Schulten, Steered molecular dynamics, In P. Deuflhard, J. Hermans, B. Leimkuhler, A. E. Mark, S. Reich, and R. D. Skeel, editors, Computational Molecular Dynamics: Challenges, Methods, Ideas, volume 4 of Lecture Notes in Computational Science and Engineering, pages 39-65. Springer-Verlag, Berlin, 1998.
[20]: H. Lu, B. Isralewitz, A. Krammer, V. Vogel, and K. Schulten, Unfolding of titin immunoglobulin domains by steered molecular dynamics simulation, Biophys. J., 75:662-671, 1998.
[21]: D. Kosztin, S. Izrailev, and K. Schulten, Unbinding of retinoic acid from its receptor studied by steered molecular dynamics, Biophys. J., 76:188-197, 1999.
[22]: W. Wriggers and K. Schulten, Investigating a back door mechanism of actin phosphate release by steered molecular dynamics, PROTEINS: Struc., Func., and Genetics, 35:262-273, 1999.
[23]: A. Krammer, H. Lu, B. Isralewitz, K. Schulten, and V. Vogel, Forced unfolding of the fibronectin type III module reveals a tensile molecular recognition switch, Proc. Natl. Acad. Sci. USA, 96:1351-1356, 1999.
[24]: H. Lu and K. Schulten, Steered molecular dynamics simulations of force-induced protein domain unfolding, PROTEINS: Struc., Func., and Genetics, 35:453-463, 1999.
[25]: S. Izrailev, A. R. Crofts, E. A. Berry, and K. Schulten, Steered molecular dynamics simulation of the Rieske subunit motion in the cytochrome bc₁ complex, Biophys. J., 77:1753-1768, 1999.
[26]: M. Balsera, S. Stepaniants, S. Izrailev, Y. Oono, and K. Schulten, Reconstructing potential energy functions from simulated force-induced unbinding processes, Biophys. J., 73:1281-1287, 1997.
[27]: H. Lu and K. Schulten, Steered molecular dynamics simulation of conformational changes of immunoglobulin domain I27 interpret atomic force microscopy observations, Chem. Phys., 247:141-153, 1999.
[28]: D. Xu and K. Schulten, Multi-mode coupling of protein motion to electron transfer in the photosynthetic reaction center: Spin-boson theory based on a classical molecular dynamics simulation, In J. Breton and A. Vermeglio, editors, The Photosynthetic Bacterial Reaction Center: II. Structure, Spectroscopy and Dynamics, NATO ASI Series A: Life Sciences, pages 301-312. Plenum Press, New York, 1992.
[29]: K. Schulten, Curve crossing in a protein: Coupling of the elementary quantum process to motions of the protein, In D. Bicout and M. J. Field, editors, Proceedings of the Ecole de Physique des Houches, pages 85-118, Paris, 1995. Les Editions de Physique, Springer.
[30]: J. Ray and N. Makri, Short-range coherence in the energy transfer of photosynthetic light-harvesting systems, J. Phys. Chem. A, 103(47):9417-9422, 1999.
[31]: T. M. Martinetz, S. G. Berkovich, and K. Schulten, ``Neural gas'' for vector quantization and its application to time-series prediction, IEEE Trans. on Neural Networks, 4(4):558-569, 1993.
[32]: T. Martinetz and K. Schulten, Topology representing networks, Neural Networks, 7(3):507-522, 1994.
[33]: W. Wriggers, R. A. Milligan, K. Schulten, and J. A. McCammon, Self-organizing neural networks bridge the biomolecular resolution gap, J. Mol. Biol., 284:1247-1254, 1998.
[34]: H. Heller, M. Schaefer, and K. Schulten, Molecular dynamics simulation of a bilayer of 200 lipids in the gel and in the liquid crystal-phases, J. Phys. Chem., 97:8343-8360, 1993.
[35]: K. Schulten, W. Humphrey, I. Logunov, M. Sheves, and D. Xu, Molecular dynamics studies of bacteriorhodopsin's photocycles, Israel Journal of Chemistry, 35:447-464, 1995.
[36]: D. Kosztin, T. C. Bishop, and K. Schulten, Binding of the estrogen receptor to DNA: The role of waters, Biophys. J., 73:557-570, 1997.
[37]: J. C. Phillips, W. Wriggers, Z. Li, A. Jonas, and K. Schulten, Predicting the structure of apolipoprotein A-I in reconstituted high density lipoprotein disks, Biophys. J., 73:2337-2346, 1997.
[38]: L. Kalé, R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten, NAMD2: Greater scalability for parallel molecular dynamics, J. Comp. Phys., 151:283-312, 1999.
[39]: W. F. Humphrey, A. Dalke, and K. Schulten, VMD - Visual Molecular Dynamics, J. Mol. Graphics, 14:33-38, 1996.
[40]: M. Bhandarkar, G. Budescu, W. F. Humphrey, J. A. Izaguirre, S. Izrailev, L. V. Kalé, D. Kosztin, F. Molnar, J. C. Phillips, and K. Schulten, BioCoRE: A collaboratory for structural biology, In A. G. Bruzzone, A. Uchrmacher, and E. H. Page, editors, Proceedings of the SCS International Conference on Web-Based Modeling and Simulation, pages 242-251, San Francisco, California, 1999.
[41]: H. Heller, H. Grubmüller, and K. Schulten, Molecular dynamics simulation on a parallel computer, Molecular Simulation, 5:133-165, 1990.
[42]: A. Windemuth and K. Schulten, Molecular dynamics simulation on the Connection Machine, Molecular Simulation, 5:353-361, 1991.
[43]: H. Grubmüller, H. Heller, A. Windemuth, and K. Schulten, Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions, Molecular Simulation, 6:121-142, 1991.
[44]: J. A. Board, Jr., J. W. Causey, J. F. Leathrum, Jr., A. Windemuth, and K. Schulten, Accelerated molecular dynamics simulation with the parallel fast multipole algorithm, Chem. Phys. Lett., 198:89-94, 1992.
[45]: M. Nelson, W. Humphrey, A. Gursoy, A. Dalke, L. Kalé, R. Skeel, K. Schulten, and R. Kufrin, MDScope - A visual computing environment for structural biology, Comput. Phys. Commun., 91(1, 2 and 3):111-134, 1995.
[46]: W. Rankin and J. Board, A portable distributed implementation of the parallel multipole tree algorithm, IEEE Symposium on High Performance Distributed Computing, 1995.
[47]: M. Tuckerman, B. J. Berne, and G. J. Martyna, Reversible multiple time scale molecular dynamics, J. Chem. Phys., 97(3):1990-2001, 1992.
[48]: J. Leech, J. Prins, and J. Hermans, SMD: Visual steering of molecular dynamics for protein design, IEEE Comp. Sci. & Eng., 3(4):38-45, 1996.
[49]: A. Szabo, K. Schulten, and Z. Schulten, First passage time approach to diffusion controlled reactions, J. Chem. Phys., 72:4350-4357, 1980.
[50]: K. Schulten, U. Dinur, and B. Honig, The spectra of carbonium ions, cyanine dyes, and protonated Schiff base polyenes, J. Chem. Phys., 73(8):3927-3935, 1980.
[51]: W. Nadler and K. Schulten, Generalized moment expansion for Brownian relaxation processes, J. Chem. Phys., 82:151-160, 1985.
[52]: K. Schulten, Ensemble averaged spin pair dynamics of doublet and triplet molecules, J. Chem. Phys., 80:3668-3679, 1984.
[53]: K. Schulten, The effect of intramolecular paramagnetic-diamagnetic exchange on the magnetic field effect of radical pair recombination, J. Chem. Phys., 82:1312-1316, 1985.
[54]: H. Ritter, T. Martinetz, and K. Schulten, Textbook: Neural Computation and Self-Organizing Maps: An Introduction, Addison-Wesley, New York, revised English edition, 1992.
[55]: W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes in C, Cambridge University Press, New York, 2 edition, 1992.
[56]: The SLATEC Common Mathematical Library ((Version 4.1, July 1993) is a comprehensive software library containing over 1400 general purpose mathematical and statistical routines written in Fortran 77. It is freely available on the Internet at the following URL: http:/netlib2.cs.utk.edu/slatec/index.html.
[57]: S. Wolfram, The Mathematica book, Wolfram Media, Champaign, IL, 4th ed. edition, 1999.