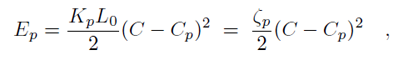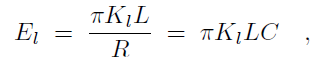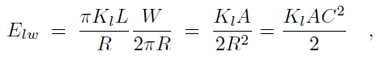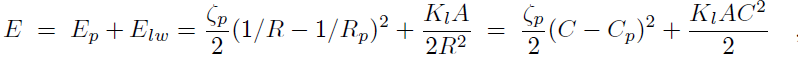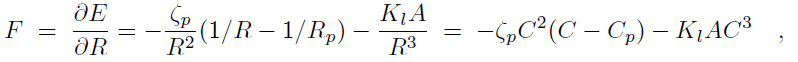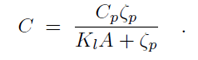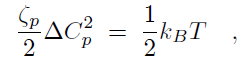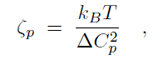Membrane Sculpting by F-BAR domains
Overview
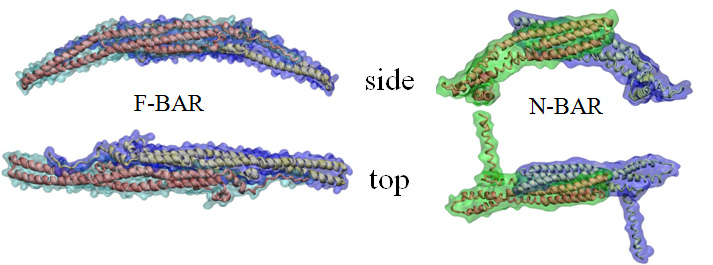
Interplay between cellular membranes and their peripheral proteins drives many cellular processes, including cell division, growth, movement and cell-cell communication. During their lifetime and often with the help of membrane peripheral proteins, eukaryotic cells dynamically sculpt their various types of compartments. Proteins of the Bin/Amphiphysin/Rvs (BAR) domain family play an important role in membrane remodeling, by inducing and stabilizing membrane curvature (see Figure 1 and Movie mpg movie 1, 4.0M, Movie mpg movie 2, 2.3M). Resolved structures show that BAR domains form crescent-shaped homodimers, the monomers being composed of coiled-coil association of a 3-helix bundle structure. Three sub-families of BAR domains, namely N-BAR domains, FCH-BAR (F-BAR) domains and Inverse-BAR (I-BAR) domains, differ from each other in their structure and physiological function. As previously reported, computational approaches revealed how membrane curvature is generated by N-BAR domains. In contrast to N-BAR domains that form a banana shaped dimer, F-BAR domains are elongated and only gently curved. A high density of positive charge is found on the part of the protein that is destined to interact with negatively-charged membranes. While N-BAR domains stabilize highly curved membrane structures, F-BAR domains stabilize membrane structures of small degree of curvature. N-BAR domains also have an N-terminal amphipathic helix, which aids membrane curvature stabilization by membrane insertion. Such helix is lacking in the case of F-BAR domains.
It remains unclear how membrane curvature depends on the type of F-BAR domain lattice arrangement. Two further open questions are: How do individual F-BAR domains interact with a membrane to form local curvature? What dynamics is involved in membrane curvature formation by F-BAR domain lattices?
The F-BAR domain binds and curves a membrane via scaffolding
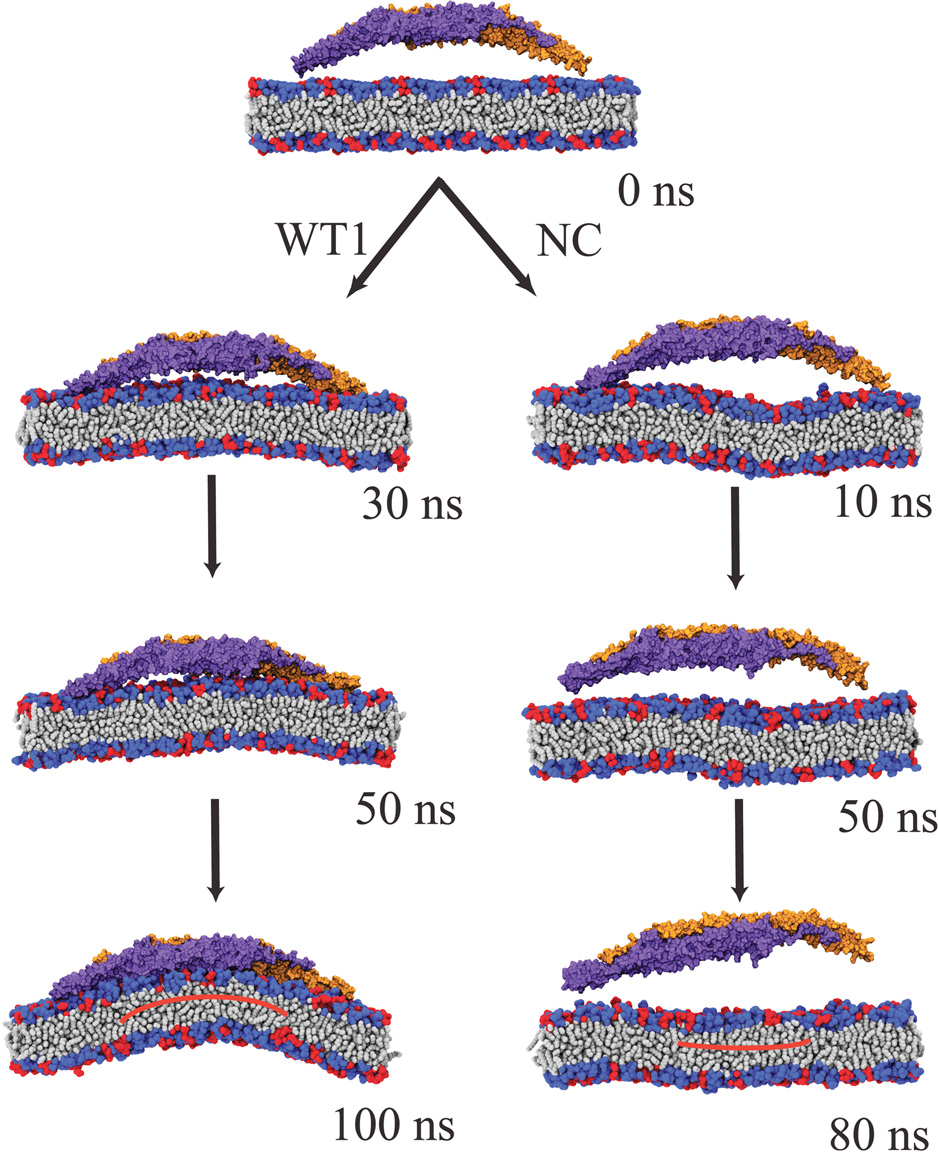
Two separate all-atom equilibrium simulations of single F-BAR domains shows contrasting results (see Figure 2). In simulation WT1, the wild type F-BAR domain was employed. Positive membrane curvature developed in 100 ns. In simulation NC, the positive charges of selected residues along the inner surface of the wild type F-BAR domain were neutralized without changing residue structure. F-BAR domain diffused away from the membrane within 80 ns.
In simulation WT1, the wild type F-BAR domain binds to the membrane within 30 ns, at which moment most positively charged residues are in close contact with the negative charges on DOPS headgroups; at this point the membrane curvature gradually increases to reach a maximum within 100 ns. Several positively charged residues are found to form close contacts with negatively charged DOPS headgroups. Two clusters of positively charged residues, cluster 1 (residues Lys27, Lys30, Lys33, Lys110, Arg113, Lys114, Arg121, Arg122) located at the center of the F-BAR domain and represented by Lys114 and Lys33, and cluster 2 (residues Lys132, Arg139, Lys140, Arg146, Lys150) represented by Lys132 and located at the side helices of the F-BAR domain, are found to form extensive contacts with DOPS headgroups in the course of the simulation. Indeed, clusters 1 and 2 are important for binding and membrane curvature formation; mutation of the residues mentioned can abolish lattice formation (Frost et al., Cell, 132:807 (2008)); most of the stated residues are conserved in both their sequence and structural context across different species and different F-BAR domains.
Theoretical description of the membrane sculpting process
Binding of the F-BAR domain to the membrane leads to a match between shapes of F-BAR domain and membrane. The resulting membrane curvature depends on the balance of two forces, one resisting protein shape changes and the other resisting membrane curvature changes. The bending energy of an F-BAR domain dimer attached to the membrane surface (or any other attached rod-like protein) can be described through
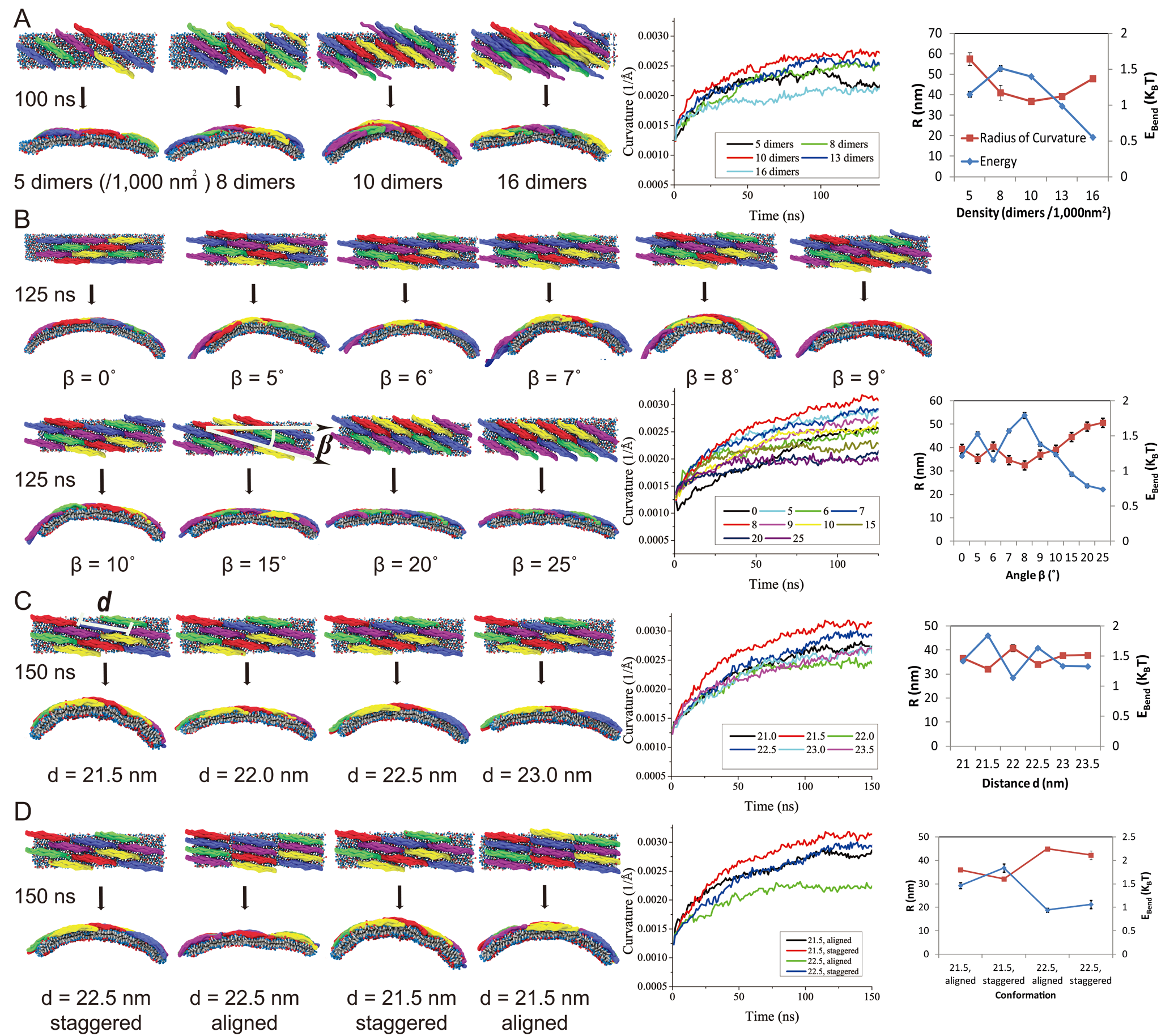
where Cp is the intrinsic curvature of the protein, C the curvature of the membrane, Kp the flexural rigidity of the protein, L0 the length of the protein, and ζp the protein bending rigidity. The curvature-related elastic energy of a cylindrical membrane of length L and radius R can be described by a Helfrich Hamiltonian where Kl is the membrane bending modulus. The curvature-elastic energy of a membrane patch of length L, width W and radius R can be described analogously by a Helfrich Hamiltonian, namely by where A is the area of the membrane patch (A = WL). The total energy of an F-BAR dimer binding to a membrane is then which corresponds to the shape force, F, At equilibrium holds F = 0 and, hence, According to the equipartition theorem of thermodynamics holds or where ΔCp is the curvature fluctuation of the protein, kB the Boltzmann constant and T the temperature.The intrinsic curvature of the protein was determined as the mean curvature of the protein, namely Cp = 0.0283 nm-1, corresponding to a radius of curvature of 35.3 nm. The root-mean square fluctuation of the curvature of the protein was determined from its standard deviation from the average protein curvature and was found to be ΔCp = 0.0062 nm-1. The membrane bending modulus Kl had been measured, through experiments and simulations, to be 20 kBT. The radius of curvature of an F-BAR dimer on top of a lipid patch is then estimated to be 45.1 nm. This value compares well with the radius of curvature monitored during the last 100 ns of simulation WT1, which is 48.1 nm.
With the parameters stated above, one can estimate the total binding energy of WT1 F-BAR dimer and membrane patch at equilibrium to be 2.30 kBT, with the bending energy of F-BAR dimer and of membrane patch contributing 0.74 kBT and 1.56 kBT, respectively. The average membrane curvature during the early (i.e., phase 1) period 38-40 ns is 0.12 nm-1 and amounts to the highest membrane curvature during the binding phase. During this period the total energy of the F-BAR-membrane system, the bending energy of the F-BAR dimer and of the membrane patch are 3.99 kBT, 3.47 kBT and 0.52 kBT, respectively. During the later (i.e., phase 2) period 78-80 ns the average membrane curvature is 0.20 nm-1 and amounts to the highest membrane curvature during the membrane bending phase. During this period the total energy of the F-BAR-membrane system, the bending energy of the F-BAR dimer and of the membrane patch are 2.34 kBT, 0.90 kBT and 1.44 kBT, respectively. Therefore, the total energy that is stored in the protein conformational change during membrane binding and membrane bending phases is (3.47 - 0.90) kBT = 2.57 kBT.
Binding and close adhesion of the F-BAR domain to the membrane require shape complementarity between protein and membrane. In case that both protein and membrane shapes are radially symmetric, i.e., the centerline of either one obeys in the x, z-plane the equation x2 + z2 = R2, shape complementarity leads to membrane curvature 1/R. If the F-BAR domains are forming on top of the initially planar membrane a lattice oriented (with the protein major axes) along the x-axis then the planar membrane coils into a tube with its long axes pointing along the y-axis.
However, in case that the F-BAR domain does not assume a radial shape, shape complementarity results in an interesting variation. To demonstrate this we assume that the F-BAR domain prefers either intrinsically or through the effect of adhesion to the membrane an ellipsoidal shape governed by the equation (x/a)2 + (y/b)2 = 1 where a and b are the major and minor axis of the ellipse. In this case a membrane tube along the y-axis does not permit close adhesion as the radially symmetric membrane and the ellipsoidal F-BAR domain don't match exactly. However, a tube tilted by an angle β relative to the y-axis permits a perfect match of protein and membrane shape. To see this we note that, according to a well known result of geometry, the tilted tube is cut by the x, z-plane along an ellipsoid. One can convince oneself readily that this ellipse has a short axis b = R and a long axis a = R/cosβ. One can then conclude that for the assumed ellipsoidally shaped F-BAR domains (characterized by long axis a and short axis b), forming a lattice oriented along the x-axis on an initially planar membrane, a tube of curvature 1/R results with direction along an angle β relative to the y-axis, where β is given by
This description assumes binding of the F-BAR domain leading to strong adhesion such that protein and membrane shape match very closely. In any case, a circular membrane tube can accommodate non-circular F-BAR domain shapes by rotating the tube axis, but only shapes that are nearly ellipsoidal. As stated already, such shapes can result from a combination of an intrinsic and an induced shape of the F-BAR domain dimer adhesion surface.Membrane curvature generated by F-BAR domain lattices
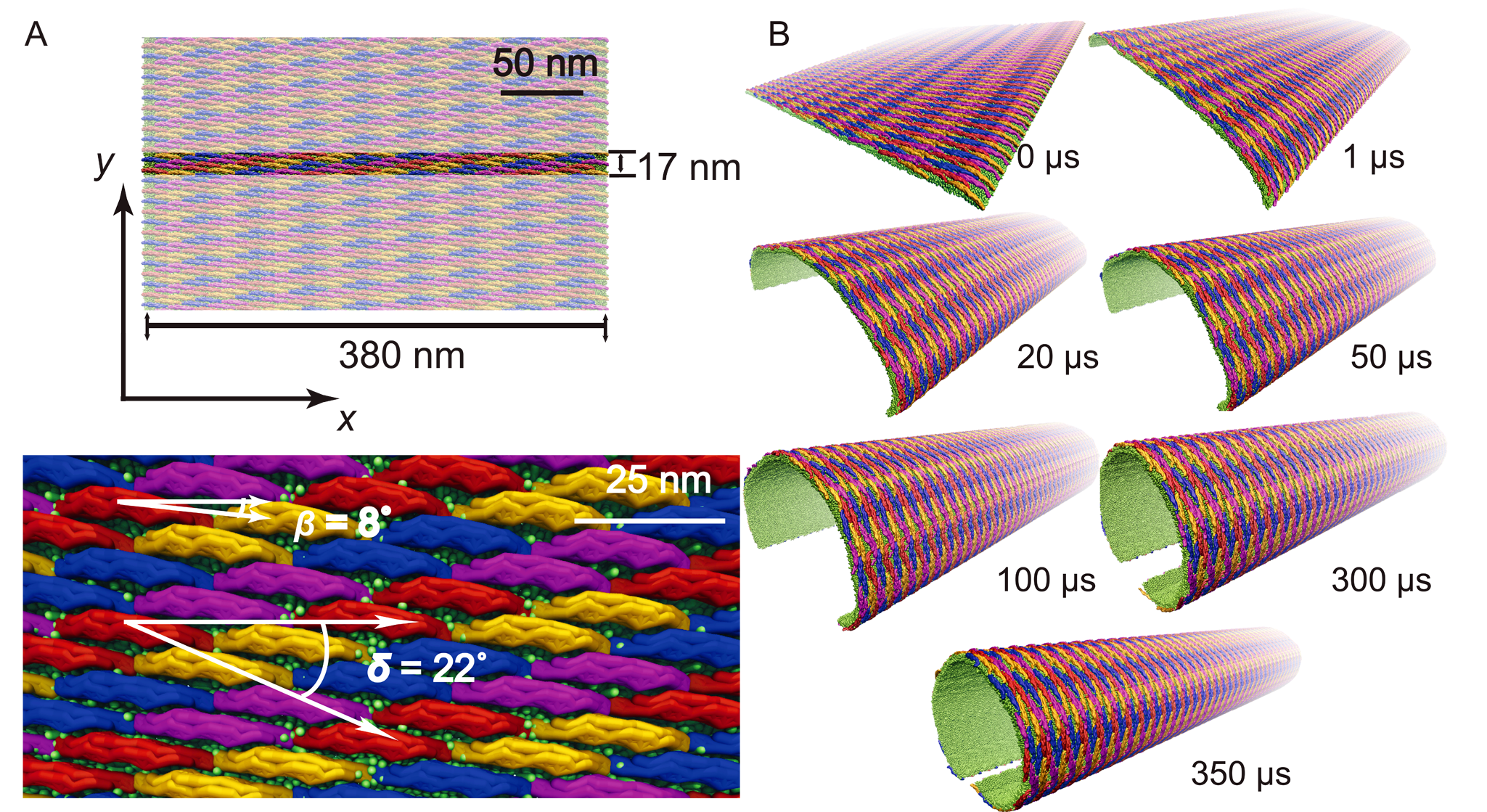
In a series of SBCG simulations, we examined how the F-BAR domain density affects membrane curvature. As Figure 4 shows, of the F-BAR domain lattices with five different densities, the one with 10 dimers per 1000 nm2 achieves highest curvature; lattices with lower densities achieve much lower curvature. This result is expected since the denser the lattices are, the more the F-BAR domains can act on the same area of lipid. However, membrane curvature becomes also reduced when the F-BAR domain density gets too high, due to neighboring F-BAR domains hindering each others' access to the membrane. This hinderance of neighboring domains increases as domain density increases. The F-BAR domain density generating the narrowest tubules, as seen in cryo-EM (Frost et al., Cell, 132:807 (2008)), is 8 to 10 dimers per 1000 nm2.
Figure 3 shows the relationship between membrane curvature and lattice geometry. Rather diverse curvatures (radii of curvature range from 25 to 100 nm) are seen to be generated by lattices with different parameters. High curvatures are generated by lattices with β values in the range of 5o - 9o. An inter-domain distance of 21.5 nm with the F-BAR domains being staggered in an end-to-shoulder arrangement yields the highest curvature. The results are consistent with recent cryo-electron microscopy images of F-BAR domain lattices on membrane tubules (Frost et al., Cell, 132:807 (2008)).
The observed tilt angle β = 8o between y-axis and tube axis suggests that the actual shape of the F-BAR domain membrane adhesion surface is ellipsoidal with axes a = 1.01 R and b = R, i.e., the widening of the F-BAR domain shape is very small, but significant enough to induce an observable reorientation of the tube axis. To understand how a deviation from circular shape as reflected by a = 1.01 R can be significant one should note that the lattice of F-BAR domains averages over the shape effect of many proteins such that even minor effects add up to the tube axis tilt.
Membrane tubulation by F-BAR domain lattices
To investigate how a complete tubule is formed by a lattice of F-BAR domains, the best (highest curvature induced) performing lattice was placed on a 380 nm wide planar membrane (see Figure 4 and Movie mp4 movie 3, 9.0M). Periodic boundary conditions in the y-direction imply that the lattice acts on an infinitely long membrane patch. Membrane curvature in simulation developed within hundreds of microseconds from the edges (curving first) to the center (curving last). After 350 μs, a tubular structure with local radius of curvature R = 60-90 nm was formed, with the edges being separated by only 28 nm. In lieu of using more computer time (the simulation stretched over 10 months), we applied a weak radial force until the edges met, fusing the membrane into a complete tubular structure. After the tube was closed, we removed all F-BAR domains and carried out 30 μs of further equilibrium simulation, during which the tube remained closed. Tubules formed by the F-BAR domain lattices in vivo range from 25 to 100 nm in radius. In a second simulation we observed a tube fusing event in which one edge of a tube met the other edge in a T-like junction. Removing all F-BAR domains and continuing the simulation for 30 μs revealed again a stable structure.
Structures
Equilibrated F-BAR domain pdb structure from WT1 simulation at 200 ns FBAR.pdb, 723K
Please cite this website and the following publication when using this structure.
Membrane Sculpting by F-BAR domains, http://www.ks.uiuc.edu/Research/FBAR.
Publications
Investigators
Related TCB Group Projects
- Membrane Sculpting by BAR domains
- Intrinsic Curvature Properties of Photosynthetic Proteins in Chromatophores
- Coarse-Grained Molecular Dynamics
Page created and maintained by Hang Yu.