Most classical molecular dynamics (MD) simulations employ potential functions that do not account for the effects of induced electronic polarization between atoms, instead treating atoms as simple fixed point charges. Incorporating the influence of polarization in large-scale simulations is a critical challenge in the progress toward computations of increased fidelity, providing a more realistic and accurate representation of microscopic and thermodynamic properties.

The Drude oscillator model represents induced electronic polarization by introducing an auxiliary particle attached to each polarizable atom via a harmonic spring. The advantage with the Drude model is that it preserves the simple particle-particle Coulomb electrostatic interaction employed in nonpolarizable force fields, thus its implementation in NAMD is more straightforward than alternative models for polarization. Performance results below show that the implementation of the Drude model maintains good parallel scalability, with an increase in computational cost by not more than twice that of using a nonpolarizable force field.

The linked movie animates frames from a Drude water simulation. The Drude particles are shown as the smaller green spheres springing out from the oxygen atoms shown in red.

Background

To model the polarizability $\alpha$ of a given atom with partial charge $q$, a mobile Drude particle carrying a charge $q_\D$ is introduced. The charge of the atom is replaced by $q-q_\D$ to preserve the net charge of the atom-Drude pair. The Drude particle is harmonically bound to the atomic particle with a large force constant $k_\D$. In the absence of a field, the Drude particle oscillates around the position of the atom $\vec{r}$, and the atom appears on average as a point-charge $q$ at $\vec{r}$. In the presence of an electric field $\vec{E}$, the Drude particle oscillates around a displaced position $\vec{d} = q_\D \vec{E}/k_\D$, and the average induced atomic dipole is $\vec{\mu} = q_\D^2 \vec{E}/k_\D$. It follows that the isotropic atomic polarizability of the atom can be expressed as $\alpha=q_\D^2/k_\D$.

Extending a molecular system by adding auxiliary Drude particles yields the polarizable force field, $U = U_{\text{self}} + U_{\text{bond}} + U_{\text{elec}} + U_{\text{LJ}}$, where $U_{\text{self}}$ represents the atom-Drude harmonic bonds, $U_{\text{bond}}$ is the contribution from the bonded internal energy terms (bonds, angles, and dihedrals), $U_{\text{elec}}$ represents all Coulombic electrostatic interactions (atom-atom, atom-Drude, and Drude-Drude), and $U_{\text{LJ}}$ is the Lennard-Jones "12-6" interaction. The electrostatic interactions for the 1-2 and 1-3 nuclei pairs with their associated Drude particles are treated with shielding functions designed by Thole [5, 6]. The force constant $k_D$, which is assumed to be the same for all atoms without any loss of generality in the value of $\alpha$, is chosen such that the displacement $\vec{d}$ of the Drude particle remains much smaller than any interatomic distance, such that the resulting induced dipole $\vec{\mu}$ is almost equal to a point-dipole.

The self-consistent field (SCF) regime of induced polarization is obtained by allowing the Drude particles to relax to their local energy minima for any given fixed configuration of nuclei in the system. However, this procedure is computationally prohibitive. It is much more efficient to instead approximate the SCF energy surface using an extended Lagrangian dynamics strategy in which the Drude particles are allowed to carry kinetic energy. The Drude oscillators are maintained with a thermostat at a low temperature $T^{\star}$, chosen sufficiently small to leave only a small amount of kinetic energy in the atom-Drude oscillators, yet sufficiently large to allow the oscillators to continuously readjust their configurations to the room-temperature motion of the nuclei.

Integration

The integration of the extended Lagrangian is performed using a dual thermostat to keep the Drude oscillators at a cold temperature $T^{\star}$ while the remaining warm degrees of freedom are maintained at a desired temperature $T$. In a previous implementation of the Drude model, this was achieved by designing a dual Nosé-Hoover thermostat acting on, and within, each nucleus-Drude pair [3]. In the present implementation for NAMD, this is achieved via dual stochastic Langevin thermostats. A Langevin thermostatting scheme is advantageous for high performance computing platforms because it can be implemented locally, while avoiding the global communication of the kinetic temperatures $T$ and $T^{\star}$ required by the Nosé-Hoover scheme. Furthermore, a Langevin thermostatting scheme is extremely effective at equipartitioning energy, which confers a great dynamical stability in large-scale heterogeneous biomolecular systems.

The desired integration is obtained by separating the dynamics of each atom-Drude pair with coordinates $\vec{r}_i$ and $\vec{r}_{\D,i}$ in terms of the global motion of the center-of-mass $\vec{R}_i$ and the relative internal motion of the oscillator $\vec{d}_i = \vec{r}_{\D,i} - \vec{r}_i$. Denoting $m_i$ as the total mass of the pair and $m_i' = m_\D (1 - m_\D / m_i)$ as the reduced mass of the oscillator, the equations of motion of the Drude-atom pair are \begin{equation} m_i \frac{\d^2}{\d t^2} \vec{R}_i = \vec{F}_{\vec{R},i} - \gamma \frac{\d}{\d t} \vec{R}_i + \vec{f}_i, \tag{1} \end{equation} \begin{equation} m_i' \frac{\d^2}{\d t^2} \vec{d}_i = \vec{F}_{\vec{d},i} - \gamma\,' \frac{\d}{\d t} \vec{d}_i + \vec{f}_i', \tag{2} \end{equation} where $\vec{F}_{\vec{R},i} = -\partial\, U / \partial\, \vec{R}_i$ and $\vec{F}_{\vec{d},i} = -\partial\, U / \partial\, \vec{d}_i$ are the forces acting on the center-of-mass and on the reduced mass, respectively. The coupling to dual heat baths is modeled by the addition of damping and noise terms, where $\gamma$ and $\gamma\,'$ are external and internal Langevin friction coefficients. The $\vec{f}_i$ and $\vec{f}_i'$ are time-dependent fluctuating random forces obeying the fluctuation-dissipation theorem, $\vec{f}_i = (2\gamma\, k_{\text{B}} T/m_i)^{1/2} R(t)$ and $\vec{f}_i' = (2\gamma\,' k_{\text{B}} T^{\star}/m_i')^{1/2} R'(t)$, where $R(t)$ and $R'(t)$ are univariate Gaussian random processes. The temperature $T$ of the "physical" thermostat is chosen to keep the atoms while the temperature $T^{\star}$ is set to a small value in order to reduce the thermal fluctuation of the Drude oscillators. If $T^{\star}$ is set to 0, the thermostat on the oscillators is eliminated. For low values of $T^{\star}$, the actual Drude oscillator temperature maintained by the thermostat will depend mostly on the balance between energy dissipated by the damping term and energy introduced by electrostatic coupling to the environment. The forces on the centers-of-mass and on the displacements can be expressed in terms of the actual forces on the particles \begin{equation} \vec{F}_{\vec{R},i} = -\frac{\partial\, U}{\partial\, \vec{r}_i} - \frac{\partial\, U}{\partial\, \vec{r}_{\D,i}}, \tag{3} \end{equation} \begin{equation} \vec{F}_{\vec{d},i} = -\Bigl( 1 - \frac{m_\D}{m_i} \Bigr) \frac{\partial\, U}{\partial\, \vec{r}_{\D,i}} + \Bigl( \frac{m_\D}{m_i} \Bigr) \frac{\partial\, U}{\partial\, \vec{r}_i}. \tag{4} \end{equation}

Extensions to the force field

The Drude polarizable force field requires some extensions to the CHARMM force field. The Drude oscillators differ from typical spring bonds only in that they have an equilibrium length of zero. The Drude oscillators are optionally supplemented by a maximal bond length parameter, beyond which a quartic restraining potential is also applied. The force field is also extended by an anisotropic spring term that accounts for out-of-plane forces from a polarized atom and its covalently bonded neighbor with two more covalently bonded neighbors (similar in structure to an "improper" bond). The screened Coulomb correction of Thole is calculated between atom-Drude pairs that are otherwise excluded from nonbonded interactions.

The new polarizable force field based on classical Drude oscillators also includes the use of off-centered massless interaction sites, i.e., "lone pairs" (LPs), to avoid the limitations of centrosymmetric-based Coulomb interactions [1]. Support for these massless sites requires some additional extension to NAMD. The coordinate of each LP site is constructed based on three "guide" atoms. The calculated forces on the massless LP must be transferred to the guide atoms, preserving total force and torque. After an integration step of velocities and positions, the position of the LP is updated based on the three guide atoms, along with additional geometry parameters that give displacement and in-plane and out-of-plane angles.

Implementation details

NAMD integrates the Langevin equation using the Brünger-Brooks-Karplus (BBK) method, a natural extension of the Verlet algorithm. Extension of the atom-based Langevin equation to accommodate the dual thermostats for Drude oscillators required only small modifications to the existing source code. Because the integration of the centers-of-mass and the displacements is identical to the integration of the individual atoms, except for the update of the velocities with the thermostats, NAMD treats the entire system in standard atomic coordinates until the application of the thermostats to velocities, at which point an atom-Drude oscillator pair is transformed to center-of-mass and relative displacement coordinates, the respective thermostats are applied to the transformed coordinates, and the coordinates are transformed back to standard atomic coordinates. Independent of the Drude particle attached to the oxygen, the model also imposes a rigid geometry to the Drude water model SWM4-NDP, which is implemented via the Settle algorithm.

The PSF file format is presently extended to include Drude particles and LPs listed with the atoms. The number of columns in the "atoms" section is increased to include the alpha and thole parameters needed for the screened Coulomb correction of Thole. The Drude particles are required to immediately follow their parent atoms and the LPs follow the hydrogens bonded to their parent atom. Two new sections are introduced: one giving the anisotropic spring interactions and associated force constants, and the other giving lone pair guide atoms and associated geometry parameters.

The Drude oscillators (the $U_{\text{self}}$ term) are evaluated as part of the NAMD ComputeBonds class that performs evaluation of the typical spring bonds. The anisotropic spring interactions are evaluated in the new compute class ComputeAniso with the energy added into the spring bond energy reduction. The screened Coulomb correction of Thole are evaluated in the new compute class ComputeThole with the energy added into the electrostatic energy reduction.

For scalable parallelism, NAMD performs a spatial decomposition of atoms into "patches" [4]. NAMD further partitions the atoms into "hydrogen groups" that keeps hydrogen atoms within the same spatial patch as its parent atom to which it is covalently bonded. This convention keeps each pair of atoms needed for imposing bond constraints together on the same processor. The LPs require a similar treatment. Since the force transfer and position updates must, respectively, follow and precede the force computation and communication phases, the cluster of atoms needed for an LP must be kept together on a processor for efficiency. To accomplish this, NAMD has been augmented to maintain "migration groups" as a superset of hydrogen groups, designed to keep the atoms in a group within the same patch, and thus on the same processor. Since migration groups are a little larger than hydrogen groups, the patch lengths must be padded at the edges with some extra space to ensure that migration groups separated by a patch do not come within the nonbonded cutoff distance of each other before the next atom migration, at which time an entire migration group might be moved to an adjacent patch. The set of guide atoms needed to determine the geometry of the LPs is set in the residue topology file (RTF). For maximum effectiveness, they are chosen to allow the splitting of large biomolecules (proteins, lipids, and nucleic acids) into the smallest possible independent migration groups. For example, in polypeptides and proteins this requires avoiding any overlap of guide atoms between successive residues. If patches become too large spatially (and too dense, due to the extra Drude particles and LPs), the existing NAMD two-away patch splitting can be used in any or all of the $x$-, $y$-, and $z$-dimensions.

Performance results

The use of Drude polarizable force field generally increases the computational density (and thus the cost) of simulating a system of atoms by about a factor of 5/3, due to the use of a water model having five charge sites (three atoms, one LP, and one Drude particle) rather than three. The additional work needed to calculate extra force terms and to redistribute the lone pair forces also scales linearly with the size of the system.

---

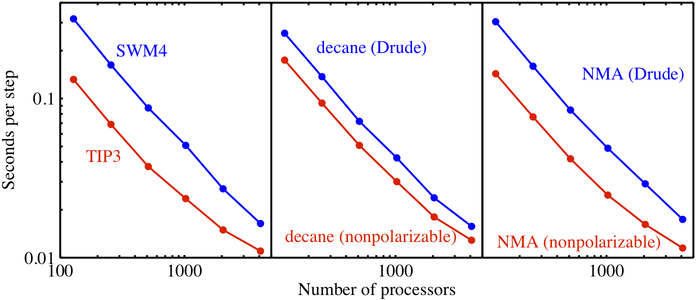
Figure 1: NAMD scalability, with Drude model in blue and nonpolarizable in red. Systems comprise 72 000 water molecules, 8576 decane molecules, and 18 944 N-methylacetamide (NMA) molecules.

---

Three basic systems that together include all features of the Drude model have been simulated: SWM4-NDP (water with four charge sites and negative Drude particle [2]), decane, and N-methylacetamide (NMA). Figure 1 shows the parallel performance of NAMD on Blue Gene/P for all three systems modeled with and without polarizability. The test systems were simulated under isothermal-isobaric (NPT) condition at 298.15 K. For each system, 20 000 steps of MD simulations were carried out for both the polarizable and nonpolarizable CHARMM force field. For all three systems, the Drude computations scale well to 4096 processors (1 standard Blue Gene/P rack). For the nonpolarizable model, linear scaling holds only up to 2048 processors due to the smaller number of particles that is known to limit linear scaling. The SWM4-NDP system exhibits the largest relative speed ratio between the Drude model and the nonpolarizable model, about 1:2. The relative speed ratio of decane is about 1:1.6, and NMA has a ratio of about 1:1.8. These ratios demonstrate that the present implementation of the Drude model in NAMD is quite efficient, requiring no more than twice the computational cost of the nonpolarizable model.

References

[1]

E. Harder, V. M. Anisimov, I. V. Vorobyov, P. E. M. Lopes, S. Y. Noskov, A. D. MacKerell, and B. Roux. Atomic level anisotropy in the electrostatic modeling of lone pairs for a polarizable force field based on the classical drude oscillator. Journal Of Chemical Theory And Computation, 2(6):1587–1597, 2006.

[2]

G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux, and A. D. MacKerell. A polarizable model of water for molecular dynamics simulations of biomolecules. Chemical Physics Letters, 418(1-3):245–249, 2006.

[3]

G. Lamoureux and B. Roux. Modeling induced polarization with classical Drude oscillators: Theory and molecular dynamics simulation algorithm. Journal Of Chemical Physics, 119(6):3025–3039, 2003.

[4]

JC Phillips, R Braun, W Wang, J Gumbart, E Tajkhorshid, E Villa, C Chipot, RD Skeel, L Kale, and K Schulten. Scalable molecular dynamics with NAMD. J Comput Chem, 26:1781–1802, 2005.

[5]

B. T. Thole. Molecular polarizabilities calculated with a modified dipole interaction. Chem. Phys., 59:341–350, 1981.

[6]

P.T. Van Duijnen and M. Swart. Molecular and atomic polarizabilities: Thole’s model revisited. J. Phys. Chem. A, 102(14):2399–2407, 1998.

Sample simulation files

The Drude model is still under development, and the NAMD setup tools have not yet been extended to generate the necessary PSF for Drude simulation. Files for small sample systems including Drude water (SWM4-NDP), decane, and NMA are available below for downloading.

• water (216 molecules)
• decane (1 molecule)
• NMA (1 molecule)

Publications

Investigators

• David Hardy
• Jim Phillips

Collaborators

• Benoit Roux (University of Chicago)
• Alexander D. MacKerell, Jr. (University of Maryland)
• Wei Jiang (Argonne National Laboratory)

Page created and maintained by David Hardy.