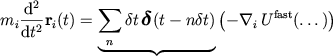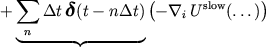Algorithms


Molecular Dynamics

Atomic positions obey Newton's second law

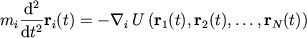
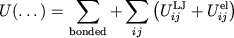
equation
where
equation
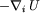The evaluation of the forces expression is very time consuming. To speed up these calculations, NAMD uses:
  1. parallelism,
  2. a fast multipole algorithm, and
  3. multiple time stepping (MTS).

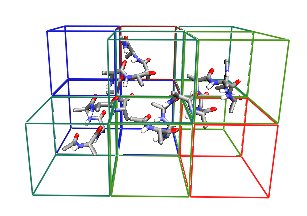
spatial decomposition
Spatial Decomposition

NAMD divides the simulation space into rectangular regions called patches. Each patch is responsible for updating the coordinates of the atoms contained in its region of space. Patch dimensions are chosen to be greater than the cutoff radius for non-bonded interactions, which eliminates the need for communication between non-adjacent patches. A cluster of adjacent patches is assigned to each processor. This design reduces the amount of interprocessor communication, enabling scalable parallelism.


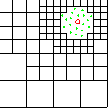
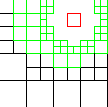
particles particles level 3 level 3
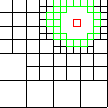
level 4 level 4 level 2 level 2

Enhanced Parallel Fast Multipole Algorithm
(Board et al. 1995)

The effect of a charged particle is represented directly at a short length scale. At longer length scales its effect is pooled with other charges and represented by a multipole expansion, which is transfered to distant cubes and expressed as Taylor expansions.



Verlet-I / r-RESPA / Impulse MTS Method

Forces are approximated by a sequence of impulses:

equation
small timestep
equation
large timestep

Partitioning the potential energy as

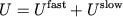
equation
allows the more numerous (long-range) slow interactions to be computed less frequently.

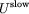expression consists of long-range electrostatics,

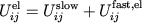
equation
slow part fast part
slow part fast part


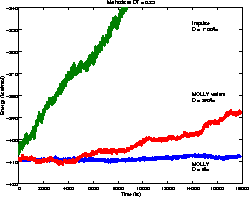
Mollified Impulse Method

The Impluse MTS method is unstable unless:

slow-force 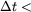equation half the period of the highest frequency fast-force motion

This is overcome by the Mollified Impulse method (MOLLY).

Define vibration-averaged positions

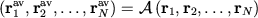
equation
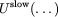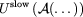and replace expression by expression in the Impulse MTS method.

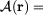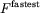
expression projection in configuration space of positions onto equilibrium manifold for expression

vibration-averaged positions

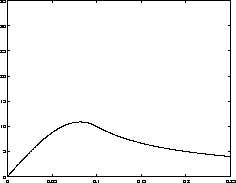
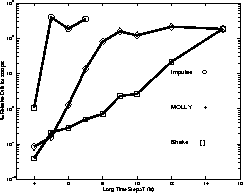
Some graphical MOLLY results:

total energy vs. time percent relative drift vs. time
total energy vs. time for equation 6.25 fs percent relative drift vs. time


Timesteps for Different Interactions

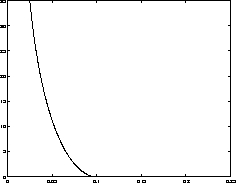
For a harmonic oscillator:

choosing 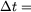equation 1/12
gives frequency error 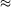equation 1.14%

The generalized period for an interaction is

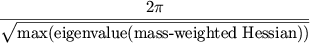
expression
where the Hessian of an interaction is the matrix of 2nd derivatives of its potential.

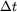Examples of expression:

Normal mode analysis of
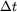
125 water molecules 		period(s) expression
bond length stretching 9.9, 10.1 fs 0.8 fs
bond angle bending 18.9 fs 1.6 fs

Simulations measuring
the generalized period
of the Lennard-Jones
potential for 125 water
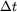
molecules at 300 K 		total time worst case expression
10 fs 2.3 fs
100 fs 2.0 fs
1000 fs 1.7 fs


Avoiding Distance Calculations

By construction

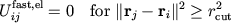
equation
This is true for most atom pairs.

To avoid most redundant distance calculations, monitor atom movement after patch assignment. Choose expression to be the maximum distance traveled by an atom.

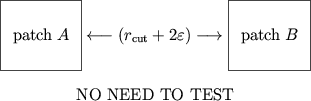
diagram


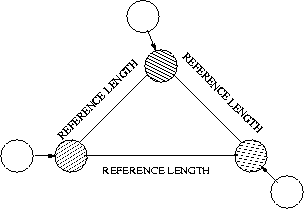
Multiple Grid N-body Solvers

These are interpolation-based solvers which utilize a splitting of the potential into short-range and smooth long-range parts:

  • short-range contribution: direct calculation using spatial hashing
  • long-range contribution: approximate fast matrix-vector product on a grid using a multilevel method

The motivation is to be faster than the fast multipole algorithm:

  • relative simplicity of the algorithm enables the avoidance of black box overhead
  • continuity of forces results in stable time stepping
  • continuity of force decomposition results in stable multiple time stepping

The following tables compare an initial implementation of the multiple grid N-body solver with DPMTA (Board et al.), a fast multipole implementation. The test system was a 60 Angstrom box of water containing a total of 20544 atoms. The timings were performed after compiling both codes with the cc -fast option on a Sun Ultra-60.

Multiple grid N-body solver (cutoff radius = 8 Angstroms)
grid spacing
(Angstroms) 		average force
error (%) 		maximum force
error (%) 		energy
error (%) 		time
(seconds)
4.36 0.29 1.32 0.0013 1.87
2.77 0.17 0.67 0.0024 2.95
2.03 0.14 0.58 0.0017 8.15

DPMTA, fast multipole implementation (theta = 0.75)
number
of terms 		average force
error (%) 		maximum force
error (%) 		energy
error (%) 		time
(seconds)
4 0.30 1.83 0.0004 6.49
8 0.02 0.25 0.0002 8.42


Fast Matrix-Vector Product on a Grid

The electrostatic potential energy due to N charged particles is

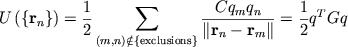
equation
where the set of exclusions includes all self-interactions and typically any pairs of atoms involved in some bonded interaction.

To compute the long-range contribution, we need to form the product 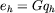equation which is obtained by approximating the smooth part of G on a grid of spacing h.

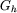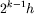A fast way to do this is to approximate the smooth part of expression on a coarser grid with spacing 2h. Using superscript k to represent a grid with spacing expression the computation through L grid levels is represented schematically:

computation schematic