Primary Absorption of a Photon
Purple bacteria have developed under relentless evolutionary pressure in a habitat below that of most plant life - that is, at the bottom of ponds or in topsoil, depending on the species. Only light left unharvested by plants penetrates to those depths, mainly at wavelengths at about 500 nm and above 800 nm.
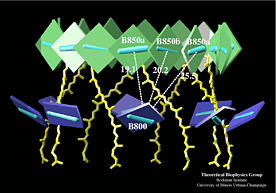
Carotenoids in light-harvesting complexes of purple bacteria absorb at 500 nm. Bacteriochlorophylls absorb at 800 - 875 nm. In LH-II, there exist two kinds of BChls,
Click on the figure for an 87 kB version of the chromophore arrangement
The figure was produced with our graphics program VMD .
B800 BChls and B850 BChls, absorbing at 800 and 850 nm, respectively. B800 and B850 BChls are oriented perpendicular to each other so that they can absorb light from every direction.
While the B800 BChls are spatially separated (center -to-center) by 20 Angstroms, B850 BChls form a ring of close (around 9 Angstroms) and, thus, tightly coupled BChls. To characterize the electronic properties of the excited states of a circular BChl aggregate, we have established an effective Hamiltonian description.
The excited states of the aggregate, so-called excitons , are described as a superposition of single BChl Qy excitations
[1],
[2] .
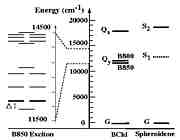
The energies associated with the eigenstates (exciton states) of the effective Hamiltonian for the B850 BChl aggregate of LH-II of Rs. molischianum are shown below together with the energies of the excited states of single BChls and the carotenoid spheroidene. The two bands in the spectrum arise from a dimerization of the BChls in LH-II and LH-I, i.e., the distance between neighboring BChls within one heterodimer (9.2 Angstrom in LH-II), is different from the distance between neighboring BChls between heterodimers (8.9 Angstrom in LH-II).
Optical Properties
Click on the figure for an 18 kB version of the spectrum
A key feature of the electronic excitations connected with the B850 BChl spectrum above is the distribution of oscillator strength of the exciton states, i.e., the ability of the states to absorb or emit light directly. Only the energetically degenerate pair of states |2>, |3> above the lowest energy state |1> carry non-zero oscillator strength. Due to a well-known sum rule, the addition of all oscillator strengths of the exciton band system, in the effective Hamiltonian description, must be equal to the sum of Qy state oscillator strength Dy of the individual BChls (equal 16Dy), i.e., |2> and |3> must each carry oscillator strength 8Dy. This so-called superradiance reflects the property of the exciton states |2>, |3> to be coherent superpositions of Qy excitations of individual BChls. Likewise the vanishing of oscillator strength of state |1> reflects a coherent spread of excitations around the entire BChl ring.
--> The ring structure increases absorption
The distribution of oscillator strength can have important functional implications: excitation of the B850 BChl system would result, after thermal relaxation, in the preferential population of the energetically lowest exciton state |1> which is optically forbidden due to its vanishing oscillator strength and, hence, is prevented from wasteful fluorescence. The population of state |1> would depend sensitively on the actual energy difference between |1> and the energetically degenerate states |2>, |3>.
--> The ring structure generates an energy trap
One must note that the properties of the B850 BChl system outlined hinge much on the ideal eight-fold symmetry axis of LH-II of Rs. molischianum. Distortions due to thermal motion or interruptions of the complete circle would alter the oscillator strength distribution. The characteristics of the exciton states due to a complete coherent spread of the excitations over the LH-II ring need to be studied in the presence of distortions. It is widely believed that the B850 BChl excited states, despite natural disorder, are delocalized, but the extent of delocalization is debated. The estimate for the number of coherently coupled BChls ranges from two BChl molecules to the entire length of the B850 BChl aggregate. The treatment of dynamic disorder for an exciton system like that of the Qy excitons in LH-II is technically extremely difficult and essentially impossible. One needs to describe respective systems mathematically in the product space of quantum states and of stochastic states. Descriptions achieved so far restrict the stochastic space to two states. Desirable would be a sampling of an effective state space of the B850 BChl ring in LH-II through a molecular dynamics simulation, abstraction of a stochastic operator which would account for the monitored transitions between stochastic states, and a subsequent stochastic quantum mechanical description. For two-state quantum systems such treatment has been achieved in [Ref] .
