PHI: Parallel Hierarchy Integrator
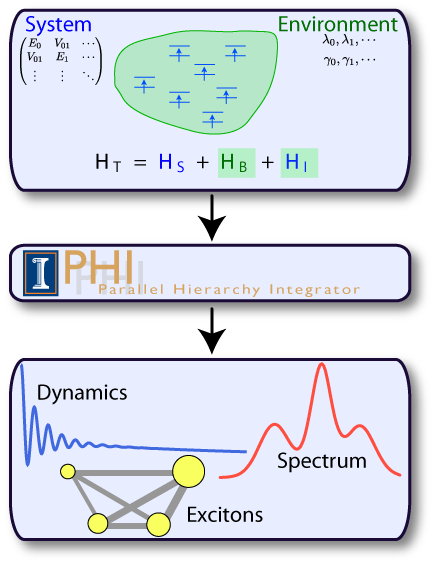Fig 1: PHI can be used to simulate a finite sized quantum system that is
embedded in a harmonic bath.Calculating Quantum Dynamics
Many systems require quantum mechanics for accurate representation. To theoretically investigate the dynamics of such systems is often extremely challenging from a modeling point of view and also from a computational point of view. This challenge is compounded by the influence of a thermal environment that can absorb and donate energy. Such systems often arise in biology and particularly in photosynthetic organisms.
The challenge in describing photosynthetic systems arises from two sources: (1) quantum coherence between excited pigment molecules; (2) non-Markovian dynamics arising from a strongly coupled thermal environment. Simultanously accounting for both sources has proven to be theoretical and computational challenge, prohibiting the calculation of many-pigment excited state dynamics that occur in a protein environment.
The theoretical challenge has been addresses by only a few different methods, of which one, the hierarchy equations of motion (HEOM) (Tanimura and Kubo, J. Phys. Soc. Jpn. 1989), has become the "gold standard" that others are compared against. This has been due to the method’s general applicability across many parameter ranges and in-spite of the computational expense associated with the HEOM.
The computational expense of the HEOM has been typically side-stepped by studying only small systems, comprising typically two states. The investigation of quantum dynamics in photosynthetic systems requires, however, that large, many-pigment systems be tractable. To achieve this tractability we have implemented the HEOM for multi-processor computers (Strumpfer and Schulten, J. Chem. Theor. Comp. 2012) in publicly available software PHI.
HEOM on Parallel Computers
The HEOM are a set of coupled differential equations that can easily number greater than 100,000 (depending on system parameters). With a parallel computer we can solve this many equations simultaneously by having each processor numerically integrate a subset of the equtions. The coupled nature of the equations requires however that the processors communicate their calculated integration updates at each timestep (or multiple times during a timestep for higher order integration schemes). The extreme communication cost of the numerical integration precludes the use of distributed memory parallel computers until inter-node network speeds are dramatically improved. As such, PHI currently utilizes shared memory parallel computers where the inter-processor communication bandwith is sufficient for reasonably sized photosynthetic systems.
Fig 2: PHI performance is due to an efficient hierarchy partitioning scheme that minimizes inter-processor communication.
PHI employs a unique partitioning scheme to split up integration work between different processors. The partitioning scheme exploits the communication structure of the HEOM. The HEOM can be visualized as a d-dimensional Pascal’s simplex for a system containing d states. Each vertex in the Pascal’s simplex corresponds to a d x d matrix that has an associate differential equation. Communication between vertices in a given level of the simplex only occurs with vertices in level directly above and directly below. PHI exploits this structure to minimize communication and thus dramatically improve numerical integration times (see Fig. 2).
Integration methods
For an additional performance boost PHI employs adaptive timestep integration: the Runga-Kutta-Fehlberg 4/5 (RKF45) method. The HEOM furnish the noise-averaged density matrix time evolution and, thus, exponentially approaches a steady-state. Fluctuations from the initial state are thus damped out over time. By employing adaptive integration short timesteps can be used to account for the early time evolution of the density matrix, and long timesteps for the later time evolution of the density matrix.Uses
The numerical performance of PHI allows that the dynamics of systems up to 50 states can be calculated even with strong inter-state coupling values and high reorganization energies. As such, PHI can be used in the context of photosynthesis to calculate excited state dynamics of multi-complex systems as they are found in photosynthetic organisms. In the case of purple bacteria PHI has been employed to examine excitation transfer from LH2 to LH2, from LH2 to LH1 and from LH1 to RC.Publications
Investigators
Related TCB Group Projects
Page created and maintained by Johan Strumpfer.
