FMO Excitation Dynamics
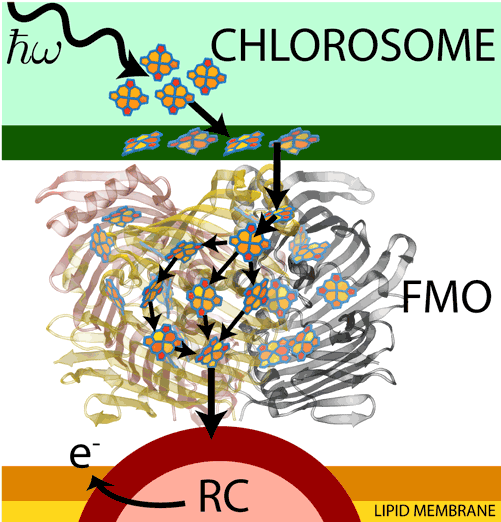Fig 1: Light absorbed by pigment molecules in the chlorosome is passed through
FMO to the reaction center (RC), where it is used to eject an electron, creating a
charge gradient.
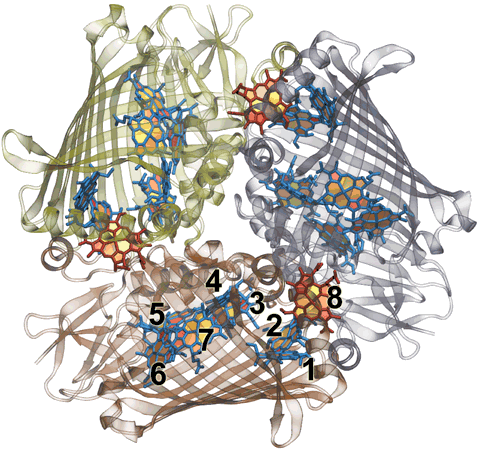Fig 2: FMO homo-trimer from Chlorobaculum tepidem. Each monomer
sandwiches 7 bacteriochlorophyll molecules for light harvesting. Between each
monomomer there is an additional 8th bacteriochlorophyll to make a total of 24
for the trimer. The conventional numbering scheme is shown.Green sulphur bacteria harvest sunlight by absorbing solar energy in large pigment-containing vesicles known as a chlorosomes and transporting this energy to a reaction center for charge separation (detailed in Fig. 1). Along the way, excitation absorbed by the chlorosome is passed through the Fenna-Matthews-Olson (FMO) complex (Fig. 2) to get to the reaction center complex. As this process occurs in a biological environment, there is a significant amount of thermal noise present. As excitation is passed between pigments, from the bacteriochlorophylls (BChls) in the chlorosome to those in FMO and finally to those in the reaction center (RC), it is constantly under the influence of thermal fluctuations. It is of importance then that FMO can efficiently conduct excitation energy, i.e., without much energy loss. One way to do this could be by exploiting quantum coherence to speed up energy transfer.
Quantum Coherence in FMO
The Fenna-Matthews-Olson (FMO) complex has been the subject of many recent studies. This is in part due to experimenters observing unexpected quantum phenomena at ambient temperatures. The has been much debate about how quantum coherent beating can exist in the presence of a noisy environment, such as a living cell. Theoretical investigations of excitation dynamics in FMO have furnished similar beating signals and offered some understanding of what is going on in FMO. There remains many questions to answer still: are the experimental signals due to correlated noise effects? how accurate are the present models of the protein environment? what does the excitation dynamics look like with an improved model of the environment? The combination of molecular dynamics and quantum chemistry calculations provide a great tool to attack these questions with.
A molecular dynamics simulation explicitly calculates the fluctuations of all the different parts of the system. Each simulation step can thus be used to perform a calculation of the BChl excited states energies and interactions in the presence of thermal disorder. This provides us with a time dependent Hamiltonian describing the singly excited BChl subsystem - exactly what is needed to calculate excitation dynamics as influenced by a realistic environment
Simulation procedure
We equilibrated the FMO trimer from Chlorobaculum tepidem (PDB code 3ENI) under standard conditions. This contained a monomer of the homo-trimer with 8 BChls bound. After equilibration, the simulation was run for 300 ps, saving snapshots every 5 fs. Each snapshot was used to determine the excite state energy of each BChl using the ZINDO/S method. The interaction between the excited states were calculated using the TrEsp approach (calculating the interaction between atomic partial charge distributions corresponding to the excited state for each BChl). The resulting Hamiltonian of energy levels and interactions was used for calculating BChl correlation, and excitation dynamics and spectra of FMO.
Results
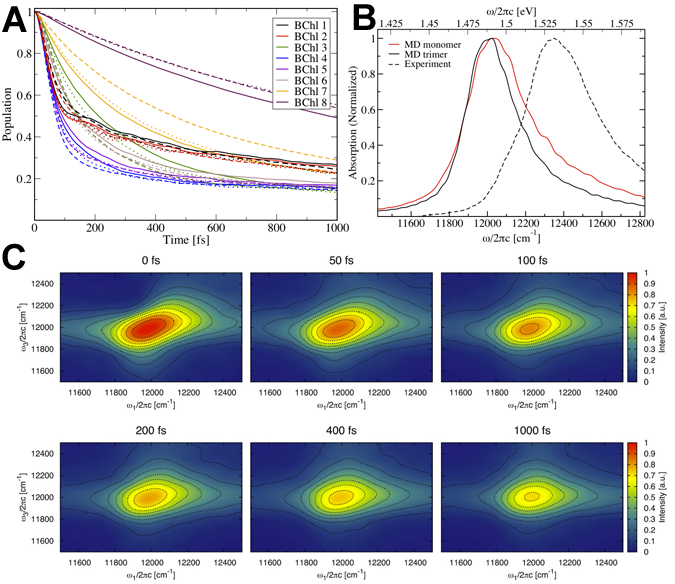Fig 3: (A) Excitation dynamics of BChls 1-8 (B) Linear absorption spectrum (C) 2D absorption spectrum. Despite reasonable reproduction of the linear absorption spectrum, we see no coherent beating in the excitation dynamics or the 2D spectra of FMO. (click on image for higher resolution)
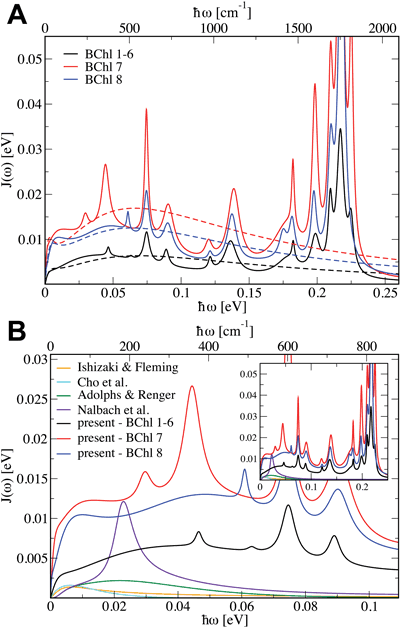Fig 4: (A) Spectral density of FMO BChls with bi-exponential fits shown as dashed lines. (B) Comparison of current spectral density with prior results. (click on image for higher resolution)No Correlated Fluctuations
It was suggested that long-lived coherent beating could arise if the thermal fluctutations of different pigments in the complex were correlated. I.e., if the fluctuations of the excited state energy of two pigmets were correlated. Our MD simulation showed (see Olbrich et al., Quest for Spatially Correlated Fluctuations in FMO, JPCB, 2011), however, that there was no correlation between the fluctuations of the excited state energies. We did find that the excited state coupling terms were corredlated to some extent, if they shared a common BChl. I.e. The fluctuations of couplings 1-2 and 2-3 are correlated to some extent. This correlation has little influence on excitation dynamics, though, as the fluctuations in the couplings are an order of magnitude smaller than the fluctuations of the excited state energies.
Excitation Dynamics and Absorption Spectra
The Hamiltonian calculated using the ZINDO/S method for FMO was presented in Olbrich et al., Exciton Dynamics and 2D Spectra of FMO, JPCB 2011. From this (time-dependent) Hamiltonian, we calculated the excited state dynamics in the forms of the excited state population decay from each BChl, the linear absorption spectrum and 2D absorption spectrum (see Fig. 3). Although the overall shape is similar, the calculated linear absorption spectrum is shifted by -40 meV and 15% narrower than the experimental spectrum. These differences are likely due to assumptions in the MD methodology, particularly the assumption of static charge distributions in the molecules and underestimation of site energies from ZINDO/S. In neither the excitation dynamics nor the 2D spectra do we see coherent oscillations as reported in recent investigations.
Environmental Influence
The time dependent Hamiltonian allows the calculation of the spectral density for each BChl in FMO. The spectral density is the key determinant of environmental influence in many methods that calculate excitation dynamics. It represents the averaged influence of each fluctuating mode in the environment on the excited state energy, thus determining how the excited state populations and coherences are affected by thermal noise. Using the autocorrelation functions of the excited state energies (i.e., the diagonal entries in the Hamiltonian) we determined the spectral density for each BChl in FMO (see Fig. 4), presented in Olbrich et al., Theory and Simulation of Environmental Effects on FMO Electronic Transitions, JPCLett., 2011.
We see that the BCHls of FMO can be separated into three different groups: the low-noise group comprising most of the BChls and the two higher-noise groups each containing only one BChl, namely BChls 7 and 8 that are situation in the center of each monomer and between monomers, respectively. Comparing our results with prior work we see significantly stronger coupling between the environmental and BChl excited states. This stronger coupling may explain why we didn’t see coherent beating signals (Fig. 3) but this explanation is hampered by the narrower absorption spectrum (indicating the need for more noise such as static disorder).
All work was carried out in collaboration with Ulrich Kleinekathoefer and his students (website) at the Jacob’s University in Bremen, Germany.
Publications
Methods and results are presented in the following publications:Related TCB Group Projects
Page created and maintained by Johan Strümpfer.
