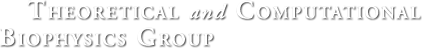Flagellin Translocation and Flagellum Growth
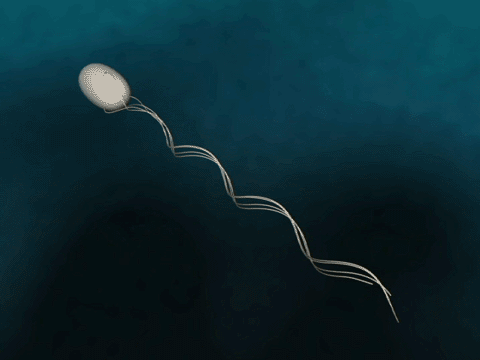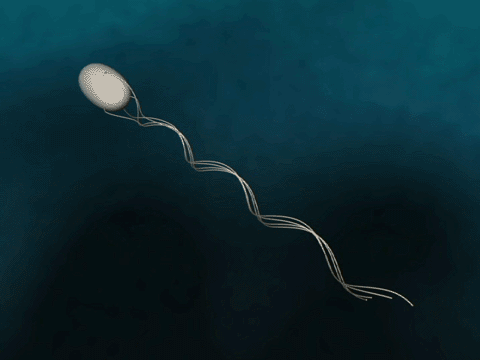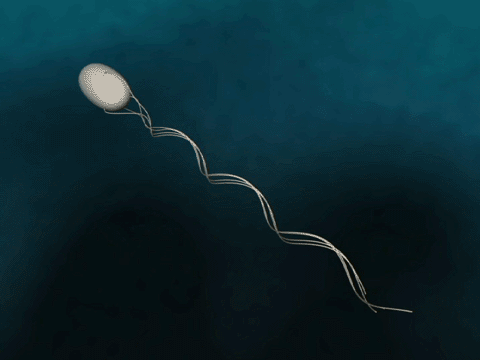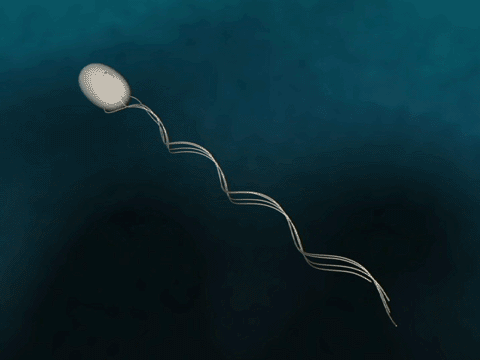
Flagellar Propulsion The bacterial flagellum is a several micrometer long filament which bacteria use for swimming. The flagellum consists of a base, filament and cap. In the base, which binds the flagellum to the bacterium, a proton gradient driven motor rotates the filament helically for propulsion. The cap is explained below. |
Flagellum Structure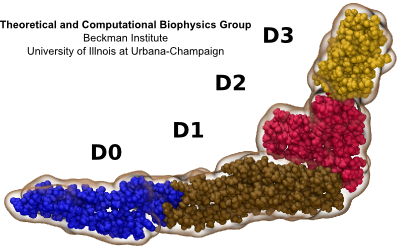
Fig. 2 Four domains of flagellin. 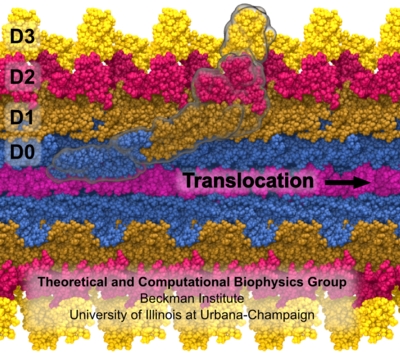
Fig. 3 Flagellum is built from helically stacked flagellins. Domain D0 (blue) comprises the channel which confines translocating flagellin (magenta). The flagellum [Namba et al. (1989)] is built from repeating flagellin monomers which stack helically. Each repeat of 11 flagellin monomers adds 52 Å to the length of the flagellum. Flagellin (Fig. 2) has four domains, D0 (blue), D1 (brown), D2 (red) and D3 (gold), which represent distance from the center of the filament. Domain D0 is the inner most domain and comprises the inner surface of the flagellar channel (Fig. 3). This channel, only 20 Å in diameter, is so narrow that it only conducts unfolded flagellin. |
Flagellin Translocation leads to Flagellar Growth
Fig. 4 Cap assists flagellin to fold into place at tip. 
Fig. 5 Self Assembly. Flagellin is pumped into channel at the base and translocates to tip where it folds into place, thereby elongating flagellum. At the base of the flagellum, a type III secretion system pumps unfolded flagellin monomers into the flagellum's central channel. Each flagellin pushes its distal neighbor toward the tip. When a flagellin reaches the tip, the cap protein [Maki‑Yonekura et al. (2003)] helps it to properly fold into place, thereby elongating the flagellum. The filament growth rate, V(L), which depends on filament length, is known to decay exponentially with length according to V(L) = V0 exp(-L/a) , where V0 (roughly 9 nm/s) is the growth rate of nascent flagella and a (roughly 3.7 μm) is the exponential decay length [Iino (1974)]. Our research explains how structural biophysics, theoretical modeling and molecular dynamics simulation combine to explain how the physical properties of the flagellin translocation system cause the flagellum growth rate to exponentially decay with length. |
Theoretical Model of Flagellin Translocation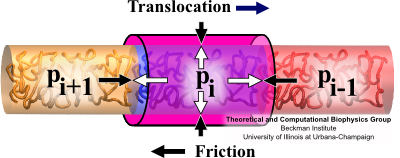
Fig. 6 Forces on segment of translocating flagellin: proximal neighbor pressure, distal neighbor pressure, friction and channel confinement. The rate at which the flagellum grows stems from the rate at which flagellin monomers can translocate through the confining channel. The rate of translocation depends on properties of the pump, cap and flagellin/channel friction interactions. Though these processes and interactions are very complicated, our simplified model of flagellin translocation gives a correct, and very clear, understanding of the translocation and growth process. We describe translocating flagellin through 6 position dependent properties:
|
Biological Conditions
Fig. 7 Simulating confined flagellin. Two types of simulations were performed of flagellin confined to a cylinder; in both, a segment of flagellin was cylindrically confined by a spring-like force to a specific radius. The axial force (black) differs between simulation types. During these simulations, pressure, density and friction contacts are measured. Compression. The position of the harmonic force which axially confines the flagellin slowly moves inward from xa at t=t0 (blue) to xb at t=tf (red) Equilibration. The position of the harmonic forces which axially confine the flagellin remains fixed during the simulation. Several biological conditions in the flagellum combine to setup a boundary value differential equation which can be solved for flagellin pressure as a function of positions. Additional conditions allow the remaining flagellin properties to be derrived from flagellin pressure. Condition 1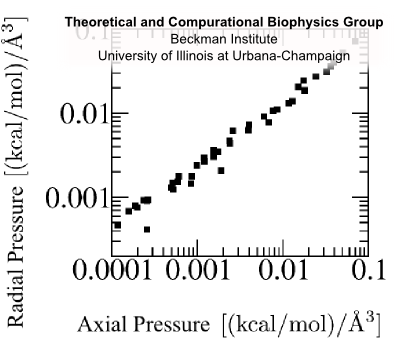
Fig. 8 Isotropic pressure. For equilibrium simulations (Fig. 7) at several channel radii and lengths, radial and axial pressure are equal. Flagellin pressure, p, is isotropic. Refering to Fig. 6, radial pressure (up/down white arrows) which an unfolded flagellin exerts against the channel surface (magenta) should be equal to the axial pressure (left/right white arrows) which the flagellin exerts on its proximal (gold) and distal (red) neighbors. Justification We expect that a denatured protein, a self-avoiding but otherwise rather flexible polymer, possesses this property typical for a fluid and does relay compression, exerted on it axially, also radially (Fig. 6). Molecular dynamics simulations of flagellin confined in a cylinder (Fig. 7), allowed measurement of radial and axial pressure; comparison (Fig. 8) shows that the pressure of a denatured flagellin monomer is isotropic. |
Condition 2Friction density, g, is proportional to flagellin pressure, p. Refering to Fig. 6, friction per unit surface area (magenta) equals the product of a coefficient of friction and the normal force, i.e. the pressure; p = α g. Justification It is intuitive that increasing flagellin pressure will increase friction. It is not, however, intuitive that friction should be velocity independent. This model of friction appears to contradict fundamental models of friction, such as velocity dependent fluid friction. Our model is supported by recent studies of "creeping static friction" [Muser (2008)]. Creeping friction is static friction, meaning the applied forces are not sufficient to induce dynamic friction, yet very slow translocation ensues. At these low forces, flagellin is only able to creep along at very slow velocities; velocities of creeping static friction are so small that they were only recently measurable and are on the same order of magnitude of flagellin translocation velocities (1 nm/ms). Condition 3Translocating flagellin is in mechanical equilibrium. The velocity of translocation is so slow, ~1nm/ms, that the flagellin is in mechanical equilibrium; this means that the forces along the channel sum to zero. Justification Because translocation is so slow, it is quite reasonable that flagellin is able to sample all of its local conformations and remain in equilibrium during translocation. Condition 4
Fig. 9 ftip derives from the force required to push a flagellin past the cap protein then fold into place. Flagellin pressure at the flagellar tip is ftip/πR² where ftip is the force with which flagellin has to push past the cap to exit the channel (Fig. 9); this force is flagellum length independent. Justification Because translocation is so slow, it is quite reasonable that flagellin is able to sample all of its local conformations and remain in equilibrium during translocation. These conditions setup a boundary value differential equation which is easily solved for: p(x) = (ftip/πR²) exp[(2α/R)x] and, thanks to Condition 2, g(x) = (ftipα/πR²) exp[(2α/R)x] Condition 5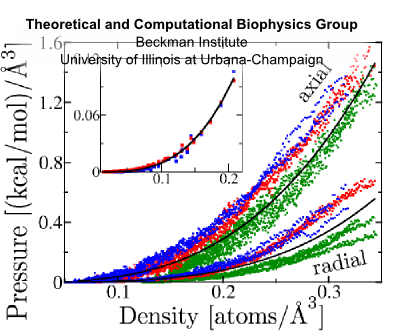
Fig. 10 Flagellin pressure vs. density for compression and equilibrium (inset) simulations; fit to p = γ (ρ/ρ0)β (black):
Flagellin pressure is a power law function of density. This relationship bears the form p = γ(ρ/ρ0)β For β = 1 this ammounts to the ideal gas law; for proteins with additional inter-atomic forces and chemical bonds, we expect β > 1. Justification Modeling unfolded flagellin in the flagellum as a Gaussian chain confined to a cylinder, the pressure density relationship is described as p = c1ρ + c2ρ³ where the second term is 1-2 orders of magnitude larger, giving p = γ (ρ/ρ0)³. Simulations of flagellin being compressed in cylinders confirms that β ≈ 3 (Fig 10). This additional relationship allows us to express density from pressure: ρ(x) = ρ0(ftip/γπR²)1/β exp[(2α/Rβ)x] Condition 6Flagellin monomers are pumped into the channel as a constant power, P. This boundary condition gives a relationship between pressure and velocity at the base of the channel. Justification This holds true for biological pumps, which operate by ATP hydrolysis at some fixed rate and have been shown to slow down under increasing load [Chemla et al. (2005)]. With this condition, we can express flagellin flux as φ(L) = ρ0(P/ftip)(ftip/γπR²)1/β exp[(2α/R)(1/β-1)L] and flagellin translocation velocity as v(x,L) = (P/ftip) exp{-(2α/R)[L-(L-x)/β]} Flagellum Growth RateBy considering that the additional length which each flagellin contributes the flagellum, λ = 5Å/flagellin we can express the growth rate of the flagellum in terms of flagellin flux as V = λπR²φ which evauates to V(L) = V0 exp(-L/a) where the growth rate of nascent flagella is V0 = λρ0(PπR²/ftip)(ftip/γπR²)1/β and the growth rate decay length is a = (R/2α)/(1-1/β) It is remarkable that this simple model of flagellin translocation reproduces the exponential decay of growth with filament length seen from experiment. Because our model is based on physical properties of the system, the we have elucidated how the growth rate parameters, V0 and a, are based on system properties, λ, P, R, ftip, γ, β and α. |
Implications for Flagellar Growth
Fig. 11 Flagellin translocation simulation. Click here for movie. These expressions offer a wealth of insight into flagellin translocation through the long, confining flagellar channel and why the growth rate decays exponentially with length. As the flagellum grows, flagellin density at the base increases (see ρ(x)). As a result, friction at the base grows (see g(x)). Increasing friction causes pressure to increase at the base (see p(x)). Since the secretion system operates at constant power, the increasing pressure required to pump in flagellin at the base means that the rate of insertion must decrease proportionally, thereby slowing the rate of translocation and, consequently, filament growth. When the injection force of the pump reaches its stall force, elongation ceases and the flagellum has reached its maximal length ,Lmax = (R/2α) ln(fstall/ftip). We see here that the maximal length of the flagellum depends only logarithmically on fstall, and it depends linearly on the coefficient translocation friction, α. Future simulation and exploration of flagellin translocation will give further insight into the nature of translocation and friction and their dependencis on the channel structure. PublicationsTheoretical and computational investigation of flagellin translocation and bacterial flagellum growth. David E. Tanner, Wen Ma, Zhongzhou Chen, and Klaus Schulten. Biophysical Journal, 2011. In press. InvestigatorsRelated TCB Group ProjectsPage created and maintained by David E. Tanner. |