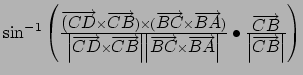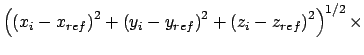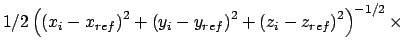



Next: Adaptive Biasing Force Calculations
Up: Additional Simulation Parameters
Previous: Applied Forces and Analysis
Contents
Index
Subsections
Free Energy of Conformational Change Calculations
NAMD incorporates methods for performing free energy of conformational change perturbation calculations.
The system is efficient if only a few coordinates, either of individual atoms or centers of mass of groups of atoms, are needed.
The following configuration parameters are used to enable free energy perturbation:
The following sections describe the format of the free energy perturbation script.
These restraints extend the scope of the available restraints beyond that
provided by the harmonic position restraints. Each restraint is imposed with
a potential energy term, whose form depends on the type of the
restraint.
Fixed Restraints
Position restraint (1 atom): force constant 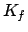 , and reference
position
, and reference
position
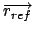
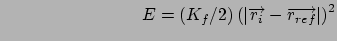
Stretch restraint (2 atoms): force constant 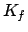 , and reference
distance
, and reference
distance 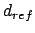
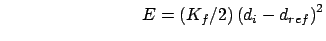
Bend restraint (3 atoms): force constant 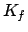 , and reference angle
, and reference angle 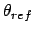
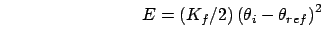
Torsion restraint (4 atoms): energy barrier 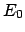 , and reference
angle
, and reference
angle 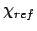
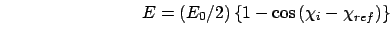
Forcing restraints
Position restraint (1 atom): force constant 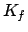 , and two reference
positions
, and two reference
positions
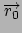 and
and
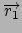
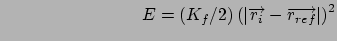

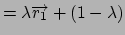
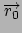
Stretch restraint (2 atoms): force constant 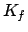 , and two reference
distances
, and two reference
distances 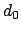 and
and 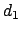
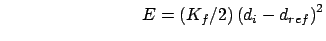
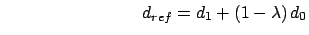
Bend restraint (3 atoms): force constant 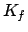 , and two reference
angles
, and two reference
angles 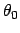 and
and 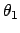
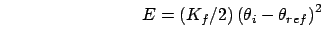
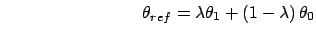
Torsion restraint (4 atoms): energy barrier E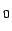 , and two reference
angles
, and two reference
angles 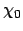 and
and 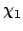
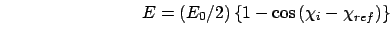
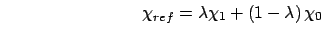
The forcing restraints depend on the coupling parameter,  ,
specified in a conformational forcing calculation. For example, the
restraint distance,
,
specified in a conformational forcing calculation. For example, the
restraint distance, 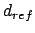 , depends on
, depends on  , and as
, and as  changes two atoms or centers-of-mass are forced closer together or further
apart. In this case
changes two atoms or centers-of-mass are forced closer together or further
apart. In this case 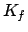 =
= 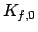 , the value supplied at input.
, the value supplied at input.
Alternatively, the value of 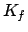 may depend upon the coupling parameter
may depend upon the coupling parameter
 according to:
according to:
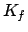 =
=
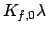
Bounds
| Position bound (1 atom): |
Force constant 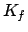 , reference position , reference position
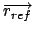 , , |
| |
and upper or lower reference distance, 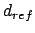 |
Upper bound:
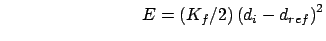 for
for 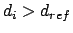 , else
, else 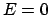 .
.
Lower bound:
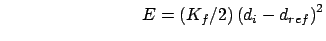 for
for 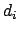
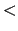
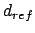 , else
, else 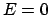 .
.
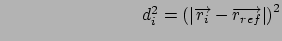
| Distance bound (2 atoms): |
Force constant 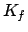 , , |
| |
and upper or lower reference distance, 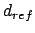 |
Upper bound:
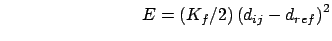 for
for
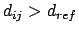 , else
, else 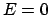 .
.
Lower bound:
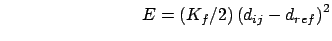 for
for
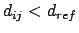 , else
, else 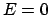 .
.
| Angle bound (3 atoms): |
Force constant 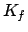 , , |
| |
and upper or lower reference angle, 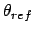 |
Upper bound:
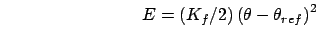 for
for
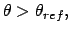 else
else 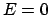 .
.
Lower bound:
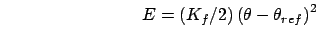 for
for
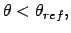 else
else
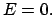
| Torsion bound (4 atoms): |
An upper and lower bound must be provided
together. |
| |
Energy gap 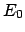 , lower AND upper reference angles, , lower AND upper reference angles, 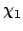 and and 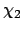 , , |
| |
and angle interval, 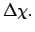 |
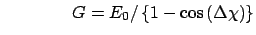
Bounds may be used in pairs, to set a lower and upper bound. Torsional
bounds always are defined in pairs.
Conformational forcing / Potential of mean force
In conformational forcing calculations, structural parameters such as atomic
positions, inter-atomic distances, and dihedral angles are forced to change
by application of changing restraint potentials. For example, the distance
between two atoms can be restrained by a potential to a mean distance that
is varied during the calculation. The free energy change (or potential of
mean force, pmf) for the process can be estimated during the simulation.
The potential is made to depend on a coupling parameter,  , whose
value changes during the simulation. In potential of mean force
calculations, the reference value of the restraint potential depends on
, whose
value changes during the simulation. In potential of mean force
calculations, the reference value of the restraint potential depends on  . Alternately, the force constant for the restraint potential may
change in proportion to the coupling parameter. Such a calculation gives the
value of a restraint free energy, i.e., the free energy change of the
syste
. Alternately, the force constant for the restraint potential may
change in proportion to the coupling parameter. Such a calculation gives the
value of a restraint free energy, i.e., the free energy change of the
syste
m due to imposition of the restraint potential.
Methods for computing the free energy
With conformational forcing (or with molecular transformation calculations)
one obtains a free energy difference for a process that is forced on the
system by changing the potential energy function that determines the
dynamics of the system. One always makes the changing potential depend on a
coupling parameter,  . By convention,
. By convention,  can have values
only in the range from
can have values
only in the range from 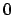 to
to 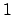 , and a value of
, and a value of 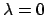 corresponds
to one defined state and a value of
corresponds
to one defined state and a value of 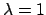 corresponds to the other
defined state. Intermediate values of
corresponds to the other
defined state. Intermediate values of  correspond to intermediate
states; in the case of conformational forcing calculations these
intermediate states are physically realizable, but in the case of molecular
transformation calculations they are not.
correspond to intermediate
states; in the case of conformational forcing calculations these
intermediate states are physically realizable, but in the case of molecular
transformation calculations they are not.
The value of  is changed during the simulation. In the first
method provided here, the change in
is changed during the simulation. In the first
method provided here, the change in  is stepwise, while in the
second method it is virtually continuous.
is stepwise, while in the
second method it is virtually continuous.
Multi-configurational thermodynamic integration (MCTI).
In MCTI one accumulates
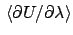 at several values of
at several values of  , and from these averages
estimates the integral
, and from these averages
estimates the integral
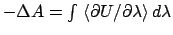
With this method, the precision of each
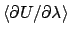 can be estimated from the fluctuations of the time
series of
can be estimated from the fluctuations of the time
series of
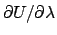 .
.
Slow growth.
In slow growth,  is incremented by
is incremented by
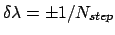 after each dynamics integration time-step, and the pmf is estimated as
after each dynamics integration time-step, and the pmf is estimated as
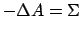
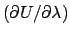
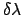
Typically, slow growth is done in cycles of: equilibration at 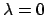 ,
change to
,
change to 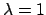 , equilibration at
, equilibration at 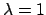 , change to
, change to 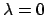 . It is usual to estimate the precision of slow growth simulations from the
results of successive cycles.
. It is usual to estimate the precision of slow growth simulations from the
results of successive cycles.
User-supplied restraint and bounds specifications
urestraint 
n * (restraint or bound specification) //
see below
Restraint Specifications (not coupled to pmf calculations)
| posi |
ATOM |
kf = KF |
ref = (X Y Z) |
| dist |
2 x ATOM |
kf = KF |
ref = D |
| angle |
3 x ATOM |
kf = KF |
ref = A |
| dihe |
4 x ATOM |
barr = B |
ref = A |
Bound Specifications (not coupled to pmf calculations)
| posi bound |
ATOM |
kf = KF |
[low = (X Y Z D) or hi = (X Y Z D)] |
| dist bound |
2 x ATOM |
kf = KF |
[low = D or hi = D] |
| angle bound |
3 x ATOM |
kf = KF |
[low = A or hi = A] |
| dihe bound |
4 x ATOM |
gap = E |
low = A0 hi = A1 delta = A2 |
Forcing Restraint Specifications (coupled to pmf calculations)
| posi pmf |
ATOM |
kf=KF |
low = (X0 Y0 Z0) hi = (X1 Y1 Z1) |
| dist pmf |
2 x ATOM |
kf=KF |
low = D0 hi = D1 |
| angle pmf |
3 x ATOM |
kf=KF |
low = A0 hi = A1 |
| dihe pmf |
4 x ATOM |
barr=B |
low = A0 hi = A1 |
Units
| Input item |
Units |
| E, B |
kcal/mol |
| X, Y, Z, D |
|
| A |
degrees |
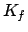 |
kcal/(mol 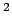 ) or kcal/(mol rad ) or kcal/(mol rad ) ) |
The designation ATOM, above, stands for one of the following forms:
A single atom
(segname, resnum, atomname)
Example: (insulin, 10, ca)
All atoms of a single residue
(segname, resnum)
Example: (insulin, 10)
A list of atoms
group  (segname, resnum, atomname), (segname, resnum, atomname),
(segname, resnum, atomname), (segname, resnum, atomname), 

Example: group  (insulin, 10, ca), (insulin, 10, cb), (insulin,
11, cg)
(insulin, 10, ca), (insulin, 10, cb), (insulin,
11, cg) 
All atoms in a list of residues
group  (segname, resnum), (segname, resnum),
(segname, resnum), (segname, resnum), 

Example: group  (insulin, 10), (insulin, 12), (insulin, 14)
(insulin, 10), (insulin, 12), (insulin, 14) 
All atoms in a range of residues
group  (segname, resnum) to (segname, resnum)
(segname, resnum) to (segname, resnum) 
Example: group  (insulin, 10) to (insulin, 12)
(insulin, 10) to (insulin, 12) 
One or more atomnames in a list of residues
group  atomname: (segname, resnum), (segname, resnum), atomname: (segname, resnum), (segname, resnum),   |
group  (atomname, atomname, (atomname, atomname,  ): (segname, resnum), (segname,
resnum), ): (segname, resnum), (segname,
resnum),   |
| Examples: |
group  ca: (insulin, 10), (insulin, 12), (insulin, 14) ca: (insulin, 10), (insulin, 12), (insulin, 14)
 |
| |
group  (ca, cb, cg): (insulin, 10), (insulin, 12), (insulin, 14) (ca, cb, cg): (insulin, 10), (insulin, 12), (insulin, 14)  |
| |
group  (ca, cb): (insulin, 10), (insulin, 12) cg: (insulin, 11),
(insulin, 12) (ca, cb): (insulin, 10), (insulin, 12) cg: (insulin, 11),
(insulin, 12)  |
Note: Within a group, atomname is in effect until a new atomname is
used, or the keyword all is used. atomname will not carry over from group to
group. This note applies to the paragraph below.
One or more atomnames in a range of residues
group  atomname: (segname, resnum) to (segname, resnum) atomname: (segname, resnum) to (segname, resnum)  |
group  (atomname, atomname, (atomname, atomname,  ): (segname, resnum) to (segname,
resnum) ): (segname, resnum) to (segname,
resnum)  |
| Examples: |
group  ca: (insulin, 10) to (insulin, 14) ca: (insulin, 10) to (insulin, 14)  |
| |
group  (ca, cb, cg): (insulin, 10) to (insulin, 12) (ca, cb, cg): (insulin, 10) to (insulin, 12)  |
| |
group  (ca, cb): (insulin, 10) to (insulin, 12) all: (insulin, 13) (ca, cb): (insulin, 10) to (insulin, 12) all: (insulin, 13)  |
The pmf and mcti blocks, below, are used to simultaneously control all
forcing restraints specified in urestraint above. These blocks are performed
consecutively, in the order they appear in the config file. The pmf block is
used to either a) smoothly vary  from 0
from 0  1 or 1
1 or 1  0, or b) set lambda. The mcti block is used to vary
0, or b) set lambda. The mcti block is used to vary  from 0
from 0 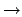 1 or 1
1 or 1 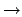 0 in steps, so that
0 in steps, so that  is
fixed while
is
fixed while 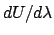 is accumulated.
is accumulated.
Lamba control for slow growth
pmf 
task = [up, down, stop, grow, fade, or nogrow]
time = T [fs, ps, or ns] (default = ps)
lambda = Y (value of  ; only needed for stop and nogrow)
; only needed for stop and nogrow)
lambdat = Z (value of 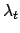 ; only needed for grow, fade, and
nogrow) (default = 0)
; only needed for grow, fade, and
nogrow) (default = 0)
print = P [fs, ps, or ns] or noprint (default = ps)
Lambda control for automated MCTI
mcti 
task = [stepup, stepdown, stepgrow, or stepfade]
equiltime = T1 [fs, ps, or ns] (default = ps)
accumtime = T2 [fs, ps, or ns] (default = ps)
numsteps = N
lambdat = Z (value of 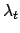 ; only needed for stepgrow, and
stepfade) (default = 0)
; only needed for stepgrow, and
stepfade) (default = 0)
print = P [fs, ps, or ns] or noprint (default = ps)
For each task,  changes in steps of (1.0/N) from 0
changes in steps of (1.0/N) from 0  1
or 1
1
or 1  0. At each step, no data is accumulated for the initial
period T1, then dU/d
0. At each step, no data is accumulated for the initial
period T1, then dU/d is accumulated for T2. Therefore, the total
duration of an mcti block is (T1+T2) x N.
is accumulated for T2. Therefore, the total
duration of an mcti block is (T1+T2) x N.
Fixed restraints
| // 1. restrain the position of the ca atom of residue 0. |
| // 2. restrain the distance between the ca's of residues 0
and 10 to 5.2Å |
// 3. restrain the angle between the ca's of residues 0-10-20
to 90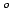 . . |
// 4. restrain the dihedral angle between the ca's of
residues 0-10-20-30 to 180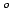 . . |
// 5. restrain the angle between the centers-of-mass of
residues 0-10-20 to 90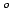 . . |
urestraint 
posi (insulin, 0, ca) kf=20 ref=(10, 11, 11)
dist (insulin, 0, ca) (insulin, 10, ca) kf=20 ref=5.2
angle (insulin, 0, ca) (insulin, 10, ca) (insulin, 20, ca) kf=20 ref=90
dihe (insulin, 0, ca) (insulin, 10, ca) (insulin, 20, ca) (insulin, 30,
ca) barr=20 ref=180
angle (insulin, 0) (insulin, 10) (insulin, 20) kf=20 ref=90
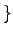
| // 1. |
restrain the center of mass of three
atoms of residue 0. |
| // 2. |
restrain the distance between (the
COM of 3 atoms of residue 0) to (the COM of 3 atoms of residue 10). |
| // 3. |
restrain the dihedral angle of
(10,11,12)-(15,16,17,18)-(20,22)-(30,31,32,34,35) to 90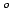 |
| // |
( (ca of 10 to 12), (ca, cb, cg of 15 to
18), (all atoms of 20 and 22), (ca of 30, 31, 32, 34, all atoms of 35) ). |
urestraint 
posi group  (insulin, 0, ca), (insulin, 0, cb), (insulin, 0, cg)
(insulin, 0, ca), (insulin, 0, cb), (insulin, 0, cg) kf=20 ref=(10, 11, 11)
kf=20 ref=(10, 11, 11)
| dist |
group  (insulin, 0, ca), (insulin, 0, cb), (insulin, 0, cg) (insulin, 0, ca), (insulin, 0, cb), (insulin, 0, cg) |
| |
group  (insulin, 10, ca), (insulin, 10, cb), (insulin, 10, cg) (insulin, 10, ca), (insulin, 10, cb), (insulin, 10, cg) kf=20 ref=6.2
kf=20 ref=6.2 |
| dihe |
group  ca: (insulin, 10) to (insulin, 12) ca: (insulin, 10) to (insulin, 12) |
| |
group  (ca, cb, cg): (insulin, 15) to (insulin, 18) (ca, cb, cg): (insulin, 15) to (insulin, 18) |
| |
group  (insulin, 20), (insulin, 22) (insulin, 20), (insulin, 22) |
| |
group  ca: (insulin, 30) to (insulin, 32), (insulin, 34), all:
(insulin, 35) ca: (insulin, 30) to (insulin, 32), (insulin, 34), all:
(insulin, 35) barr=20 ref=90 barr=20 ref=90 |

Bound specifications
| // 1. |
impose an upper bound if an atom's
position strays too far from a reference position. |
| // |
(add an energy term if the atom is more
than 10Å from (2.0, 2.0, 2.0) ). |
| // 2&3. |
impose lower and upper bounds on
the distance between the ca's of residues 5 and 15. |
| // |
(if the separation is less than 5.0Å
or greater than 12.0Å add an energy term). |
| // 4. |
impose a lower bound on the angle
between the centers-of-mass of residues 3-6-9. |
| // |
(if the angle goes lower than 90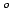 apply a restraining potential).
apply a restraining potential). |
urestraint 
posi bound (insulin, 3, cb) kf=20 hi = (2.0, 2.0, 2.0, 10.0)
dist bound (insulin, 5, ca) (insulin, 15, ca) kf=20 low = 5.0
dist bound (insulin, 5, ca) (insulin, 15, ca) kf=20 hi = 12.0
angle bound (insulin, 3) (insulin, 6) (insulin, 9) kf=20 low=90.0
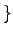
| // torsional bounds are defined as pairs. this example
specifies upper and lower bounds on the |
// dihedral angle, 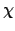 , separating the
planes of the 1-2-3 residues and the 2-3-4 residues. , separating the
planes of the 1-2-3 residues and the 2-3-4 residues. |
| // The energy is 0 for: |
-90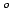 |
< 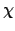 |
< 120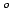 |
| // The energy is 20 kcal/mol for: |
130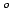 |
< 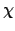 |
< 260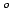 |
// Energy rises from 0 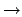 20
kcal/mol as 20
kcal/mol as 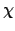 increases from 120 increases from 120
 130
130 , and decreases from -90 , and decreases from -90
 -100 -100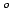 . . |
urestraint 
dihe bound (insulin 1) (insulin 2) (insulin 3) (insulin 4) gap=20 low=-90
hi=120 delta=10

Forcing restraints
| // a forcing restraint will be imposed on the distance
between the centers-of-mass of residues (10 to 15) and |
// residues (30 to 35). low=20.0, hi=10.0, indicates that the
reference distance is 20.0at  =0, and 10.0at =0, and 10.0at  =1. =1. |
urestraint 
| dist pmf |
group  (insulin, 10) to (insulin, 15) (insulin, 10) to (insulin, 15)  |
| |
group  (insulin, 30) to (insulin, 35) (insulin, 30) to (insulin, 35)  kf=20,
low=20.0, hi=10.0 kf=20,
low=20.0, hi=10.0 |
// 1. during the initial 10 ps, increase the strength of the
forcing restraint to full strength: 0 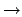 20
kcal/(mol 20
kcal/(mol 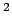 ) ) |
// 2. next, apply a force to slowly close the distance from
20 to 10 ( changes from 0 changes from 0 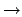 1) 1) |
// 3. accumulate dU/d for another
10 ps. ( stays fixed at 1) for another
10 ps. ( stays fixed at 1) |
// 4. force the distance back to its initial value of 20
( changes from 1 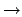 0) 0) |
pmf 
task = grow
time = 10 ps
print = 1 ps

pmf 
task = up
time = 100 ps

pmf 
task = stop
time = 10 ps

pmf 
task = down
time = 100 ps
| // 1. |
force the distance to close from 20
to 10 in 5 steps. ( changes from 0 changes from 0 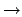 1: 0.2, 0.4, 0.6, 0.8, 1.0)
1: 0.2, 0.4, 0.6, 0.8, 1.0) |
| // |
at each step equilibrate for 10 ps,
then collect dU/d for another 10 ps. for another 10 ps. |
| // |
ref = 18, 16, 14, 12, 10
, duration = (10 + 10) x 5 = 100 ps. |
| // 2. |
reverse the step above ( changes from 1
changes from 1 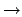 0: 0.8,
0.6, 0.4, 0.2, 0.0) 0: 0.8,
0.6, 0.4, 0.2, 0.0) |
mcti 
task = stepup
equiltime = 10 ps
accumtime = 10 ps
numsteps = 5
print = 1 ps

mcti 
task = stepdown

Gradient for position restraint
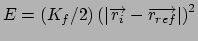
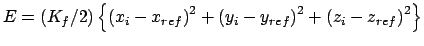
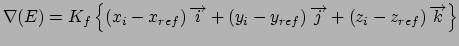
Gradient for stretch restraint
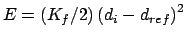
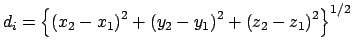
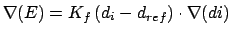
for atom 2 moving, and atom 1 fixed
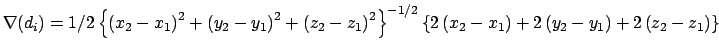
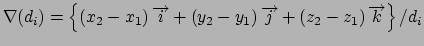
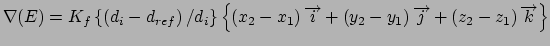
Gradient for bend restraint
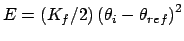
Atoms at positions A-B-C
distances: (A to B) = c; (A to C) = b; (B to C) = a;
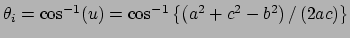
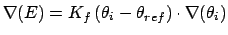
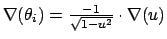
for atom A moving, atoms B & C fixed (distances b and c
change)
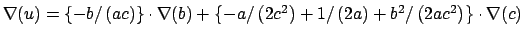
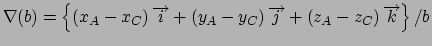
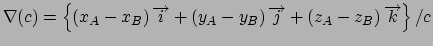
for atom B moving, atoms A & C fixed (distances a and c
change)
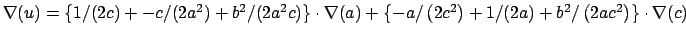
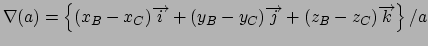
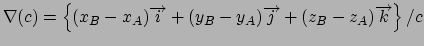
for atom C moving, atoms A & B fixed (distances a and b
change)
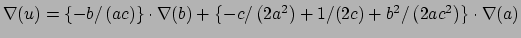
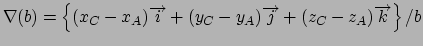
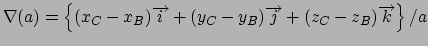
Gradient for dihedral angle restraint
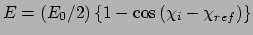
Atoms at positions A-B-C-D
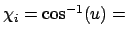
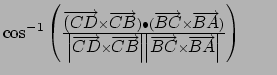 AND
AND
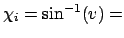
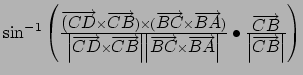
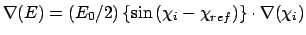
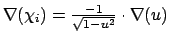
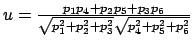
for atom A moving, atoms B, C, & D fixed
for atom B moving, atoms A, C, & D fixed
Gradient for forcing position restraint
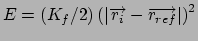
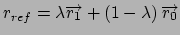
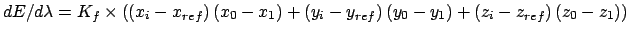
Gradient for forcing stretch restraint
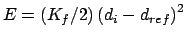
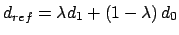
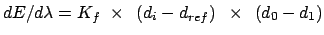
Gradient for forcing bend restraint
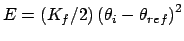
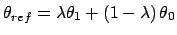
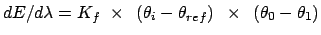
Gradient for forcing dihedral restraint
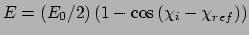
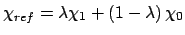
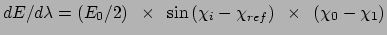




Next: Adaptive Biasing Force Calculations
Up: Additional Simulation Parameters
Previous: Applied Forces and Analysis
Contents
Index
namd@ks.uiuc.edu
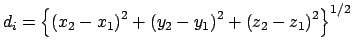
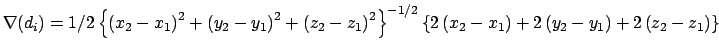
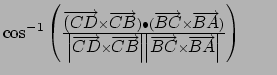 AND
AND