

Next: Semi-empirical parameter generation: SPARTAN
Up: VMD Tutorial
Previous: The CHARMM22 Force Field
Subsections
We now have a nonstandard amino acid side group attached
to the hisH protein. As is very often the case with nonstandard
groups, this residue does not have a full set of parameters
describing it.When presented with a nonstandard group, the first
task is to determine exactly which parameters are already known,
and which will need to be developed from scratch. In this case,
only the atoms forming the connection between the ligand glutamine
and CYS84 are likely to contain unknown parameters, as this
connection is special to the reaction mechanism of hisH.
In order to assign initial values to the missing Charmm22
parameters, we will use the program MOE. These values will be
checked and redefined using semi-empirical calculations will be
performed with the quantum chemistry package Spartan. Finally we
will incorporate the newly created parameters into a preexisting
Charmm22 parameter file so that we can perform a minimization of
hisH with NAMD2.
When developing the new parameters for this nonstandard residue,
we will neglect any solvent effects and consider the molecule to
be in the gas phase. The glutamine-cysteine linkage is defined as
a new residue in the Charmm22 topology file with the name CYG. We
will parameterize a truncated form of CYG in order to simulate
step III. The truncated CYG has the following formula:
CH3-S-CO-CH3 and its IUPAC name is methyl thioethanoate.
Below is the final topology file entry for the CYG residue. This
exercise will show you how to develop the values appearing in it.
RESI CYG 0.00
GROUP
ATOM N NH1 -0.47 ! |
ATOM HN H 0.31 ! HN-N
ATOM CA CT1 0.07 ! | HB1
ATOM HA HB 0.09 ! | |
GROUP ! HA-CA--CB--SG
ATOM CB CT2 -0.11 ! | | |
ATOM HB1 HA 0.09 ! | HB2 |
ATOM HB2 HA 0.09 ! O=C |
ATOM SG S -0.07 ! | \
!ATOM HG1 HS 0.16 ! \
GROUP ! \
ATOM CDG CC 0.55 ! \
ATOM OE1 O -0.55 ! \
GROUP ! HN2G \
ATOM CGG CT2 -0.18 ! | \
ATOM HG1G HA 0.09 ! HN1G-NG HB1G HG1G\
ATOM HG2G HA 0.09 ! | | | \
GROUP ! HAG-CAG--CBG--CGG--CDG=OE1
ATOM CBG CT2 -0.18 ! | | |
ATOM HB1G HA 0.09 ! | HB2G HG2G
ATOM HB2G HA 0.09 ! O1G=CG
GROUP ! |
ATOM CG CD 0.75 ! O2G-HO2G
ATOM O1G OB -0.55
ATOM O2G OH1 -0.61
ATOM HO2G H 0.44
ATOM CAG CT1 -0.12
ATOM HAG HB 0.09
ATOM NG NH3 -0.62
ATOM HN1G HC 0.31
ATOM HN2G HC 0.31
GROUP
ATOM C C 0.51
ATOM O O -0.51
BOND CB CA SG CB N HN N CA
BOND C CA C +N CA HA CB HB1
BOND CB HB2
BOND SG CDG CDG CGG CGG HG1G CGG HG2G
BOND CGG CBG CBG HB1G CBG HB2G
BOND CBG CAG CAG HAG CAG NG CAG CG
BOND NG HN1G NG HN2G CG O2G O2G HO2G
DOUBLE O C CDG OE1 CG O1G
IMPR N -C CA HN C CA +N O
IMPR CDG OE1 SG CGG CG O1G O2G CAG
DONOR HN N
DONOR HN2G NG HN1G NG HO2G O2G
ACCEPTOR O C OE1G CDG O1G CG O2G CG NG CAG
Note the following features in the Charmm22 topology file:
- In the second column you can find the atom name of each individual atom. The connectivity of the atoms is depicted in the drawing.
- In the third column the atom type is designated for each atom. The parameter files of force fields have not chemical properties for individual atoms of the system. They have parameters only for atom types in order to minimize the number of entries in the file. It is assumed that the chemical properties of i.e. every carbonyl group are the same and are independent from the individual atom properties. From this column the force field extracts the information for assigning the right parameters during the simulation. If you want to distinguish two chemical functional groups from each other you have to give them different atom types in the force field. Assigning only different atom names is not sufficient.
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width...
... torsional terms be the same
for both functional groups? }
\end{minipage}
}](img30.gif)
- The fourth column shows the partial charge of each atom. There are various quantum mechanical methods available for assigning partial charges in force fields. We will calculate partial charges from the electrostatic potential (ESP charges). The atoms are grouped in sets, which the net charge of each set is zero. This allows simulations of large residues when an electrostatic cutoff is applied as every group is a separate entity.
- On the bottom you can find Bond and Improper (IMPR) entries. These entries define the connectivity and the planarity of residues. Angles are autogenerated in Charmm22.
Below is an excerpt from a Charmm22 parameter file that
shows some required parameters necessary for a minimization run.
The force field below contains the final missing heavy atom
parameters for CYG and can be used as a reference for the
assessment of the parameters you develop in the next few
exercises. Due to time constraints, for the following exercises,
we will only perform semi-empirical calculations. The final
parameter set was developed using a higher level of theory (an ab
initio Hartree-Fock calculation with the 6-31G** basis set).
Therefore the final parameter values presented below may differ
slightly than the ones you determine.
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width...
...tane
(both systems have the same number of heavy atoms)? }
\end{minipage}
}](img31.gif)
BONDS
!
!V(bond) = Kb(b - b0)**2
!
!Kb: kcal/mole/A**2
!b0: A
!
!atom type Kb b0
! Modified for CYG residue after 6-31G** geometry optimization Felix
S CC 240.000 1.7814 ! ALLOW ALI SUL ION
ANGLES
!
!V(angle) = Ktheta(Theta - Theta0)**2
!
!V(Urey-Bradley) = Kub(S - S0)**2
!
!Ktheta: kcal/mole/rad**2
!Theta0: degrees
!Kub: kcal/mole/A**2 (Urey-Bradley)
!S0: A
!
!atom types Ktheta Theta0 Kub S0
!
! Modified for CYG residue after 6-31G** geometry optimization
CT2 S CC 34.000 100.2000 ! ALLOW ALI SUL ION
CT2 CC S 50.000 114.5000 ! ALLOW ALI SUL ION
O CC S 75.000 122.2000 ! ALLOW ALI SUL ION
Note the following features in the Charmm22 parameter
file:
- It contains all numerical values required for Charmm22 energy functions
explained in section 2 of this tutorial. The forcefield contains
entries for bonds, angles, dihedrals, impropers and nonbonded
interactions. The forcefield also contains comments describing
where these values have been obtained either by experimental
spectroscopic measurements or quantum mechanical calculations.
- The bond and angle entries contain the value for the force constant
in the first column in the physical units of kcal/mole/Å. The
second column contains equilibrium bond or angle distance in Å
or degrees, respectively.
- The next section contains the torsion angles comprised of dihedrals and
impropers. The individual values will be explained in the course
of the exercise and you will perform a dihedral drive of the
torsion CT3-S-CC-CT3.
The values for the nonbonded interactions are the standard
VDW parameters in Charmm22 required for the Lennard-Jones
potential of your atom types.
We will begin parameterizing CYG in this exercise. First
you have to build the truncated CYG residue. MOE will use pattern
recognition on the Charmm22 force field and the atom types to
assign initial values to any unknown parameters. Afterwards, we
will set up a minimization run with our newly developed parameters
and calculate one dihedral rotational barrier in the truncated
CYG.
Open the Builder in the right column.
MOE has pre-defined templates for many functional groups. Here, we
are going to build a chain of C-S-CO-C (hydrogens will be added
automatically). In the Molecule Builder:
Click on C
Now to add the next atom, click on the very end of one of the hydrogens. When you click with the left mouse button
on a hydrogen, a pink arrowhead will appear indicating that it is selected.
Click on S
Repeat this sequence, making sure to select a hydrogen on the previous group is selected before adding a new
group
Click on Close to exit the builder and deselect all atoms by clicking
on empty space in the MOE window. Change the rendering style to ball and
stick by:
Render: Ball and Stick
Experiment with different rendering styles. An example of ball and
stick is shown in Figure 4.
Figure 4:
The truncated residue CYG, as it appears in
MOE.
![\begin{figure}
\begin{center}
\latex{
\includegraphics[scale=0.5]{FIGS/moe_mole}
}
\end{center}
\end{figure}](img32.gif) |
Now it is time to specify the force field and options we want to
use for our calculations. As mentioned previously, we will perform
our calculations in gas phase, i.e., no explicit or implicit
solvation models. The dielectric constant used for electrostatic
interactions will be set to one with no distance-dependency.
Compute: Mechanics: Potential Control
Make sure that the loaded force field is charmm22.ff and click Close.
Next, display the atom types and partial charges of the atoms.
Label: MM Type
Label: Charges
You will notice a charge of zero on each atom because we have not loaded
in the Charmm22 force field. The atom types are displayed together with
the partial charges. Note that the atom types for the terminal methyl
groups (CT3) are different from the oxygen bound carbon atom (C). They
correspond to carbon atoms that are electronically different. Note also
that all hydrogen atoms have the same atom type (HA). All the hydrogens
are electronically equivalent, since all are bonded to sp3 carbons.
Figure 5:
What your potential setup box should look
like.
![\begin{figure}
\begin{center}
\latex{
\includegraphics[scale=0.5]{FIGS/potential}
}
\end{center}
\end{figure}](img33.gif) |
The partial charges of all the atoms need to be "assigned." In order to do this, click on:
Compute: Partial Charges: Force Field Charges
The charges are now defined according to the Charmm22 force field
for the corresponding atoms. Note that all equivalent hydrogens
have the same charge, and that the total charge of CYG sums to
zero as expected (you can do this by selecting Label: Charge.
You can look at the parameters for the truncated CYG molecule by clicking Commands in the
righthand column and then clicking:
Compute: Mechanics: Parameter Report
Browse through the window to look at the parameters. The parameters are copied below. Additional descriptions of the force
field can be found under the HELP menu in the main window.
loading force field '$MOE/lib/charmm22.ff'
E str ang stb tor oop ele vdw
sol
ALL: 216.023 185.641 2.489 0.000 8.629 0.000 0.000 19.263
0.000
loading forcefield '$MOE/lib/charmm22.ff'
FORCE FIELD PARAMETERIZATION SUMMARY
Mon May 12 19:47:45 2003
The following sections summarize the force field parameters used
for bond stretch, angle bending, proper and improper torsions. Van
der Waals and hydrogen bond parameters are not listed.
ATOM SUMMARY
All atoms relevant to the summary are listed below. Each atom is
listed on a separate line that contains its name, element symbol,
ionization, hybridization, partial charge, mass (amu), radius,
and its potential type. If the potential type is not known, then
the line is marked a >.
Chain 1: <noname>
Residue 1: * 0 none
1: CT3 C +0 sp3 q=-0.220 m=12.0110 r=2.06 MM=CT3
2: S S +0 sp3 q=-0.057 m=32.0660 r=2.00 MM=S
3: HA H +0 sp q= 0.090 m= 1.0080 r=1.32 MM=HA
4: HA H +0 sp q= 0.090 m= 1.0080 r=1.32 MM=HA
5: HA H +0 sp q= 0.090 m= 1.0080 r=1.32 MM=HA
6: C C +0 sp2 q= 0.517 m=12.0110 r=2.00 MM=C
7: CT3 C +0 sp3 q=-0.270 m=12.0110 r=2.06 MM=CT3
8: HA H +0 sp q= 0.090 m= 1.0080 r=1.32 MM=HA
9: HA H +0 sp q= 0.090 m= 1.0080 r=1.32 MM=HA
10: HA H +0 sp q= 0.090 m= 1.0080 r=1.32 MM=HA
11: O O +0 sp2 q=-0.510 m=15.9990 r=1.70 MM=O
BOND STRETCH (1-2) PARAMETERIZATION SUMMARY
Each bond stretch interaction is listed below. For each
interaction, the atom numbers and atom names of the atoms involved
are printed along with the equilibrium bond length (A) and the
quartic force constants (kcal/mol/A**i).
A1 A2 N1 N2 len k2 k3 k4
---- ---- ---- ---- ----- -------- -------- --------
1 5 CT3 HA 1.111 322.000 0.000 0.000
1 2 CT3 S 1.816 240.000 0.000 0.000
> 2 6 S C 1.732 264.210 -528.420 616.490
3 1 HA CT3 1.111 322.000 0.000 0.000
4 1 HA CT3 1.111 322.000 0.000 0.000
7 10 CT3 HA 1.111 322.000 0.000 0.000
7 9 CT3 HA 1.111 322.000 0.000 0.000
7 6 CT3 C 1.490 250.000 0.000 0.000
8 7 HA CT3 1.111 322.000 0.000 0.000
11 6 O C 1.230 620.000 0.000 0.000
ANGLE BEND (1-3) PARAMETERIZATION SUMMARY
Each bond angle interaction is listed below. For each interaction,
the atom numbers and atom names of the atoms involved are printed
along with the equilibrium bond angle (deg) and the quartic force
constants (kcal/mol/deg**i).
A1 A2 A3 N1 N2 N3 ang k2 k3 k4
---- ---- ---- ---- ---- ---- ----- ------- ------- -------
5 1 2 HA CT3 S 111.3 46.100 0.000 0.000
4 1 5 HA CT3 HA 108.4 35.500 0.000 0.000
4 1 3 HA CT3 HA 108.4 35.500 0.000 0.000
4 1 2 HA CT3 S 111.3 46.100 0.000 0.000
3 1 5 HA CT3 HA 108.4 35.500 0.000 0.000
3 1 2 HA CT3 S 111.3 46.100 0.000 0.000
> 1 2 6 CT3 S C 120.0 63.449 -25.447 0.000
7 6 11 CT3 C O 121.0 80.000 0.000 0.000
> 7 6 2 CT3 C S 120.0 66.643 -26.728 0.000
> 11 6 2 O C S 120.0 83.697 -33.568 0.000
10 7 9 HA CT3 HA 108.4 35.500 0.000 0.000
10 7 6 HA CT3 C 109.5 33.000 0.000 0.000
9 7 6 HA CT3 C 109.5 33.000 0.000 0.000
8 7 10 HA CT3 HA 108.4 35.500 0.000 0.000
8 7 9 HA CT3 HA 108.4 35.500 0.000 0.000
8 7 6 HA CT3 C 109.5 33.000 0.000 0.000
TORSION (1-4) PARAMETERIZATION SUMMARY
Each torsion involving 4 atoms bonded in a sequence is listed
once.
A1 A2 A3 A4 N1 N2 N3 N4 v1 v2 v3 v4 v5
---- ---- ---- ---- ---- ---- ---- ---- ------ ------- ------ ------ ------
> 5 1 2 6 HA CT3 S C 0.000 0.000 0.000 0.000 0.000
> 4 1 2 6 HA CT3 S C 0.000 0.000 0.000 0.000 0.000
> 3 1 2 6 HA CT3 S C 0.000 0.000 0.000 0.000 0.000
> 1 2 6 7 CT3 S C CT3 0.000 -2.372 0.000 0.000 0.000
> 1 2 6 11 CT3 S C O 0.000 -2.372 0.000 0.000 0.000
10 7 6 11 HA CT3 C O 0.000 0.000 0.000 0.000 0.000
> 10 7 6 2 HA CT3 C S 0.000 0.000 0.000 0.000 0.000
9 7 6 11 HA CT3 C O 0.000 0.000 0.000 0.000 0.000
> 9 7 6 2 HA CT3 C S 0.000 0.000 0.000 0.000 0.000
8 7 6 11 HA CT3 C O 0.000 0.000 0.000 0.000 0.000
> 8 7 6 2 HA CT3 C S 0.000 0.000 0.000 0.000 0.000
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width...
...d we be calculating with a quantum chemistry
calculation?}
\end{minipage}
}](img34.gif)
Note the dihedral (torsional) parameters. The analytical form of a dihedral term in the CHARMM force field:
![\begin{displaymath}
V_\phi = k_\phi \left[ 1+ \left( \cos \left(n\phi-\delta\right)\right)\right]
\end{displaymath}](img35.gif) |
(2) |
where 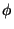 is the value of the dihedral angle,
is the value of the dihedral angle, 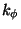 is the
force constant, n is the symmetry of the rotor (e.g. 3 for methyl
groups) and
is the
force constant, n is the symmetry of the rotor (e.g. 3 for methyl
groups) and 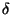 is the phase. MOE follows this analytical
form, but lists the parameters in a different format: The first
four numbers are the atom numbers in the molecule. The four atom
types are the atom types for which a torsional term is defined and
will be calculated. Then follow five numerical values. These
values correspond to the
is the phase. MOE follows this analytical
form, but lists the parameters in a different format: The first
four numbers are the atom numbers in the molecule. The four atom
types are the atom types for which a torsional term is defined and
will be calculated. Then follow five numerical values. These
values correspond to the 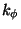 constant of the analytical form
given above. Each of the five terms correspond to n = 1 to 5 in
the analytical function given above, i.e., up to five values of n
can be used simultaneously, each with a different force constant.
The n = 1 term, with a positive
constant of the analytical form
given above. Each of the five terms correspond to n = 1 to 5 in
the analytical function given above, i.e., up to five values of n
can be used simultaneously, each with a different force constant.
The n = 1 term, with a positive 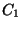 constant, has a single
minimum at 180 degrees or the trans conformation. A negative value
of
constant, has a single
minimum at 180 degrees or the trans conformation. A negative value
of 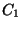 will create a maximum at 180 degrees, and therefore
create a minimum at the cis conformation. The n = 2 term, with a
positive
will create a maximum at 180 degrees, and therefore
create a minimum at the cis conformation. The n = 2 term, with a
positive 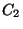 value, creates minima at 90 and 270 degrees. A
negative
value, creates minima at 90 and 270 degrees. A
negative 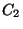 value creates minima at 0 and 180 degrees, which is
useful for enforcing planarity. The n = 3 term, with a positive
value creates minima at 0 and 180 degrees, which is
useful for enforcing planarity. The n = 3 term, with a positive
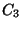 , creates maxima at 0, 120 and 240 degrees, which will
emphasize the staggered conformation of sp3 carbons. A negative
, creates maxima at 0, 120 and 240 degrees, which will
emphasize the staggered conformation of sp3 carbons. A negative
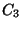 will emphasize the eclipsed conformation.
For instance, the line:
will emphasize the eclipsed conformation.
For instance, the line:
9 8 5 1 HA CT2 CT2 CT3 0.000 0.000 0.195 0.000 0.000
could also be written, for these four atoms:
![\begin{displaymath}
V_\phi = 0.195\cdot\left[1+\cos\left(3\phi\right)\right]
\end{displaymath}](img39.gif) |
(3) |
Since we only have a force constant for n=3, the value of the
force constant is 0.195, and the phase is zero (d = 0 since we
have +0.195 and not 0.195). A sample Matlab plot of this function
is presented below. In standard CHARMM notation, the exact same
information would be written as follows:
HA CT2 CT2 CT3 3 0.195 0
i.e., the four atom types, the symmetry of the rotor (n), the force constant (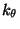 ) and the phase (d).
Be sure to save your generated CYG molecule for later reference:
) and the phase (d).
Be sure to save your generated CYG molecule for later reference:
File: Save as: File format PDB
Figure 6:
Matlab plot of Eq. (3) presented
above.
![\begin{figure}
\begin{center}
\latex{
\includegraphics[scale=0.5]{FIGS/dihedral}
}
\end{center}
\end{figure}](img40.gif) |


Next: Semi-empirical parameter generation: SPARTAN
Up: VMD Tutorial
Previous: The CHARMM22 Force Field
vmd@ks.uiuc.edu
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width...
... torsional terms be the same
for both functional groups? }
\end{minipage}
}](img30.gif)
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width...
... torsional terms be the same
for both functional groups? }
\end{minipage}
}](img30.gif)
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width...
...tane
(both systems have the same number of heavy atoms)? }
\end{minipage}
}](img31.gif)
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width...
...d we be calculating with a quantum chemistry
calculation?}
\end{minipage}
}](img34.gif)