Proton transfer reactions are of great importance
in chemistry and in biomolecular processes of living organisms.
The latter include most enzymatically catalyzed reactions, e.g.
ATP hydrolysis/synthesis by
F1F0-ATPsynthase.
Furthermore, the protonation state of chemical groups, e.g.
the side chains of amino acids, is fundamentally related to their
biomolecular function. The deprotonation/protonation of a given chemical
group can be represented schematically as
.
A measure of the probability of a chemical group to be
protonated/unprotonated is given by the pKa defined via
.
The pKa of a protonable group strongly depends on
its molecular environment. It is possible to measure the pKa
experimentally, but this is generally not an easy task.
In a gas phase environment there are two quantities which are used to describe the ability of a molecule to accept a proton. The first one is the gas phase basicity and is the negative of the free energy associated with the protonation/deprotonation reaction. A second and more frequently used quantity is the proton affinity P(A), defined as the negative of the enthalphy change at standard condition (i.e. temperature and pressure). Computational ab initio approaches can provide reliable values for proton affinities, which is important since they are hard to determine experimentally. In the following you will determine the proton affinity of water and its dependence on the level of theory employed to perform the calculation (i.e. basis set, electron correlation). Using your experience with water, you will then be able to estimate the proton affinity of methanol, CH3OH.
The proton affinity for the reaction
is defined as the negative of the reaction
enthalpy at 298.15K, and hence (T: temperature, R: ideal gas constant)
The energy of a nonlinear polyatomic molecule can be approximated as
Here ZPE stands for the zero point energy of the normal modes. From statistical mechanics we know that the contributions Erot and Etrans both equal 3/2 RT. Furthermore, E’vib can usually be neglected compared to the zero point energy ZPE. To determine the proton affinity one has to calculate the energy change in going from the reactant A- and H+ to the product AH. The rotational energy contribution remains constant (since the proton does not posses rotational kinetic energy) and the translational energy of the proton contributes -3/2 RT. Hence, neglecting the contribution due to the vibrations as argued above, one obtains the following expression for the proton affinity
To determine the proton affinity one therefore has to calculate two contributions: the change in electronic energy given by (note that the contribution of the proton is zero)
and the difference in zero point energies. In order to calculate the energies of AH and A- you have to first optimize both systems. The ZPE can then be obtained by calculating the normal modes of the system via determination of the Hessian matrix.
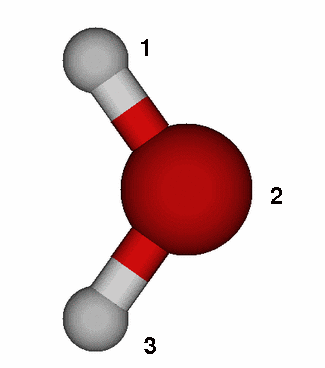
You will start with a very simple, but important,
test system and determine
the proton affinity of water. During the first calculation you will employ
Hartree-Fock theory and the 6-31G basis set.
In the case of water one can schematically
write 
The unprotonated/protonated species correspond to H2O and
H3O+ respectively. You therefore have to minimize
both H2O and H3O+ and subsequently determine
the electronic and the zero point energy at the minimum conformation.
First go into the working directory for part 2, and then into the directory for the proton affinity of water, i.e. QM_tutorial/part2/pa_wat. Please run the minmization of H2O and H3O+ in the directories wat631 and h3o631 respectively. After what you learned during the first part of the hands-on session you are now ready to set up the minimization runs yourself. You can use the input files for the minimization run of part 1 (the retinal analogue) as template and change the $DATA group as well as the number of internal coordinates in NZVAR. In order to construct the initial Z-matrix you may assume an O-H bond length of 0.95Å, a bond angle of 109 degrees and a dihedral of 120 degrees in the case of H3O+. It is useful if you make a schematic drawing of both molecules and use them to identify the internal coordinates. You can use the figure on the right as template. Please also add the keyword HSSEND=.TRUE. to the $STATPT group to enforce evaluation of the Hessian matrix during the same computation, after the geometry search has converged. If you need help you can consider the sample files in the sample_files directory but we urge you to try it yourself and consider the GAMESS manual for help.
After you have completed setting up the two runs start your jobs using the rungms script. As a reminder how to go about doing that, type
tbss> rungms [inputfile] >& [outputfile]
They should both complete quickly and once they are finished make sure that they both terminated normally and the geometry optimization actually converged. Extract the final energies, which are output in the log files in the following form (you need the TOTAL ENERGY)
-----------------
ENERGY COMPONENTS
-----------------
WAVEFUNCTION NORMALIZATION = 1.0000000000
ONE ELECTRON ENERGY = -730.8096432790
TWO ELECTRON ENERGY = 277.7469135169
NUCLEAR REPULSION ENERGY = 204.9489137980
------------------
TOTAL ENERGY = -248.1138159640
ELECTRON-ELECTRON POTENTIAL ENERGY = 277.7469135169
NUCLEUS-ELECTRON POTENTIAL ENERGY = -979.1237023677
NUCLEUS-NUCLEUS POTENTIAL ENERGY = 204.9489137980
------------------
TOTAL POTENTIAL ENERGY = -496.4278750527
TOTAL KINETIC ENERGY = 248.3140590887
VIRIAL RATIO (V/T) = 1.9991935893
Next, extract the zero point energies (look for HARMONIC ZERO POINT ENERGY and pick the kcal/mol value) which you can find at the bottom of the log file and which should look similar to
-------------------------------
THERMOCHEMISTRY AT T= 298.15 K
-------------------------------
USING IDEAL GAS, RIGID ROTOR, HARMONIC NORMAL MODE APPROXIMATIONS.
P= 1.01325E+05 PASCAL.
ALL FREQUENCIES ARE SCALED BY 1.00000
THE MOMENTS OF INERTIA ARE (IN AMU*BOHR**2)
5.00304 5.00307 10.00611
THE ROTATIONAL SYMMETRY NUMBER IS 1.0
THE ROTATIONAL CONSTANTS ARE (IN GHZ)
360.39877 360.39646 180.19881
THE HARMONIC ZERO POINT ENERGY IS (SCALED BY 1.000)
0.036419 HARTREE/MOLECULE 7993.049924 CM**-1/MOLECULE
22.853299 KCAL/MOL 95.618205 KJ/MOL
Using these values you can then
calculate the proton affinity of water obtained via HF/6-31G
(use T=298K and R=1.9872 cal mol-1 K-1).
First you need to determine
and
Note that since the energy difference
is in Hartree (this is what GAMESS provides you with in the output file)
you have to convert it to kcal/mol by multiplying it with a factor of 627.53
(1 Hartree = 627.53 kcal/mol). The difference in zero point energy
already is in kcal/mol (since this is the value you picked from the log
file). Finally, from the equation
you can now calculate the proton affinity for water at an HF/6-31G level of theory.
Now that we have calculated the proton affinity using a rather "small" basis set, we need to find out the effect of a larger basis on the value of the proton affinity. In order to be able to estimate this you will next perform a similar calculation (i.e. use the same initial structure) employing a large basis set, namely the TZV triple zeta basis with additional polarization and diffuse functions. You can select this basis by changing your $BASIS group to $BASIS GBASIS=TZV NDFUNC=1 NPFUNC=1 DIFFSP=.TRUE. DIFFS=.TRUE. $END. Using this basis set, perform minimizations and Hessian matrix calculations of H2O and H3O+. Please use the directories wattzv and h3otzv for this purpose and consider the sample_files if you need help. Use this to obtain a second value for the proton affinity P(H2O) (i.e. calculate it!).
Don’t forget to use MOLDEN to look at your system. Compare the final minimized structure with the one obtained using HF/6-31G, particularly the one of H3O+. You will observe that the HF/6-31 level of theory is not able to yield the correct non-planar structure of H3O+.
Next you will examine the effect of electron correlation on the calculated value of the proton affinity. You will use the HF/6-31G basis and the coupled cluster methodology with single and double excitations and triples-correction (CCSD(T)) to account for electronic correlation. Since the CCSD(T) method only allows single point energy calculations and no optimizations, you have to calculate the CCSD(T) energy at the final HF/6-31G minimized conformation. Please perform the calculations for H2O and H3O+ in the directories wat631cc and h3o631cc. For each H2O and H3O+ start from your 6-31G input files (this is the first calculation we did), replace the initial coordinates with the optimized ones (from 6-31G) and insert the keyword CCTYP=CCSD(T) in the $CONTRL group to request a CCSD(T) calculation. Don’t forget to change RUNTYP to RUNTYP=ENERGY since we are only performing a single point run and remove HSSEND=.TRUE. in the $STATPT group.
For simplicity you may assume that the ZPE for the CCSD(T) calculation is the same as for the initial HF/6-31G run, although this is, of course, an over-simplification. If you are not sure that your files are correct you may peek at the CCSD(T) input file in the sample_file directory. After your simulations have terminated successfully, extract the energies to calculate the proton affinity P(H2O) at the CCSD(T)//HF/6-31G level of theory.
Finally, you will calculate the proton affinity of water using the highest and most sophisticated level of theory available (at least in GAMESS), namely CCSD(T) with the TZV basis set. You should use the TZV minimized structure as input for the CCSD(T) single point energy evaluation as described in the previous paragraph. This will provide the fourth and most refined value for P(H2O). Please perform this calculations in the directories h3o631cc and wattzvcc.
Next, compare the 4 calculated values of P(A) for the
different levels of theory you considered above, as well
as the individual contributions (i.e.
and
)
What is the effect of the size of the basis set and the correlation effects?
The experimental value of P(A) for water is P(A)=165 kcal/mol; which of
your four calculations comes closest?
For the simple case of water, it was straightforward
to calculate
and
even using a very large and
computationally expensive level of theory like CCSD(T)//HF/TZV. Such a calculation
will only be possible for the smallest systems and will become prohibitive even
for medium sized molecules. A way to approximate the proton affinity for a
larger molecule is to calculate the proton affinity at a lower level of
theory (e.g. HF/6-31G) and then add corrections which approximately account for the
basis set size and/or electron correlation. You should use the water
example to calculate corrections C1 and C2 which arise due to a different
basis set size and electron correlation effects respectively.
To obtain correction C1
simply calculate the difference in P(A) for the HF/6-31G and HF/TZV levels of
theory; similarly subtract the P(A) from HF/6-31G from CCSD(T)//HF/TZV to obtain C2.
Hence:
C1 = P(H2O,HF/TZV) - P(H2O,HF/6-31G) C2 = P(H2O,CCST(T)//HF/6-31G) - P(H2O,HF/6-31G)
You can now estimate P(H2O,CCSD(T)//HF/TZV) by adding corrections C1 and C2 to P(H2O,HF/6-31G). How well does this result agree with the value you actually calculated in the last example? Why are they different and what assumptions have been made by simply assuming additivity? You can check you results for the proton affinities P(A) and the correction factor C1 and C2 by clicking here.
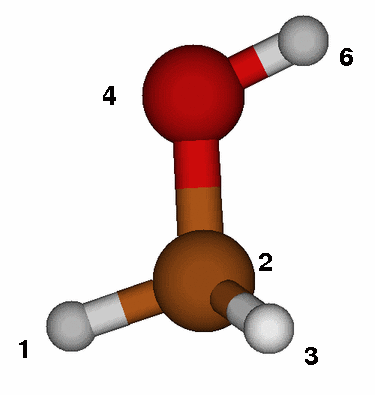
In this section you will utilize the experience
gained in calculating the proton affinity of water to estimate
P(CH3OH), the proton affinity of methanol.
All the calculations in this part will be performed in the directory
QM_tutorial/part2/pa_met hence
make sure to go there first. The water example
has shown that you should use a high level of theory, e.g.
CCSD(T)//HF/TZV to do proton affinity calculations.
Since a simulation at this level of theory for methanol would
take too long, you will have to determine P(CH3OH) at an HF/6-31G
level of theory and then use the corrections C1 and C2 determined for water to take
into account the larger basis set as well as electron correlation
(this is what we did at the end of the last part for water).
The two species you have to consider for calculating
and
are the protonated and un-protonated species, namely
CH3OH and CH3O+. Hence set up
the input files to perform an energy minimization with subsequent Hessian
matrix calculation at an HF/6-31G level of theory for both molecules.
Please perform all calculations in the directories
ch3oh631 and ch3o631.
To determine the Z-matrix you might want to sketch each molecule on a piece
of paper and determine the bonds, angles and
dihedrals you need to describe the system. You may assume that the
CH3 group has a tetrahedral conformation with a C-H bond length of
1.1Å. The C-O bond length can be estimated at 1.4Å,
the O-H bond with 0.95Å.
Please try it yourself since mastering this task is very important.
Use the figure on the left as template and employ the same atom numbering
in the Z-matrix (atom number 5 is hidden behind the carbon!).
In case you get stuck you may peek at the sample_files.
After you are done with the calculations you are ready to compute P(CH3OH) at the HF/6-31G level of theory and estimate the CCSD(T)//HF/TZV value by adding the correction C1 and C2 determined for water. We have computed the actual value of P(CH3OH) at the CCSD(T)//HF/TZV level for you and you should compare them to your estimated values. Do so by considering the pre-calculated files in ch3ohcc and ch3occ or simply by looking at the values given here.
Of great interest, particularly in a biomolecular setting is the dependence of proton affinities on the molecular environment. So far you have assumed that the proton transfer takes place in the gas phase, i.e. in vacuum, which is of course not the case in a real system. To study the influence of the environment on the proton affinity you can, e.g., embed your molecule in a solvent environment or surround it by e.g. protein residues. The first task can be accomplished inside GAMESS using the $PCM input group which allows to immerse the system in a dielectric environment modeling the influence of solvent (c.f. the GAMESS manual). You can also design or pick from an appropriate pdb file part of a protein and study e.g. the proton affinity of water inside a cavity. The overall system size should still be small, otherwise the simulations will take a long time. There are many more issues to be examined and you are encouraged to explore them yourself.