Developing Topology and Parameter Files

When presented with a nonstandard group, the first task is to determine exactly which parameters are already known, and which will need to be developed from scratch. The unparameterized part of the CYG residue is the connection between the sulfur and the carbon. The connection between the sulfur of CYS and the carbonyl carbon of the glutamine is called a thioester bond. By attaching the substrate in such a way, you have created a glutamyl thioester intermediate. In order to use this CYG residue in MD simulations, we need to make a topology file entry for it as well as develop a complete set of parameters describing it.

To do this, we will integrate two pre-existing topology/parameter file entries - a cysteine entry and glutamine entry. From a chemical and biological standpoint, this should make intuitive sense: though connected in a new way, we can still expect the two bonded residues to behave (for the most part) as they would when they are separate entities. The chemical and physical behavior of CYG should be similar to CYS and GLN.

The topology file specifies the partial charge of each atom and the connectivity of the atoms. We will then use the topology file when we create the .psf and .pdb file for our simulations. The parameter file specifies the specific equilibrium bond lengths and angles, bond and angle force constants, dihedrals, and impropers. We need bond, angle, and dihedral parameters for the atoms around this new residue, and we will generate them in the next exercise. The creation of both the topology file entry and the missing parameters are discussed in detail now.

An Introduction to a CHARMM Topology File

Below is the final topology file entry for the CYG residue. The CYG parameters appearing in it were created by combining a regular CYS entry (with the HG1 atom of CYS deleted) with a GLN entry (with the NH2 atom of GLN deleted). When merging the two residues into one, at the place where you connect the groups you will have to delete atoms (in this case a hydrogen on cysteine's S and the NH2 atom of the glutamine) and alter the charges. Following the standard CHARMM protocol, the HG1 atom on CYS was deleted and its charge was moved to SG (-0.23 + 0.16 = -0.07). In the CYG entry, you can see the line for HG1 has been commented out (comments are denoted by ! marks), and the charge added to the S. Note that the group still has an overall neutral value.

Take a few minutes and look through one of the topology files we have supplied you. To do this, at a unix prompt, type:

more top_all27_prot_lipid_prfar_cyg_cyn.inp

Look at a regular CYS and GLN residue entries, and be sure you understand how we have pasted them together to make CYG below.

RESI CYG 0.00
GROUP
ATOM N    NH1    -0.47  !     |
ATOM HN   H       0.31  !  HN-N
ATOM CA   CT1     0.07  !     |   HB1
ATOM HA   HB      0.09  !     |   |
GROUP                   !  HA-CA--CB--SG
ATOM CB   CT2    -0.11  !     |   |   |
ATOM HB1  HA      0.09  !     |   HB2 |
ATOM HB2  HA      0.09  !   O=C       |
ATOM SG   S      -0.07  !     |        \
!ATOM HG1  HS      0.16 !               \
GROUP                   !                \
ATOM CDG   CC      0.55 !                 \
ATOM OE1   O      -0.55 !                  \
GROUP                    !     HN2G         \
ATOM CGG   CT2    -0.18  !      |            \
ATOM HG1G  HA      0.09  ! HN1G-NG   HB1G HG1G\
ATOM HG2G  HA      0.09  !      |    |     |   \
GROUP                    !  HAG-CAG--CBG--CGG--CDG=OE1
ATOM CBG   CT2    -0.18  !      |    |     |
ATOM HB1G  HA      0.09  !      |    HB2G HG2G
ATOM HB2G  HA      0.09  !  O1G=CG
GROUP                    !      |
ATOM CG    CD      0.75  !      O2G-HO2G
ATOM O1G   OB     -0.55
ATOM O2G   OH1    -0.61
ATOM HO2G  H       0.44
ATOM CAG   CT1    -0.12
ATOM HAG   HB      0.09
ATOM NG    NH3     -0.62
ATOM HN1G  HC       0.31
ATOM HN2G HC      0.31
GROUP
ATOM C    C       0.51
ATOM O    O      -0.51
BOND CB CA   SG CB   N HN  N  CA
BOND C  CA   C +N  CA HA  CB HB1
BOND CB HB2
BOND SG CDG  CDG CGG CGG HG1G CGG HG2G
BOND CGG CBG CBG HB1G CBG HB2G
BOND CBG CAG CAG HAG CAG NG CAG CG
BOND NG HN1G NG HN2G CG O2G O2G HO2G
DOUBLE O  C CDG OE1  CG O1G
IMPR N -C CA HN  C CA +N O
IMPR CDG OE1 SG CGG  CG O1G O2G CAG
DONOR HN N
DONOR HN2G NG HN1G NG HO2G O2G
ACCEPTOR O C OE1G CDG O1G CG O2G CG NG CAG

Note the following features in the CHARMM27 topology file:

• In the second column you can find the atom name of each individual atom. The connectivity of the atoms is depicted in the drawing and uses the atom name. This name must match the atom name in the pdb file.
• In the third column the atom type is designated for each atom. The parameter files of force fields do not have chemical properties for individual atoms of the system. Instead, they have parameters for atom types in order to minimize the number of entries in the file. It is assumed that the chemical properties of similar atoms are the same, i.e. every carbonyl group of the backbone has similar chemical and physical properties. From this column the force field extracts the information for assigning the right parameters during the simulation. If you want to distinguish two chemically functional groups from each other, then you have to give them different atom types in the force field. Assigning only different atom names is not sufficient.

• The fourth column shows the partial charge of each atom. There are various quantum mechanical methods available for assigning partial charges in force fields. We will discuss the determination of partial charges in more detail later. The atoms are divided into groups; with the exception of charged residues (such as arginine or glutamate), the net charge of each group is neutral.

• At the end of the entry, you will find Bond (BOND)and Improper (IMPR) entries. These entries define the connectivity and the planarity of residues.

You may have noticed that although the bonds and atoms are defined in the topology file, the entry is missing angle and dihedral assignments. The angle and dihedrals are never assigned in the topology file. PSFGEN automatically determines the angles and dihedrals based on the connectivity of the atoms. This should make sense - every 3 connected atoms generates an angle and every 4 generates a dihedral term. By automatically generating the terms, PSFGEN saves you a lot of work!

An Introduction to a CHARMM Parameter File

Below is an excerpt from a CHARMM27 parameter file that shows some required (and previously missing!) parameters necessary for MD simulations. The force field excerpts below contain the final missing heavy atom parameters for CYG and can be used as a reference for the assessment of the parameters you develop in the next few exercises. Due to time constraints, for the following exercises, we will only perform semi-empirical calculations. The final parameter set was developed using a higher level of theory (an ab initio Hartree-Fock calculation with the 6-31G* basis set). Therefore the final parameter values presented below may differ slightly than the ones you determine.

BONDS
!
!V(bond) = Kb(b - b0)**2
!
!Kb: kcal/mole/A**2
!b0: A
!
!atom type Kb          b0
! Modified for CYG residue after 6-31G* geometry optimization 
S    CC   240.000      1.7814 ! ALLOW   ALI SUL ION

ANGLES
!
!V(angle) = Ktheta(Theta - Theta0)**2
!
!V(Urey-Bradley) = Kub(S - S0)**2
!
!Ktheta: kcal/mole/rad**2
!Theta0: degrees
!Kub: kcal/mole/A**2 (Urey-Bradley)
!S0: A
!
!atom types     Ktheta    Theta0   Kub     S0
!

! Modified for CYG residue after 6-31G* geometry optimization
 CT2 S    CC    34.000    100.2000 ! ALLOW   ALI SUL ION

 CT2  CC   S     50.000    114.5000 ! ALLOW   ALI SUL ION

 O    CC   S     75.000    122.2000 ! ALLOW   ALI SUL ION

DIHEDRALS
!
!V(dihedral) = Kchi(1 + cos(n(chi) - delta)) 
!
!Kchi: kcal/mole
!n: multiplicity
!delta: degrees
!
!atom types             Kchi    n   delta

CC  S    CT2  CT1      0.2400  1   180.00
CC  S    CT2  CT1      0.3700  3     0.00 
HA   CT2  S    CC      0.2800  3     0.00 
CT2   S   CC  CT2      2.05    2     180.00 
CT2   S   CC  O        2.05    2     180.00

Note the following features in the CHARMM27 parameter file:

• It contains all numerical values required for CHARMM27 energy functions explained in section 2 of this tutorial. The force field contains entries for bonds, angles, dihedrals, impropers and nonbonded interactions. The force field also contains comments describing where these values have been obtained either by experimental spectroscopic measurements or quantum mechanical calculations.
• The bond and angle entries contain the value for the force constant in the first column in the physical units of kcal/mole/Å. The second column contains equilibrium bond or angle distance in Å or degrees, respectively.
• The next section contains the torsion (a.k.a. dihedral) angles. The individual values will be explained in the course of the exercise and you will perform a dihedral drive of the dihedral HA CT2 S CC.

The values for the nonbonded interactions are the standard VDW parameters in CHARMM27 required for the Lennard-Jones potential of your atom types.

Assigning Initial Values for Unknown Parameters

Before we get into the details of parameterizing, it is useful and often very helpful to be aware of programs that are able to assist you in the process. CHARMm, AMBER, and MOE are all programs with modules that will identify which atoms are missing parameters and even give you an initial first guess of values. These programs almost always use a pattern recognition algorithm to guess for you, and any parameters they supply you will have to be checked with your chemical intuition and at least a basic level of quantum mechanics. If you choose to use one of these packaged programs, caveat emptor! While it seems like an easy solution to a sometimes difficult and always tedious process, it rarely, if ever, provides you with a suitable and/or reliable set of parameters.

A Closer Look at Dihedral Parameters

Note the dihedral (torsional) parameters. The analytical form of a dihedral term in the CHARMM force field uses cosine functions:

$$V_\phi = k_\phi \left[ 1+ \left( \cos \left(n\phi-\delta\right)\right)\right]$$ (2)

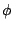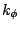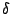where $\phi$ is the value of the dihedral angle, $k_\phi$ is the force constant, n is the symmetry of the rotor (e.g. 3 for methyl groups) and $\delta$ is the phase. In the CHARMM energy function, you can specify multiple dihedrals for the same bond. Often one needs to use multiple dihedrals in order to generate energetic barriers of proper height and location.

You can use the following table to help you generate the correct dihedrals in CHARMM.

Dihedral Parameters in CHARMM format
Multiplicity, n	Phase 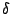$\delta$	Location of Minima	Useful Notes
1	0	180	yields trans conformation
1	180	0	yields cis conformation
2	0	90, 270
2	180	0, 180	useful for enforcing planarity
3	0	60, 180, 300	emphasizes staggered conformation of sp3 carbons
3	180	0, 120, 240	emphasizes eclipsed conformations of sp3 carbons

For instance, the line:

           HA   CT2  CT2  CT3       3         0.195         0

could also be written, for these four atoms:

$$V_\phi = 0.195\cdot\left[1+\cos\left(3\phi\right)\right]$$ (3)

i.e., the four atom types, the symmetry of the rotor (n), the force constant (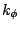$k_\phi$) and the phase (d). Since we only have a force constant for n=3, the value of the force constant is 0.195, and the phase is zero. A sample Matlab plot is shown in Fig. 4.

Figure 4: Matlab plot of Eq. (3) presented above.