

Next: Developing Topology and Parameter
Up: Parameterization Tutorial
Previous: Testing out your new
There are several versions of the CHARMM force field available from the MacKerrell website. Don't let
this confuse you! Most commonly you will see CHARMM19, CHARMM22, or CHARMM27. CHARMM22 (released
in 1991) and CHARMM27 (released in 1999) are the most recent versions of the force field. For purely
protein systems, the two are equivalent. However, if you are simulating any nucleic acids, be aware that
CHARMM27 has been optimized for simulating DNA and should be used.
The form of the potential energy function we will use in this exercise is taken directly from CHARMM22 and given by the following equation [1]:
The first term in the energy function accounts for the bond stretches
where 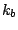 is the bond force constant and
is the bond force constant and 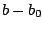 is the distance from
equilibrium that the atom has moved. The second term in the equation
accounts for the bond angles where
is the distance from
equilibrium that the atom has moved. The second term in the equation
accounts for the bond angles where 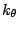 is the angle force constant
and
is the angle force constant
and
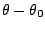 is the angle from equilibrium between 3 bonded
atoms. The third term is for the dihedrals (a.k.a. torsion angles)
where
is the angle from equilibrium between 3 bonded
atoms. The third term is for the dihedrals (a.k.a. torsion angles)
where 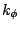 is the dihedral force constant,
is the dihedral force constant, 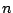 is the multiplicity
of the function,
is the multiplicity
of the function, 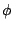 is the dihedral angle and
is the dihedral angle and 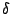 is the phase
shift. The fourth term accounts for the impropers, that is out of plane
bending, where
is the phase
shift. The fourth term accounts for the impropers, that is out of plane
bending, where 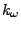 is the force constant and
is the force constant and
 is the out of plane angle. The Urey-Bradley component (cross-term
accounting for angle bending using 1,3 nonbonded interactions) comprises
the fifth term, where
is the out of plane angle. The Urey-Bradley component (cross-term
accounting for angle bending using 1,3 nonbonded interactions) comprises
the fifth term, where 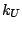 is the respective force constant and
is the respective force constant and 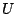 is
the distance between the 1,3 atoms in the harmonic potential. Nonbonded
interactions between pairs of atoms
is
the distance between the 1,3 atoms in the harmonic potential. Nonbonded
interactions between pairs of atoms 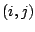 are represented by the last
two terms. By definition, the nonbonded forces are only applied to atom
pairs separated by at least three bonds. The van Der Waals (VDW) energy is calculated
with a standard 12-6 Lennard-Jones potential and the electrostatic energy
with a Coulombic potential. In the Lennard-Jones potential above, the
are represented by the last
two terms. By definition, the nonbonded forces are only applied to atom
pairs separated by at least three bonds. The van Der Waals (VDW) energy is calculated
with a standard 12-6 Lennard-Jones potential and the electrostatic energy
with a Coulombic potential. In the Lennard-Jones potential above, the
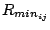 term
is not the minimum of the potential, but rather where the Lennard-Jones potential crosses
the x-axis (i.e. where the Lennard-Jones potential is zero).
In order to run the MD simulations, we need to be sure that our parameter file has all the terms specified
in the energy function we are using (i.e. the equation specified above).
term
is not the minimum of the potential, but rather where the Lennard-Jones potential crosses
the x-axis (i.e. where the Lennard-Jones potential is zero).
In order to run the MD simulations, we need to be sure that our parameter file has all the terms specified
in the energy function we are using (i.e. the equation specified above).


Next: Developing Topology and Parameter
Up: Parameterization Tutorial
Previous: Testing out your new
tutorial@ks.uiuc.edu
![$\displaystyle \sum_{\mathrm{bonds}}{k_b \left(b-b_0\right)^2} + \sum_{\mathrm{a...
...sum_{\mathrm{dihedrals}}{k_\phi \left[1+\cos\left(n\phi - \delta\right)\right]}$](img11.gif)
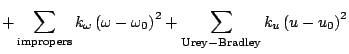
![$\displaystyle + \sum_{\mathrm{nonbonded}}{\epsilon \left[\left(\frac{R_{\mathrm...
...{R_{\mathrm{min}_{ij}}}{r_{ij}}\right)^6\right]+\frac{q_iq_j}{\epsilon r_{ij}}}$](img13.gif)
![$\displaystyle \sum_{\mathrm{bonds}}{k_b \left(b-b_0\right)^2} + \sum_{\mathrm{a...
...sum_{\mathrm{dihedrals}}{k_\phi \left[1+\cos\left(n\phi - \delta\right)\right]}$](img11.gif)
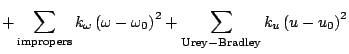
![$\displaystyle + \sum_{\mathrm{nonbonded}}{\epsilon \left[\left(\frac{R_{\mathrm...
...{R_{\mathrm{min}_{ij}}}{r_{ij}}\right)^6\right]+\frac{q_iq_j}{\epsilon r_{ij}}}$](img13.gif)
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width=2...
...ng to them? What terms are likely to dominate
the potential?
}
\end{minipage} }](img28.gif)