| (10) |
| (10) |
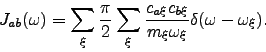 |
(12) |
The HEOM arise by assuming a form of bath correlation functions given by
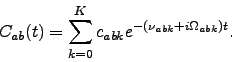 |
(13) |
| (15) |
The parameters needed to model the system are summarized in Table 1.
| Parameter | Meaning | Units |
| Number of states
|
||
| Energy level of state
|
[Energy] | |
| Interaction between states
|
[Energy] | |
| Number of system-environment coupling terms | ||
| Elements of |
||
| Strength of coupling |
[Energy] | |
| Response frequency of environment from |
[time] |
|
| Number of Matsubara terms to include | ||
| Hierarchy truncation level |