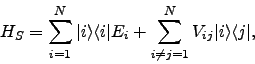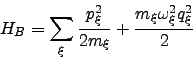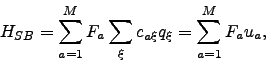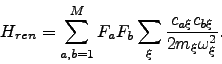


Next: Correlation functions
Up: Introduction and theory
Previous: Introduction and theory
Contents
To describe the input parameters for PHI, first the model of the quantum system has to be specified.
The quantum system is described by a total Hamiltonian
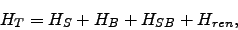 |
(1) |
where 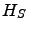 describes the system of interest,
describes the system of interest, 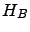 the thermal environment,
the thermal environment, 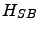 the system-environment coupling, and
the system-environment coupling, and 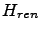 is a renormalization term (specified below) dependent on the system-environment coupling.
The system Hamiltonian describes states
is a renormalization term (specified below) dependent on the system-environment coupling.
The system Hamiltonian describes states
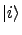 ,
, 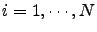 with energies
with energies 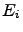 and interaction
and interaction 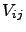 as
as
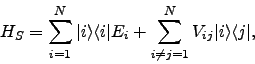 |
(2) |
The environment is modeled as an infinite set of harmonic oscillators with
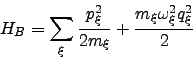 |
(3) |
The system-environment coupling is assumed to be linear given by
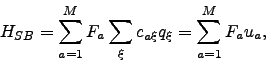 |
(4) |
where
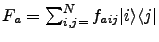 specifies the exact form of the coupling. At present only diagonal forms of
specifies the exact form of the coupling. At present only diagonal forms of 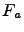 are implemented in PHI, such that
are implemented in PHI, such that
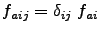 . In the present implementation only three types of
. In the present implementation only three types of 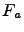 are allowed:
are allowed:
- diagonal, independent coupling:
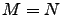 ,
,
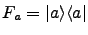
- diagonal, independent coupling:
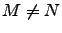 ,
,
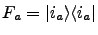 for
for
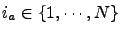 .
.
- diagonal, correlated coupling:
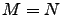 ,
,
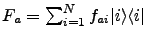
The coupling introduces a shift in the bath coordinates 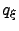 that needs to be countered with the renormalization term
that needs to be countered with the renormalization term
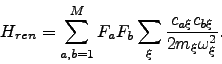 |
(5) |
Note that the renormalization term is NOT added to the system Hamiltonian in PHI - this is left up to the user to include in the Hamiltonian section of the input parameters.
PHI implements the HEOM to calculate the system density matrix 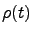 averaged over environmental fluctuations
averaged over environmental fluctuations
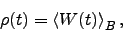 |
(6) |
where 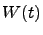 is the density matrix of the complete system + environment. The time evolution of
is the density matrix of the complete system + environment. The time evolution of 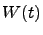 is formally calculated as
is formally calculated as
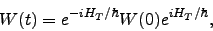 |
(7) |
Where 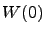 specifies the density matrix of the complete system at
specifies the density matrix of the complete system at 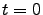 . Assuming that the environment is in thermal equilibrium and that initially the system and environment are uncorrelated, the initial density matrix is given by
. Assuming that the environment is in thermal equilibrium and that initially the system and environment are uncorrelated, the initial density matrix is given by
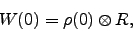 |
(8) |
where
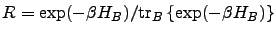 ,
, 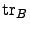 is the partial trace over bath coordinates and
is the partial trace over bath coordinates and 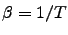 is the inverse temperature. The system density matrix evolution can be written as
is the inverse temperature. The system density matrix evolution can be written as
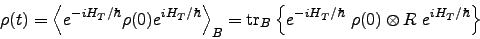 |
(9) |



Next: Correlation functions
Up: Introduction and theory
Previous: Introduction and theory
Contents
http://www.ks.uiuc.edu/Research/phi