



Next: General parameters and input/output
Up: NAMD 2.9 User's Guide
Previous: External Program Forces
Contents
Index
Collective Variable-based Calculations1
In today's molecular dynamics simulations, it is often useful to
reduce the great number of degrees of freedom of a into a few
parameters which can be either analyzed individually, or manipulated
in order to alter the dynamics in a controlled manner. These have
been called `order parameters', `collective variables', `(surrogate)
reaction coordinates', and many other terms. In this section, the
term `collective variable' (shortened to colvar) is used, and
it indicates any differentiable function of atomic Cartesian
coordinates,
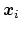 , with
, with 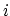 between
between 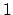 and
and 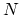 , the total
number of atoms:
, the total
number of atoms:
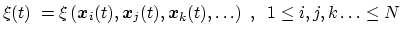 |
(35) |
The colvars module in NAMD may be used in both MD simulation and
energy minimization runs (except free energy methods).
It offers several features:
- define an arbitrary number of colvars, and perform a
multidimensional analysis or biased simulation by accessing any
subset of colvars independently from the rest (see
10.1);
- combine different functions of Cartesian coordinates (herein
termed colvar components) into a colvar defined as a
polynomial of several such components, thereby implementing new
functional forms at runtime; periodic, multidimensional and
symmetric components are handled transparently (see 10.2.2);
- calculate potentials of mean force (PMFs) for any set of
colvars, using different sampling methods: currently implemented are
the Adaptive Biasing Force (ABF) method (see
10.3.1), metadynamics (see
10.3.2), Steered Molecular Dynamics (SMD) and
Umbrella Sampling (US) via a flexible harmonic restraint bias (see
10.3.3);
- calculate statistical properties of the colvars, such as their
running averages and standard deviations, time correlation
functions, and multidimensional histograms, without the need to save
very large trajectory files.
- compute collective variable values from existing coordinates
(e.g. an MD trajectory): use NAMD's coorfile read command,
and perform a 0-timestep run for each set of coordinates, as
illustrated in 16.
Subsections




Next: General parameters and input/output
Up: NAMD 2.9 User's Guide
Previous: External Program Forces
Contents
Index
http://www.ks.uiuc.edu/Research/namd/
![]() , with
, with ![]() between
between ![]() and
and ![]() , the total
number of atoms:
, the total
number of atoms: