



Next: Introduction
Up: NAMD 2.10b1 User's Guide
Previous: Contents
Contents
Index
- Graph of van der Waals potential with and without switching
- Graph of electrostatic potential with and without shifting function
- Graph of electrostatic split between short and long range forces
- Example of cutoff and pairlist distance uses
- Graph showing a slice of a ramp potential, showing the effect of
mgridforcevoff
- Graphical representation of a collective variables configuration
The colvar called ``
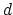 '' is defined as the difference between two distances: the first distance (
'' is defined as the difference between two distances: the first distance (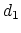 ) is taken between the center of mass of atoms 1 and 2 and that of atoms 3 to 5, the second (
) is taken between the center of mass of atoms 1 and 2 and that of atoms 3 to 5, the second (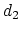 ) between atom 7 and the center of mass of atoms 8 to 10.
The difference
) between atom 7 and the center of mass of atoms 8 to 10.
The difference
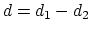 is obtained by multiplying the two by a coefficient
is obtained by multiplying the two by a coefficient 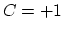 or
or 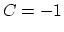 , respectively.
The colvar called ``
, respectively.
The colvar called ``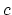 '' is the coordination number calculated between atoms 1 to 10 and atoms 11 to 20. A harmonic restraint is applied to both
'' is the coordination number calculated between atoms 1 to 10 and atoms 11 to 20. A harmonic restraint is applied to both 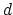 and
and 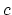 : to allow using the same force constant
: to allow using the same force constant 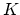 , both
, both 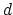 and
and 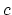 are scaled by their respective fluctuation widths
are scaled by their respective fluctuation widths 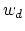 and
and 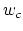 .
A third colvar ``alpha'' is defined as the
.
A third colvar ``alpha'' is defined as the 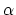 -helical content of residues 1 to 10.
The values of ``
-helical content of residues 1 to 10.
The values of ``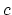 '' and ``alpha'' are also recorded throughout the simulation as a joint 2-dimensional histogram.
'' and ``alpha'' are also recorded throughout the simulation as a joint 2-dimensional histogram.
- Dual topology description for an alchemical simulation.
Case example of the mutation of alanine into serine.
The lighter color denotes the non-interacting, alternate
state.
- Convergence of an FEP calculation. If the ensembles representative
of states
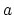 and
and 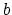 are too disparate, equation (59) will
not converge (a).
If, in sharp contrast, the configurations of
state
are too disparate, equation (59) will
not converge (a).
If, in sharp contrast, the configurations of
state 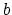 form a subset of the ensemble of configurations
characteristic of state
form a subset of the ensemble of configurations
characteristic of state 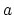 , the simulation is expected
to converge (b).
The difficulties reflected in case (a) may be
alleviated by the introduction of mutually overlapping intermediate
states that connect
, the simulation is expected
to converge (b).
The difficulties reflected in case (a) may be
alleviated by the introduction of mutually overlapping intermediate
states that connect 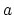 to
to 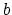 (c). It should be
mentioned that in practice, the kinetic contribution,
(c). It should be
mentioned that in practice, the kinetic contribution,
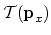 ,
is assumed to be identical for state
,
is assumed to be identical for state 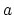 and state
and state 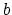 .
.
- Relationship of user-defined
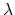 to coupling of electrostatic or vdW interactions to a simulation, given specific values of alchElecLambdaStart or alchVdwLambdaEnd.
to coupling of electrostatic or vdW interactions to a simulation, given specific values of alchElecLambdaStart or alchVdwLambdaEnd.
- Sample TI data (
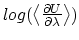 against
against 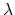 ). The blue shaded
area shows the integral with fine sampling close to the end point. The red area
shows the difference when
). The blue shaded
area shows the integral with fine sampling close to the end point. The red area
shows the difference when 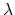 values are more sparse. In this example,
insufficient sampling before
values are more sparse. In this example,
insufficient sampling before 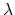
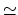 0.1 can result in a large overestimation
of the integral. Beyond
0.1 can result in a large overestimation
of the integral. Beyond 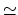 0.2, sparser sampling is justified as dE/d
0.2, sparser sampling is justified as dE/d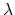 is not
changing quickly.
is not
changing quickly.
- Schematics of the aMD method. When the original potential (thick line) falls below a threshold energy
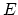 (dashed line),
a boost potential is added. The modified energy profiles (thin lines) have smaller barriers separating adjacent
energy basins.
(dashed line),
a boost potential is added. The modified energy profiles (thin lines) have smaller barriers separating adjacent
energy basins.
http://www.ks.uiuc.edu/Research/namd/