



Next: Colvars scripting
Up: Collective Variable-based Calculations1
Previous: Collective variable components (basis
Contents
Index
Subsections
Biasing and analysis methods
All of the biasing and analysis methods implemented (abf,
harmonic, histogram and metadynamics)
recognize the following options:
For a full description of the Adaptive Biasing Force method, see
reference [19]. For details about this implementation,
see references [33] and [34]. When
publishing research that makes use of this functionality, please cite
references [19] and [34].
An alternate usage of this feature is the application of custom
tabulated biasing potentials to one or more colvars. See
inputPrefix and updateBias below.
ABF is based on the thermodynamic integration (TI) scheme for
computing free energy profiles. The free energy as a function
of a set of collective variables
![$ {\mbox{\boldmath {$\xi$}}}=(\xi_{i})_{i\in[1,n]}$](img383.png) is defined from the canonical distribution of
is defined from the canonical distribution of
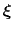 ,
,
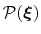 :
:
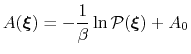 |
(48) |
In the TI formalism, the free energy is obtained from its gradient,
which is generally calculated in the form of the average of a force
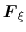 exerted on
exerted on
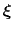 , taken over an iso-
, taken over an iso-
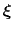 surface:
surface:
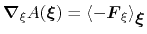 |
(49) |
Several formulae that take the form of (50) have been
proposed. This implementation relies partly on the classic
formulation [14], and partly on a more versatile scheme
originating in a work by Ruiz-Montero et al. [60],
generalized by den Otter [20] and extended to multiple
variables by Ciccotti et al. [17]. Consider a system
subject to constraints of the form
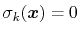 . Let
(
. Let
(
![$ {\mbox{\boldmath {$v$}}}_{i})_{i\in[1,n]}$](img390.png) be arbitrarily chosen vector fields
(
be arbitrarily chosen vector fields
(
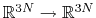 ) verifying, for all
) verifying, for all 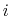 ,
,
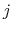 , and
, and 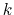 :
:
then the following holds [17]:
 |
(52) |
where 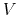 is the potential energy function.
is the potential energy function.
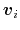 can be interpreted as the direction along which the force
acting on variable
can be interpreted as the direction along which the force
acting on variable 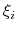 is measured, whereas the second term in the
average corresponds to the geometric entropy contribution that appears
as a Jacobian correction in the classic formalism [14].
Condition (51) states that the direction along
which the system force on
is measured, whereas the second term in the
average corresponds to the geometric entropy contribution that appears
as a Jacobian correction in the classic formalism [14].
Condition (51) states that the direction along
which the system force on 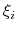 is measured is orthogonal to the
gradient of
is measured is orthogonal to the
gradient of 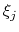 , which means that the force measured on
, which means that the force measured on 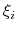 does not act on
does not act on 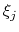 .
.
Equation (52) implies that constraint forces
are orthogonal to the directions along which the free energy gradient is
measured, so that the measurement is effectively performed on unconstrained
degrees of freedom.
In NAMD, constraints are typically applied to the lengths of
bonds involving hydrogen atoms, for example in TIP3P water molecules (parameter rigidBonds, section 5.6.1).
In the framework of ABF,
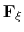 is accumulated in bins of finite size
is accumulated in bins of finite size
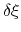 ,
thereby providing an estimate of the free energy gradient
according to equation (50).
The biasing force applied along the collective variables
to overcome free energy barriers is calculated as:
,
thereby providing an estimate of the free energy gradient
according to equation (50).
The biasing force applied along the collective variables
to overcome free energy barriers is calculated as:
where
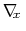
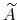 denotes the current estimate of the
free energy gradient at the current point
denotes the current estimate of the
free energy gradient at the current point
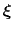 in the collective
variable subspace, and
in the collective
variable subspace, and
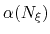 is a scaling factor that is ramped
from 0 to 1 as the local number of samples
is a scaling factor that is ramped
from 0 to 1 as the local number of samples 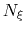 increases
to prevent nonequilibrium effects in the early phase of the simulation,
when the gradient estimate has a large variance.
See the fullSamples parameter below for details.
increases
to prevent nonequilibrium effects in the early phase of the simulation,
when the gradient estimate has a large variance.
See the fullSamples parameter below for details.
As sampling of the phase space proceeds, the estimate
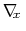
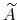 is progressively refined. The biasing
force introduced in the equations of motion guarantees that in
the bin centered around
is progressively refined. The biasing
force introduced in the equations of motion guarantees that in
the bin centered around
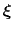 ,
the forces acting along the selected collective variables average
to zero over time. Eventually, as the undelying free energy surface is canceled
by the adaptive bias, evolution of the system along
,
the forces acting along the selected collective variables average
to zero over time. Eventually, as the undelying free energy surface is canceled
by the adaptive bias, evolution of the system along
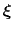 is governed mainly by diffusion.
Although this implementation of ABF can in principle be used in
arbitrary dimension, a higher-dimension collective variable space is likely
to result in sampling difficulties.
Most commonly, the number of variables is one or two.
is governed mainly by diffusion.
Although this implementation of ABF can in principle be used in
arbitrary dimension, a higher-dimension collective variable space is likely
to result in sampling difficulties.
Most commonly, the number of variables is one or two.
ABF requirements on collective variables
- Only linear combinations of colvar components can be used in ABF calculations.
- Availability of system forces is necessary. The following colvar components
can be used in ABF calculations:
distance, distance_xy, distance_z, angle,
dihedral, gyration, rmsd and eigenvector.
Atom groups may not be replaced by dummy atoms, unless they are excluded
from the force measurement by specifying oneSiteSystemForce, if available.
- Mutual orthogonality of colvars. In a multidimensional ABF calculation,
equation (51) must be satisfied for any two colvars
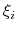 and
and 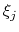 .
Various cases fulfill this orthogonality condition:
.
Various cases fulfill this orthogonality condition:
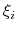 and
and 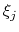 are based on non-overlapping sets of atoms.
are based on non-overlapping sets of atoms.
- atoms involved in the force measurement on
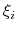 do not participate in
the definition of
do not participate in
the definition of 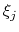 . This can be obtained using the option oneSiteSystemForce
of the distance, angle, and dihedral components
(example: Ramachandran angles
. This can be obtained using the option oneSiteSystemForce
of the distance, angle, and dihedral components
(example: Ramachandran angles 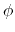 ,
, 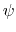 ).
).
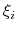 and
and 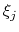 are orthogonal by construction. Useful cases are the sum and
difference of two components, or distance_z and distance_xy using the same axis.
are orthogonal by construction. Useful cases are the sum and
difference of two components, or distance_z and distance_xy using the same axis.
- Mutual orthogonality of components: when several components are combined into a colvar,
it is assumed that their vectors
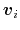 (equation (53))
are mutually orthogonal. The cases described for colvars in the previous paragraph apply.
(equation (53))
are mutually orthogonal. The cases described for colvars in the previous paragraph apply.
- Orthogonality of colvars and constraints: equation 52 can
be satisfied in two simple ways, if either no constrained atoms are involved in the force measurement
(see point 3 above) or pairs of atoms joined by a constrained bond are part of an atom group
which only intervenes through its center (center of mass or geometric center) in the force measurement.
In the latter case, the contributions of the two atoms to the left-hand side of equation 52
cancel out. For example, all atoms of a rigid TIP3P water molecule can safely be included in an atom
group used in a distance component.
ABF depends on parameters from collective variables to define the grid on which free
energy gradients are computed. In the direction of each colvar, the grid ranges from
lowerBoundary to upperBoundary, and the bin width (grid spacing)
is set by the width parameter (see 10.2.1).
The following specific parameters can be set in the ABF configuration block
(in addition to generic bias parameters such as colvars
- section 10.5):
- fullSamples
 Number of samples in a bin prior
to application of the ABF
Number of samples in a bin prior
to application of the ABF 
Context: abf
Acceptable Values: positive integer
Default Value: 200
Description: To avoid nonequilibrium effects due to large fluctuations of the force exerted along the
colvars, it is recommended to apply a biasing force only after a the estimate has started
converging. If fullSamples is non-zero, the applied biasing force is scaled by a factor
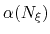 between 0 and 1.
If the number of samples
between 0 and 1.
If the number of samples 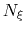 in the current bin is higher than fullSamples,
the factor is one. If it is less than half of fullSamples, the factor is zero and
no bias is applied. Between those two thresholds, the factor follows a linear ramp from
0 to 1:
in the current bin is higher than fullSamples,
the factor is one. If it is less than half of fullSamples, the factor is zero and
no bias is applied. Between those two thresholds, the factor follows a linear ramp from
0 to 1:
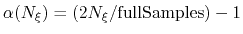 .
.
- maxForce
 Maximum magnitude of the ABF force
Maximum magnitude of the ABF force 
Context: abf
Acceptable Values: positive decimals (one per colvar)
Default Value: disabled
Description: This option enforces a cap on the magnitude of the biasing force effectively applied
by this ABF bias on each colvar. This can be useful in the presence of singularities
in the PMF such as hard walls, where the discretization of the average force becomes
very inaccurate, causing the colvar's diffusion to get ``stuck'' at the singularity.
To enable this cap, provide one non-negative value for each colvar. The unit of force
is kcal/mol divided by the colvar unit (Å for lengths, degrees for angles, etc.).
- hideJacobian
 Remove geometric entropy term from calculated
free energy gradient?
Remove geometric entropy term from calculated
free energy gradient? 
Context: abf
Acceptable Values: boolean
Default Value: no
Description: In a few special cases, most notably distance-based variables, an alternate definition of
the potential of mean force is traditionally used, which excludes the Jacobian
term describing the effect of geometric entropy on the distribution of the variable.
This results, for example, in particle-particle potentials of mean force being flat
at large separations.
Setting this parameter to yes causes the output data to follow that convention,
by removing this contribution from the output gradients while
applying internally the corresponding correction to ensure uniform sampling.
It is not allowed for colvars with multiple components.
- outputFreq
 Frequency (in timesteps) at which ABF data files are refreshed
Frequency (in timesteps) at which ABF data files are refreshed 
Context: abf
Acceptable Values: positive integer
Default Value: Colvar module restart frequency
Description: The files containing the free energy gradient estimate and sampling histogram
(and the PMF in one-dimensional calculations) are written on disk at the given
time interval.
- historyFreq
 Frequency (in timesteps) at which ABF history files are
accumulated
Frequency (in timesteps) at which ABF history files are
accumulated 
Context: abf
Acceptable Values: positive integer
Default Value: 0
Description: If this number is non-zero, the free energy gradient estimate and sampling histogram
(and the PMF in one-dimensional calculations) are appended to files on disk at
the given time interval. History file names use the same prefix as output files, with
``.hist'' appended.
- inputPrefix
 Filename prefix for reading ABF data
Filename prefix for reading ABF data 
Context: abf
Acceptable Values: list of strings
Description: If this parameter is set, for each item in the list, ABF tries to read
a gradient and a sampling files named  inputPrefix
inputPrefix .grad
and
.grad
and  inputPrefix
inputPrefix .count. This is done at
startup and sets the initial state of the ABF algorithm.
The data from all provided files is combined appropriately.
Also, the grid definition (min and max values, width) need not be the same
that for the current run. This command is useful to piece together
data from simulations in different regions of collective variable space,
or change the colvar boundary values and widths. Note that it is not
recommended to use it to switch to a smaller width, as that will leave
some bins empty in the finer data grid.
This option is NOT compatible with reading the data from a restart file (colvarsInput option of the NAMD config file).
.count. This is done at
startup and sets the initial state of the ABF algorithm.
The data from all provided files is combined appropriately.
Also, the grid definition (min and max values, width) need not be the same
that for the current run. This command is useful to piece together
data from simulations in different regions of collective variable space,
or change the colvar boundary values and widths. Note that it is not
recommended to use it to switch to a smaller width, as that will leave
some bins empty in the finer data grid.
This option is NOT compatible with reading the data from a restart file (colvarsInput option of the NAMD config file).
- applyBias
 Apply the ABF bias?
Apply the ABF bias? 
Context: abf
Acceptable Values: boolean
Default Value: yes
Description: If this is set to no, the calculation proceeds normally but the adaptive
biasing force is not applied. Data is still collected to compute
the free energy gradient. This is mostly intended for testing purposes, and should
not be used in routine simulations.
- updateBias
 Update the ABF bias?
Update the ABF bias? 
Context: abf
Acceptable Values: boolean
Default Value: yes
Description: If this is set to no, the initial biasing force (e.g. read from a restart fileor through inputPrefix) is not updated during the simulation.
As a result, a constant bias is applied. This can be used to apply a custom, tabulated
biasing potential to any combination of colvars. To that effect, one should prepare
a gradient file containing the gradient of the potential to be applied (negative
of the bias force), and a count file containing only values greater than
fullSamples. These files must match the grid parameters of the colvars.
The ABF bias produces the following files, all in multicolumn ASCII format:
- outputName.grad: current estimate of the free energy gradient (grid),
in multicolumn;
- outputName.count: total number of samples collected, on the same grid;
- outputName.pmf: only for one-dimensional calculations, integrated
free energy profile or PMF.
If several ABF biases are defined concurrently, their name is inserted to produce
unique filenames for output, as in outputName.abf1.grad.
This should not be done routinely and could lead to meaningless results:
only do it if you know what you are doing!
If the colvar space has been partitioned into sections (windows) in which independent
ABF simulations have been run, the resulting data can be merged using the
inputPrefix option described above (a NAMD run of 0 steps is enough).
If a one-dimensional calculation is performed, the estimated free energy
gradient is automatically integrated and a potential of mean force is written
under the file name <outputName>.pmf, in a plain text format that
can be read by most data plotting and analysis programs (e.g. gnuplot).
In dimension 2 or greater, integrating the discretized gradient becomes non-trivial. The
standalone utility abf_integrate is provided to perform that task.
abf_integrate reads the gradient data and uses it to perform a Monte-Carlo (M-C)
simulation in discretized collective variable space (specifically, on the same grid
used by ABF to discretize the free energy gradient).
By default, a history-dependent bias (similar in spirit to metadynamics) is used:
at each M-C step, the bias at the current position is incremented by a preset amount
(the hill height).
Upon convergence, this bias counteracts optimally the underlying gradient;
it is negated to obtain the estimate of the free energy surface.
abf_integrate is invoked using the command-line:
integrate <gradient_file> [-n <nsteps>] [-t <temp>] [-m (0|1)]
[-h <hill_height>] [-f <factor>]
The gradient file name is provided first, followed by other parameters in any order.
They are described below, with their default value in square brackets:
- -n: number of M-C steps to be performed; by default, a minimal number of
steps is chosen based on the size of the grid, and the integration runs until a convergence
criterion is satisfied (based on the RMSD between the target gradient and the real PMF gradient)
- -t: temperature for M-C sampling (unrelated to the simulation temperature)
[500 K]
- -m: use metadynamics-like biased sampling? (0 = false) [1]
- -h: increment for the history-dependent bias (``hill height'') [0.01 kcal/mol]
- -f: if non-zero, this factor is used to scale the increment stepwise in the
second half of the M-C sampling to refine the free energy estimate [0.5]
Using the default values of all parameters should give reasonable results in most cases.
abf_integrate produces the following output files:
- <gradient_file>.pmf: computed free energy surface
- <gradient_file>.histo: histogram of M-C sampling (not
usable in a straightforward way if the history-dependent bias has been applied)
- <gradient_file>.est: estimated gradient of the calculated free energy surface
(from finite differences)
- <gradient_file>.dev: deviation between the user-provided numerical gradient
and the actual gradient of the calculated free energy surface. The RMS norm of this vector
field is used as a convergence criteria and displayed periodically during the integration.
Note: Typically, the ``deviation'' vector field does not
vanish as the integration converges. This happens because the
numerical estimate of the gradient does not exactly derive from a
potential, due to numerical approximations used to obtain it (finite
sampling and discretization on a grid).
Metadynamics
The metadynamics method uses a history-dependent potential [42] that generalizes to any type of colvars the conformational flooding [27] and local elevation [35] methods, originally formulated to use as colvars the principal components of a covariance matrix or a set of dihedral angles, respectively.
The metadynamics potential on the colvars
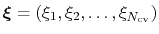 is defined as:
is defined as:
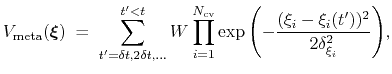 |
(54) |
where
 is the history-dependent potential acting on the current values of the colvars
is the history-dependent potential acting on the current values of the colvars
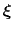 , and depends only parametrically on the previous values of the colvars.
, and depends only parametrically on the previous values of the colvars.
 is constructed as a sum of
is constructed as a sum of
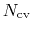 -dimensional repulsive Gaussian ``hills'', whose height is a chosen energy constant
-dimensional repulsive Gaussian ``hills'', whose height is a chosen energy constant 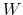 , and whose centers are the previously explored configurations
, and whose centers are the previously explored configurations
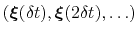 .
Each Gaussian functions has a width of approximately
.
Each Gaussian functions has a width of approximately
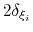 along the direction of the
along the direction of the 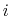 -th colvar.
-th colvar.
During the simulation, the system evolves towards the nearest minimum of the ``effective'' potential of mean force
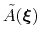 , which is the sum of the ``real'' underlying potential of mean force
, which is the sum of the ``real'' underlying potential of mean force
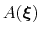 and the the metadynamics potential
and the the metadynamics potential
 .
Therefore, at any given time the probability of observing the configuration
.
Therefore, at any given time the probability of observing the configuration
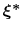 is proportional to
is proportional to
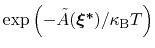 : this is also the probability that a new Gaussian ``hill'' is added at that configuration.
If the simulation is run for a sufficiently long time, each local minimum is canceled out by the sum of the Gaussian ``hill'' functions.
At that stage the the ``effective'' potential of mean force
: this is also the probability that a new Gaussian ``hill'' is added at that configuration.
If the simulation is run for a sufficiently long time, each local minimum is canceled out by the sum of the Gaussian ``hill'' functions.
At that stage the the ``effective'' potential of mean force
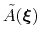 is constant, and
is constant, and
 is an accurate estimator of the ``real'' potential of mean force
is an accurate estimator of the ``real'' potential of mean force
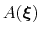 , save for an additive constant:
, save for an additive constant:
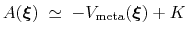 |
(55) |
Assuming that the set of collective variables includes all relevant degrees of freedom, the predicted error of the estimate is a simple function of the correlation times of the colvars
 , and of the user-defined parameters
, and of the user-defined parameters 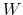 ,
,
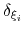 and
and 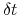 [13].
In typical applications, a good rule of thumb can be to choose the ratio
[13].
In typical applications, a good rule of thumb can be to choose the ratio
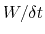 much smaller than
much smaller than
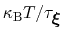 , where
, where
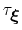 is the longest among
is the longest among
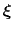 's correlation times:
's correlation times:
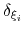 then dictates the resolution of the calculated PMF.
then dictates the resolution of the calculated PMF.
To enable a metadynamics calculation, a metadynamics block must be defined in the colvars configuration file.
Its only mandatory keyword is the colvars option listing all the variables involved: multidimensional PMFs are obtained by the same metadynamics instance applied to all the colvars.
The parameters 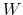 and
and 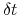 are specified by the keywords hillWeight and newHillFrequency, respectively.
The values of these options are optimal for colvars with correlation times
are specified by the keywords hillWeight and newHillFrequency, respectively.
The values of these options are optimal for colvars with correlation times
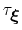 in the range of a few thousand simulation steps, typical of many biomolecular simulations:
in the range of a few thousand simulation steps, typical of many biomolecular simulations:
It is the user's responsibility to either leave hillWeight and newHillFrequency at their default values, or to change them to match the specifics of each system.
The parameter
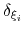 is instead defined as approximately half the width of the corresponding colvar
is instead defined as approximately half the width of the corresponding colvar 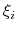 (see 10.2.1).
(see 10.2.1).
Output files
When interpolating grids are enabled (default behavior), the PMF is written every colvarsRestartFrequency steps to the file outputName.pmf.
The following two options allow to control this behavior and to visually track statistical convergence:
Note: when Gaussian hills are deposited near lowerBoundary or upperBoundary (see 10.2.1) and interpolating grids are used (default behavior), their truncation can give rise to accumulating errors.
In these cases, as a measure of fault-tolerance all Gaussian hills near the boundaries are included in the output state file, and are recalculated analytically whenever the colvar falls outside the grid's boundaries.
(Such measure protects the accuracy of the calculation, and can only be disabled by hardLowerBoundary or hardUpperBoundary.)
To avoid gradual loss of performance and growth of the state file, either one of the following solutions is recommended:
- enabling the option expandBoundaries, so that the grid's boundaries are automatically recalculated whenever necessary; the resulting .pmf will have its abscissas expanded accordingly;
- setting lowerWall and upperWall well within the interval delimited by lowerBoundary and upperBoundary.
Performance tuning
The following options control the computational cost of metadynamics calculations, but do not affect results.
Default values are chosen to minimize such cost with no loss of accuracy.
Well-tempered metadynamics
The following options define the configuration for the ``well-tempered'' metadynamics approach [4]:
Multiple-replicas metadynamics
The following options define metadynamics calculations with more than
one replica:
- multipleReplicas
 Multiple replicas metadynamics
Multiple replicas metadynamics 
Context: metadynamics
Acceptable Values: boolean
Default Value: off
Description: If this option is on, multiple (independent) replica of the
same system can be run at the same time, and their hills will be
combined to obtain a single PMF [58]. Replicas are
identified by the value of replicaID. Communication is
done by files: each replica must be able to read the files
created by the others, whose paths are communicated through the file
replicasRegistry. This file, and the files listed in it,
are read every replicaUpdateFrequency steps. Every time
the colvars state file is written
(colvarsRestartFrequency), the file:
``outputName.colvars.name.replicaID.state''
is also written, containing
the state of the metadynamics bias for replicaID. In the
time steps between colvarsRestartFrequency, new hills are
temporarily written to the file:
``outputName.colvars.name.replicaID.hills'',
which serves as communication
buffer. These files are only required for communication, and may be
deleted after a new MD run is started with a different
outputName.
- replicaID
 Set the identifier for this replica
Set the identifier for this replica 
Context: metadynamics
Acceptable Values: string
Description: If multipleReplicas is on, this option sets a
unique identifier for this replica. All replicas should use
identical collective variable configurations, except for the value
of this option.
- replicasRegistry
 Multiple replicas database file
Multiple replicas database file 
Context: metadynamics
Acceptable Values: UNIX filename
Default Value: ``name.replica_files.txt''
Description: If multipleReplicas is on, this option sets the
path to the replicas' database file.
- replicaUpdateFrequency
 How often hills are communicated between
replicas
How often hills are communicated between
replicas 
Context: metadynamics
Acceptable Values: positive integer
Default Value: newHillFrequency
Description: If multipleReplicas is on, this option sets the
number of steps after which each replica (re)reads the other
replicas' files. The lowest meaningful value of this number is
newHillFrequency. If access to the file system is
significantly affecting the simulation performance, this number can
be increased, at the price of reduced synchronization between
replicas. Values higher than colvarsRestartFrequency may
not improve performance significantly.
- dumpPartialFreeEnergyFile
 Periodically write the contribution to the
PMF from this replica
Periodically write the contribution to the
PMF from this replica 
Context: metadynamics
Acceptable Values: boolean
Default Value: on
Description: When multipleReplicas is on, tje file
outputName.pmf contains the combined PMF from all
replicas. Enabling this option produces an additional file
outputName.partial.pmf, which can be useful to
quickly monitor the contribution of each replica to the PMF. The
requirements for this option are the same as
dumpFreeEnergyFile.
The following options may be useful only for applications that go beyond the calculation of a PMF by metadynamics:
- name
 Name of this metadynamics instance
Name of this metadynamics instance 
Context: metadynamics
Acceptable Values: string
Default Value: ``meta'' + rank number
Description: This option sets the name for this metadynamics instance. While it
is not advisable to use more than one metadynamics instance within
the same simulation, this allows to distinguish each instance from
the others. If there is more than one metadynamics instance, the
name of this bias is included in the metadynamics output file names, such as e.g. the .pmf file.
- keepHills
 Write each individual hill to the state
file
Write each individual hill to the state
file 
Context: metadynamics
Acceptable Values: boolean
Default Value: off
Description: When useGrids and this option are on, all hills
are saved to the state file in their analytic form, alongside their
grids. This makes it possible to later use exact analytic Gaussians
for rebinGrids. To only keep track of the history of the
added hills, writeHillsTrajectory is preferable.
- writeHillsTrajectory
 Write a log of new hills
Write a log of new hills 
Context: metadynamics
Acceptable Values: boolean
Default Value: on
Description: If this option is on, a logfile is written by the
metadynamics bias, with the name
``outputName.colvars. name
name .hills.traj'', which
can be useful to follow the time series of the hills. When
multipleReplicas is on, its name changes to
.hills.traj'', which
can be useful to follow the time series of the hills. When
multipleReplicas is on, its name changes to
``outputName.colvars. name
name .
. replicaID
replicaID .hills.traj''.
This file can be used to quickly visualize the positions of all
added hills, in case newHillFrequency does not coincide
with colvarsRestartFrequency.
.hills.traj''.
This file can be used to quickly visualize the positions of all
added hills, in case newHillFrequency does not coincide
with colvarsRestartFrequency.
Harmonic restraints
The harmonic biasing method may be used to enforce fixed or moving restraints,
including variants of Steered and Targeted MD. Within energy minimization
runs, it allows for restrained minimization, e.g. to calculate relaxed potential
energy surfaces. In the context of the colvars module,
harmonic potentials are meant according to their textbook definition:
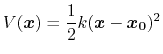 .
Note that this differs from harmonic bond and angle potentials in common
force fields, where the factor of one half is typically omitted,
resulting in a non-standard definition of the force constant.
The restraint energy is reported by NAMD under the MISC title.
A harmonic restraint is set up by a harmonic {...}
block, which may contain (in addition to the standard option
colvars) the following keywords:
.
Note that this differs from harmonic bond and angle potentials in common
force fields, where the factor of one half is typically omitted,
resulting in a non-standard definition of the force constant.
The restraint energy is reported by NAMD under the MISC title.
A harmonic restraint is set up by a harmonic {...}
block, which may contain (in addition to the standard option
colvars) the following keywords:
- forceConstant
 Scaled force constant (kcal/mol)
Scaled force constant (kcal/mol) 
Context: harmonic
Acceptable Values: positive decimal
Default Value: 1.0
Description: This defines a scaled force constant for the harmonic potential.
To ensure consistency for multidimensional restraints, it is
divided internally by the square of the specific width
for each colvar involved (which is 1 by default), so that all colvars
are effectively dimensionless and of commensurate size.
For instance, setting a scaled force constant of 10 kcal/mol acting
on two colvars, an angle with a width of 5 degrees and a distance
with a width of 0.5 Å, will apply actual force constants of
0.4 kcal/mol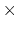 degree
degree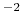 for the angle and
40 kcal/mol/Å
for the angle and
40 kcal/mol/Å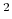 for the distance.
for the distance.
- centers
 Initial harmonic restraint centers
Initial harmonic restraint centers 
Context: harmonic
Acceptable Values: space-separated list of colvar values
Description: The centers (equilibrium values) of the restraint are entered here.
The number of values must be the number of requested colvars.
Each value is a decimal number if the corresponding colvar returns
a scalar, a ``(x, y, z)'' triplet if it returns a unit
vector or a vector, and a ``q0, q1, q2, q3)'' quadruplet
if it returns a rotational quaternion. If a colvar has
periodicities or symmetries, its closest image to the restraint
center is considered when calculating the harmonic potential.
Tip: A complex set of restraints can be applied to a system,
by defining several colvars, and applying one or more harmonic
restraints to different groups of colvars. In some cases, dozens of
colvars can be defined, but their value may not be relevant: to
limit the size of the colvars trajectory file, it
may be wise to disable outputValue for such ``ancillary''
variables, and leave it enabled only for ``relevant'' ones.
Moving restraints: steered molecular dynamics
The following options allow to change gradually the centers of the harmonic restraints during a simulations.
When the centers are changed continuously, a steered MD in a collective variable space is carried out.
- targetCenters
 Steer the restraint centers towards these
targets
Steer the restraint centers towards these
targets 
Context: harmonic
Acceptable Values: space-separated list of colvar values
Description: When defined, the current centers will be moved towards
these values during the simulation.
By default, the centers are moved over a total of
targetNumSteps steps by a linear interpolation, in the
spirit of Steered MD.
If targetNumStages is set to a nonzero value, the
change is performed in discrete stages, lasting targetNumSteps
steps each. This second mode may be used to sample successive
windows in the context
of an Umbrella Sampling simulation.
When continuing a simulation
run, the centers specified in the configuration file
 colvarsConfig
colvarsConfig are overridden by those saved in
the restart file
are overridden by those saved in
the restart file  colvarsInput
colvarsInput . To perform Steered
MD in an arbitrary space of colvars, it is
sufficient to use this option and enable
outputAppliedForce within each of the colvars involved.
. To perform Steered
MD in an arbitrary space of colvars, it is
sufficient to use this option and enable
outputAppliedForce within each of the colvars involved.
- targetNumSteps
 Number of steps for steering
Number of steps for steering 
Context: harmonic
Acceptable Values: positive integer
Description: In single-stage (continuous) transformations, defines the number of MD
steps required to move the restraint centers (or force constant)
towards the values specified with targetCenters or
targetForceConstant.
After the target values have been reached, the centers (resp. force
constant) are kept fixed. In multi-stage transformations, this sets the
number of MD steps per stage.
- outputCenters
 Write the current centers to the trajectory file
Write the current centers to the trajectory file 
Context: harmonic
Acceptable Values: boolean
Default Value: off
Description: If this option is chosen and colvarsTrajFrequency is not zero, the positions of the restraint centers will be written to the trajectory file during the simulation.
This option allows to conveniently extract the PMF from the colvars trajectory files in a steered MD calculation.
- outputAccumulatedWork
 Write the accumulated work of the moving restraint to the trajectory file
Write the accumulated work of the moving restraint to the trajectory file 
Context: harmonic
Acceptable Values: boolean
Default Value: off
Description: If this option is chosen, targetCenters is defined, and colvarsTrajFrequency is not zero, the accumulated work from the beginning of the simulation will be written to the trajectory file.
If the simulation has been continued from a previous state file, the previously accumulated work is included in the integral.
This option allows to conveniently extract the PMF from the colvars trajectory files in a steered MD calculation.
Note on restarting moving restraint simulations: Information
about the current step and stage of a simulation with moving restraints
is stored in the restart file (state file). Thus, such simulations can
be run in several chunks, and restarted directly using the same colvars
configuration file. In case of a restart, the values of parameters such
as targetCenters, targetNumSteps, etc. should not be
changed manually.
Moving restraints: umbrella sampling
The centers of the harmonic restraints can also be changed in discrete stages: in this cases a one-dimensional umbrella sampling simulation is performed.
The sampling windows in simulation are calculated in sequence.
The colvars trajectory file may then be used both to evaluate the correlation times between consecutive windows, and to calculate the frequency distribution of the colvar of interest in each window.
Furthermore, frequency distributions on a predefined grid can be automatically obtained by using the histogram bias (see 10.5.6).
To activate an umbrella sampling simulation, the same keywords as in the previous section can be used, with the addition of the following:
Changing force constant
The force constant of the harmonic restraint may also be changed to equilibrate [21].
- targetForceConstant
 Change the force constant towards this value
Change the force constant towards this value 
Context: harmonic
Acceptable Values: positive decimal
Description: When defined, the current forceConstant will be moved towards
this value during the simulation. Time evolution of the force constant
is dictated by the targetForceExponent parameter (see below).
By default, the force constant is changed smoothly over a total of
targetNumSteps steps. This is useful to introduce or
remove restraints in a progressive manner.
If targetNumStages is set to a nonzero value, the
change is performed in discrete stages, lasting targetNumSteps
steps each. This second mode may be used to compute the
conformational free energy change associated with the restraint, within
the FEP or TI formalisms. For convenience, the code provides an estimate
of the free energy derivative for use in TI. A more complete free energy
calculation (particularly with regard to convergence analysis),
while not handled by the colvars module, can be performed by post-processing
the colvars trajectory, if colvarsTrajFrequency is set to a
suitably small value. It should be noted, however, that restraint
free energy calculations may be handled more efficiently by an
indirect route, through the
determination of a PMF for the restrained coordinate.[21]
- targetForceExponent
 Exponent in the time-dependence of the force constant
Exponent in the time-dependence of the force constant 
Context: harmonic
Acceptable Values: decimal equal to or greater than 1.0
Default Value: 1.0
Description: Sets the exponent, 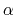 , in the function used to vary the force
constant as a function of time. The force is varied according to a
coupling parameter
, in the function used to vary the force
constant as a function of time. The force is varied according to a
coupling parameter 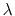 , raised to the power
, raised to the power 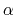 :
:
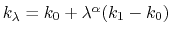 , where
, where 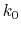 ,
,
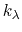 , and
, and 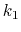 are the initial, current, and final values
of the force constant. The parameter
are the initial, current, and final values
of the force constant. The parameter 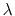 evolves linearly from
0 to 1, either smoothly, or in targetNumStages equally spaced
discrete stages, or according to an arbitrary schedule set with
lambdaSchedule.
When the initial value of the force constant is zero,
an exponent greater than 1.0 distributes the effects of introducing the
restraint more smoothly over time than a linear dependence, and
ensures that there is no singularity in the derivative of the
restraint free energy with respect to lambda. A value of 4 has
been found to give good results in some tests.
evolves linearly from
0 to 1, either smoothly, or in targetNumStages equally spaced
discrete stages, or according to an arbitrary schedule set with
lambdaSchedule.
When the initial value of the force constant is zero,
an exponent greater than 1.0 distributes the effects of introducing the
restraint more smoothly over time than a linear dependence, and
ensures that there is no singularity in the derivative of the
restraint free energy with respect to lambda. A value of 4 has
been found to give good results in some tests.
- targetEquilSteps
 Number of steps discarded from TI estimate
Number of steps discarded from TI estimate 
Context: harmonic
Acceptable Values: positive integer
Description: Defines the number of steps within each stage that are considered
equilibration and discarded from the restraint free energy derivative
estimate reported reported in the output.
- lambdaSchedule
 Schedule of lambda-points for changing force constant
Schedule of lambda-points for changing force constant 
Context: harmonic
Acceptable Values: list of real numbers between 0 and 1
Description: If specified together with targetForceConstant, sets the sequence of
discrete 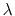 values that will be used for different stages.
values that will be used for different stages.
Linear restraints
The linear restraint biasing method is used to minimally bias a
simulation. There is generally a unique strength of bias for each CV
center, which means you must know the bias force constant specifically
for the center of the CV. This force constant may be found by using
experiment directed simulation described in
section 10.5.5. Please cite Pitera and Chodera when
using [57].
- forceConstant
 Scaled force constant (kcal/mol)
Scaled force constant (kcal/mol) 
Context: linear
Acceptable Values: positive decimal
Default Value: 1.0
Description: This defines a scaled force constant for the linear bias.
To ensure consistency for multidimensional restraints, it is
divided internally by the specific width
for each colvar involved (which is 1 by default), so that all colvars
are effectively dimensionless and of commensurate size.
- centers
 Initial linear restraint centers
Initial linear restraint centers 
Context: linear
Acceptable Values: space-separated list of colvar values
Description: The centers (equilibrium values) of the restraint are entered here.
The number of values must be the number of requested colvars.
Each value is a decimal number if the corresponding colvar returns
a scalar, a ``(x, y, z)'' triplet if it returns a unit
vector or a vector, and a ``q0, q1, q2, q3)'' quadruplet
if it returns a rotational quaternion. If a colvar has
periodicities or symmetries, its closest image to the restraint
center is considered when calculating the linear potential.
Adaptive Linear Bias/Experiment Directed Simulation
Experiment directed simulation applies a linear bias with a changing
force constant. Please cite White and Voth [75] when
using. As opposed to that reference, the force constant here is scaled
by the width corresponding to the biased colvar. In White and
Voth, each force constant is scaled by the colvars set center. The
bias converges to a linear bias, after which it will be the minimal
possible bias. You may also stop the simulation, take the median of
the force constants (ForceConst) found in the colvars trajectory file,
and then apply a linear bias with that constant. All the notes about
units described in sections 10.5.4
and 10.5.3 apply here as well. This is not
a valid simulation of any particular statistical ensemble and is only
an optimization algorithm until the bias has converged.
- centers
 Collective variable centers
Collective variable centers 
Context: alb
Acceptable Values: space-separated list of colvar values
Description: The desired center (equilibrium values) which will be sought during the
adaptive linear biasing.
The number of values must be the number of requested colvars.
Each value is a decimal number if the corresponding colvar returns
a scalar, a ``(x, y, z)'' triplet if it returns a unit
vector or a vector, and a ``q0, q1, q2, q3)'' quadruplet
if it returns a rotational quaternion. If a colvar has
periodicities or symmetries, its closest image to the restraint
center is considered when calculating the linear potential.
- updateFrequency
 The duration of updates
The duration of updates 
Context: alb
Acceptable Values: An integer
Description: This is, 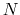 , the number of simulation steps to use for each update to the bias.
This determines how long the system requires to equilibrate
after a change in force constant (
, the number of simulation steps to use for each update to the bias.
This determines how long the system requires to equilibrate
after a change in force constant ( ), how long statistics
are collected for an iteration (
), how long statistics
are collected for an iteration ( ), and how quickly energy is
added to the system (at most,
), and how quickly energy is
added to the system (at most, 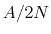 , where
, where 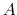 is the forceRange). Until the force
constant has converged, the method as described is an
optimization procedure and not an integration of a particular
statistical ensemble. It is important that each step should be
uncorrelated from the last so that iterations are independent.
Therefore,
is the forceRange). Until the force
constant has converged, the method as described is an
optimization procedure and not an integration of a particular
statistical ensemble. It is important that each step should be
uncorrelated from the last so that iterations are independent.
Therefore, 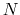 should be at least twice the autocorrelation time
of the collective variable. The system should also be able to
dissipate energy as fast as
should be at least twice the autocorrelation time
of the collective variable. The system should also be able to
dissipate energy as fast as  , which can be done by adjusting
thermostat parameters. Practically,
, which can be done by adjusting
thermostat parameters. Practically, 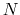 has been tested successfully at
significantly shorter than the autocorrelation time of the
collective variables being biased and still converge correctly.
has been tested successfully at
significantly shorter than the autocorrelation time of the
collective variables being biased and still converge correctly.
- forceRange
 The expected range of the force constant in units of energy
The expected range of the force constant in units of energy 
Context: alb
Acceptable Values: A space-separated list of decimal numbers
Default Value: 3 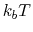
Description: This is largest magnitude of the force constant which one expects. If this parameter is
too low, the simulation will not converge. If it is too high the
simulation will waste time exploring values that are too
large. A value of 3 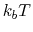 has worked well in the systems presented
as a first choice. This parameter is dynamically adjusted over
the course of a simulation. The benefit is that a bad guess for
the forceRange can be corrected. However, this can lead to
large amounts of energy being added over time to the system. To
prevent this dynamic update, add hardForceRange yes
as a parameter
has worked well in the systems presented
as a first choice. This parameter is dynamically adjusted over
the course of a simulation. The benefit is that a bad guess for
the forceRange can be corrected. However, this can lead to
large amounts of energy being added over time to the system. To
prevent this dynamic update, add hardForceRange yes
as a parameter
- rateMax
 The maximum rate of change of force constant
The maximum rate of change of force constant 
Context: alb
Acceptable Values: A list of space-separated real numbers
Description: This optional parameter controls
how much energy is added to the system from this bias. Tuning
this separately from the updateFrequency
and forceRange can allow for large bias changes but
with a low rateMax prevents large energy changes that
can lead to instability in the simulation.
Multidimensional histograms
The histogram feature is used to record the distribution of a set of collective
variables in the form of a N-dimensional histogram.
It functions as a ``collective variable bias'', and is invoked by adding a
histogram block to the colvars configuration file.
In addition to the common parameters name and colvars
described above, a histogram block may define the following parameter:
- outputFreq
 Frequency (in timesteps) at which the histogram file is refreshed
Frequency (in timesteps) at which the histogram file is refreshed 
Context: histogram
Acceptable Values: positive integer
Default Value: Colvar module restart frequency
Description: The file containing histogram data is written on disk at the given time interval.
Like the ABF and metadynamics biases, histogram uses
parameters from the colvars to define its grid. The grid ranges from
lowerBoundary to upperBoundary, and the bin width is
set by the width parameter.
Scripted biases
Rather than using the biasing methods described above, it is possible to apply biases
provided at run time as a Tcl script, in the spirit of TclForces.
- scriptedColvarForces
 Enable custom, scripted forces on colvars
Enable custom, scripted forces on colvars 
Context: global
Acceptable Values: boolean
Default Value: off
Description: If this flag is enabled, a Tcl procedure named calc_colvar_forces
accepting one parameter should be defined by the user. It is executed
at each timestep, with the current step number as parameter, between the
calculation of colvars and the application of bias forces. This procedure
may use the scripting interface (see 10.6) to access
the values of colvars and apply forces on them, effectively defining custom
collective variable biases.




Next: Colvars scripting
Up: Collective Variable-based Calculations1
Previous: Collective variable components (basis
Contents
Index
http://www.ks.uiuc.edu/Research/namd/
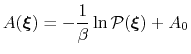

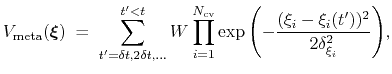
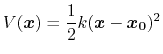 .
Note that this differs from harmonic bond and angle potentials in common
force fields, where the factor of one half is typically omitted,
resulting in a non-standard definition of the force constant.
The restraint energy is reported by NAMD under the MISC title.
A harmonic restraint is set up by a harmonic {...}
block, which may contain (in addition to the standard option
colvars) the following keywords:
.
Note that this differs from harmonic bond and angle potentials in common
force fields, where the factor of one half is typically omitted,
resulting in a non-standard definition of the force constant.
The restraint energy is reported by NAMD under the MISC title.
A harmonic restraint is set up by a harmonic {...}
block, which may contain (in addition to the standard option
colvars) the following keywords: