



Next: General parameters and input/output
Up: NAMD 2.10 User's Guide
Previous: External Program Forces
Contents
Index
Collective Variable-based Calculations1
In today's molecular dynamics simulations, it is often useful to reduce the large number of degrees of freedom of a physical system into few parameters whose statistical distributions can be analyzed individually, or used to define biasing potentials to alter the dynamics of the system in a controlled manner.
These have been called `order parameters', `collective variables', `(surrogate) reaction coordinates', and many other terms.
Here we use primarily the term `collective variable' (shortened to colvar), which indicates any differentiable function of atomic Cartesian coordinates,
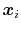 , with
, with 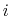 between
between 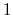 and
and 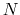 , the total
number of atoms:
, the total
number of atoms:
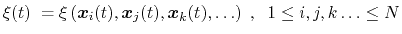 |
(35) |
The colvars module in NAMD may be used in both MD simulations and energy minimization runs.
The module is designed to perform multiple tasks concurrently, the most common of which are:
- apply restraints or biasing potentials to multiple colvars, tailored on the system by choosing from a wide set of basis functions, without limitations on their number or on the number of atoms involved; while this can in principle be done through a TclForces script, using the colvars is both easier and computationally more efficient;
- calculate potentials of mean force (PMFs) along any set of colvars, using different enhanced sampling methods, such as Adaptive Biasing Force (ABF), metadynamics, steered MD and umbrella sampling; variants of these methods that make use of an ensemble of replicas are supported as well;
- calculate statistical properties of the colvars, such as running averages and standard deviations, correlation functions of pairs of colvars, and multidimensional histograms, without the need to save very large trajectory files ;
- analyze an existing MD trajectory in terms of colvars: use NAMD's coorfile read command, and perform a 0-timestep run for each set of coordinates, as illustrated in 16.
To briefly illustrate the flexibility of the colvars module, Figure 6 shows an example of a non-trivial configuration (the corresponding input can be found in 10.1.2).
Figure 6:
Graphical representation of a collective variables configuration
The colvar called `` '' is defined as the difference between two distances: the first distance (
'' is defined as the difference between two distances: the first distance ( ) is taken between the center of mass of atoms 1 and 2 and that of atoms 3 to 5, the second (
) is taken between the center of mass of atoms 1 and 2 and that of atoms 3 to 5, the second (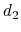 ) between atom 7 and the center of mass of atoms 8 to 10.
The difference
) between atom 7 and the center of mass of atoms 8 to 10.
The difference
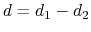 is obtained by multiplying the two by a coefficient
is obtained by multiplying the two by a coefficient 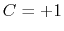 or
or 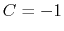 , respectively.
The colvar called ``
, respectively.
The colvar called ``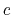 '' is the coordination number calculated between atoms 1 to 10 and atoms 11 to 20. A harmonic restraint is applied to both
'' is the coordination number calculated between atoms 1 to 10 and atoms 11 to 20. A harmonic restraint is applied to both 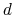 and
and 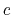 : to allow using the same force constant
: to allow using the same force constant 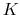 , both
, both 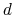 and
and 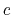 are scaled by their respective fluctuation widths
are scaled by their respective fluctuation widths 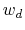 and
and 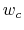 .
A third colvar ``alpha'' is defined as the
.
A third colvar ``alpha'' is defined as the 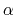 -helical content of residues 1 to 10.
The values of ``
-helical content of residues 1 to 10.
The values of ``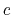 '' and ``alpha'' are also recorded throughout the simulation as a joint 2-dimensional histogram.
'' and ``alpha'' are also recorded throughout the simulation as a joint 2-dimensional histogram.
|
|
Detailed explanations of the design of the colvars module are provided in reference [22]. Please cite this reference whenever publishing work that makes use of this module.
Subsections




Next: General parameters and input/output
Up: NAMD 2.10 User's Guide
Previous: External Program Forces
Contents
Index
http://www.ks.uiuc.edu/Research/namd/
![]() , with
, with ![]() between
between ![]() and
and ![]() , the total
number of atoms:
, the total
number of atoms:
![\includegraphics[width=12cm]{figures/colvars_diagram}](img264.png)