



Next: Computing the work of
Up: Biasing and analysis methods
Previous: Metadynamics
Contents
Index
Subsections
The harmonic biasing method may be used to enforce fixed or moving restraints,
including variants of Steered and Targeted MD. Within energy minimization
runs, it allows for restrained minimization, e.g. to calculate relaxed potential
energy surfaces. In the context of the Colvars module,
harmonic potentials are meant according to their textbook definition:
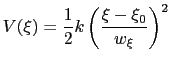 |
(13.34) |
There are two noteworthy aspects of this expression:
- Because the standard coefficient of
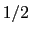 of the harmonic potential is included, this expression differs from harmonic bond and angle potentials historically used in common force fields, where the factor was typically omitted resulting in a non-standard definition of the force constant.
of the harmonic potential is included, this expression differs from harmonic bond and angle potentials historically used in common force fields, where the factor was typically omitted resulting in a non-standard definition of the force constant.
- The variable
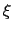 is not only centered at
is not only centered at 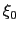 , but is also scaled by its characteristic length scale
, but is also scaled by its characteristic length scale 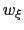 (keyword width).
The resulting dimensionless variable
(keyword width).
The resulting dimensionless variable
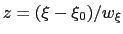 is typically easier to treat numerically: for example, when the forces typically experienced by
is typically easier to treat numerically: for example, when the forces typically experienced by 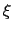 are much smaller than
are much smaller than 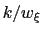 and
and 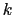 is chosen equal to
is chosen equal to
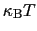 (thermal energy), the resulting probability distribution of
(thermal energy), the resulting probability distribution of 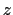 is approximately a Gaussian with mean equal to 0 and standard deviation equal to 1.
is approximately a Gaussian with mean equal to 0 and standard deviation equal to 1.
This property can be used for setting the force constant in umbrella-sampling ensemble runs: if the restraint centers are chosen in increments of 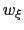 , the resulting distributions of
, the resulting distributions of 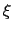 are most often optimally overlapped.
In regions where the underlying free-energy landscape induces highly skewed distributions of
are most often optimally overlapped.
In regions where the underlying free-energy landscape induces highly skewed distributions of 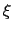 , additional windows may be added as needed, with spacings finer than
, additional windows may be added as needed, with spacings finer than 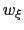 .
.
Beyond one dimension, the use of a scaled harmonic potential also allows a standard definition of a multi-dimensional restraint with a unified force constant:
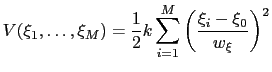 |
(13.35) |
If one-dimensional or homogeneous multi-dimensional restraints are defined, and there are no other uses for the parameter 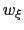 , width can be left at its default value of
, width can be left at its default value of 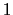 .
.
A harmonic restraint is defined by a harmonic {...} block, which may contain the following keywords:
-
name: see definition of name (biasing and analysis methods)
-
colvars: see definition of colvars (biasing and analysis methods)
-
outputEnergy: see definition of outputEnergy (biasing and analysis methods)
-
writeTIPMF: see definition of writeTIPMF (biasing and analysis methods)
-
writeTISamples: see definition of writeTISamples (biasing and analysis methods)
-
stepZeroData: see definition of stepZeroData (biasing and analysis methods)
-
forceConstant
 Scaled force constant (kcal/mol)
Scaled force constant (kcal/mol)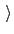
Context: harmonic
Acceptable values: positive decimal
Default value: 1.0
Description: This option defines a scaled force constant 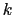 for the harmonic potential (eq. 13.36).
To ensure consistency for multidimensional restraints, it is divided internally by the square of the specific width of each variable (which is 1 by default).
This makes all values effectively dimensionless and of commensurate size.
For instance, if this force constant is set to the thermal energy
for the harmonic potential (eq. 13.36).
To ensure consistency for multidimensional restraints, it is divided internally by the square of the specific width of each variable (which is 1 by default).
This makes all values effectively dimensionless and of commensurate size.
For instance, if this force constant is set to the thermal energy
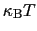 (equal to
(equal to 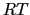 if molar units are used), then the amplitude of the thermal fluctuations of each variable
if molar units are used), then the amplitude of the thermal fluctuations of each variable 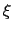 will be on the order of its width,
will be on the order of its width, 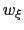 .
This can be used to estimate the optimal spacing of umbrella-sampling windows (under the assumption that the force constant is larger than the curvature of the underlying free energy).
The values of the actual force constants
.
This can be used to estimate the optimal spacing of umbrella-sampling windows (under the assumption that the force constant is larger than the curvature of the underlying free energy).
The values of the actual force constants
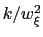 are always printed when the restraint is defined.
are always printed when the restraint is defined.
-
centers
 Initial harmonic restraint centers
Initial harmonic restraint centers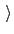
Context: harmonic
Acceptable values: space-separated list of colvar values
Description: The centers (equilibrium values) of the restraint, 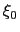 , are entered here.
The number of values must be the number of requested colvars.
Each value is a decimal number if the corresponding colvar returns
a scalar, a ``(x, y, z)'' triplet if it returns a unit
vector or a vector, and a ``(q0, q1, q2, q3)'' quadruplet
if it returns a rotational quaternion. If a colvar has
periodicities or symmetries, its closest image to the restraint
center is considered when calculating the harmonic potential.
, are entered here.
The number of values must be the number of requested colvars.
Each value is a decimal number if the corresponding colvar returns
a scalar, a ``(x, y, z)'' triplet if it returns a unit
vector or a vector, and a ``(q0, q1, q2, q3)'' quadruplet
if it returns a rotational quaternion. If a colvar has
periodicities or symmetries, its closest image to the restraint
center is considered when calculating the harmonic potential.
Tip: A complex set of restraints can be applied to a system,
by defining several colvars, and applying one or more harmonic
restraints to different groups of colvars. In some cases, dozens of
colvars can be defined, but their value may not be relevant: to
limit the size of the colvars trajectory file, it
may be wise to disable outputValue for such ``ancillary''
variables, and leave it enabled only for ``relevant'' ones.
The following options allow to change gradually the centers of the harmonic restraints during a simulations.
When the centers are changed continuously, a steered MD in a collective variable space is carried out.
-
targetCenters
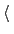 Steer the restraint centers towards these
targets
Steer the restraint centers towards these
targets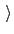
Context: harmonic
Acceptable values: space-separated list of colvar values
Description: When defined, the current centers will be moved towards
these values during the simulation.
By default, the centers are moved over a total of
targetNumSteps steps by a linear interpolation, in the
spirit of Steered MD.
If targetNumStages is set to a nonzero value, the
change is performed in discrete stages, lasting targetNumSteps
steps each. This second mode may be used to sample successive
windows in the context
of an Umbrella Sampling simulation.
When continuing a simulation
run, the centers specified in the configuration file
 colvarsConfig
colvarsConfig are overridden by those saved in
the restart file
are overridden by those saved in
the restart file  colvarsInput
colvarsInput .
To perform Steered MD in an arbitrary space of colvars, it is sufficient
to use this option and enable outputAccumulatedWork and/or
outputAppliedForce within each of the colvars involved.
.
To perform Steered MD in an arbitrary space of colvars, it is sufficient
to use this option and enable outputAccumulatedWork and/or
outputAppliedForce within each of the colvars involved.
-
targetNumSteps
 Number of steps for steering
Number of steps for steering
Context: harmonic
Acceptable values: positive integer
Description: In single-stage (continuous) transformations, defines the number of MD
steps required to move the restraint centers (or force constant)
towards the values specified with targetCenters or
targetForceConstant.
After the target values have been reached, the centers (resp. force
constant) are kept fixed. In multi-stage transformations, this sets the
number of MD steps per stage.
-
outputCenters
 Write the current centers to the trajectory file
Write the current centers to the trajectory file
Context: harmonic
Acceptable values: boolean
Default value: off
Description: If this option is chosen and colvarsTrajFrequency is not zero, the positions of the restraint centers will be written to the trajectory file during the simulation.
This option allows to conveniently extract the PMF from the colvars trajectory files in a steered MD calculation.
Note on restarting moving restraint simulations: Information
about the current step and stage of a simulation with moving restraints
is stored in the restart file (state file). Thus, such simulations can
be run in several chunks, and restarted directly using the same colvars
configuration file. In case of a restart, the values of parameters such
as targetCenters, targetNumSteps, etc. should not be
changed manually.
The centers of the harmonic restraints can also be changed in discrete stages: in this cases a one-dimensional umbrella sampling simulation is performed.
The sampling windows in simulation are calculated in sequence.
The colvars trajectory file may then be used both to evaluate the correlation times between consecutive windows, and to calculate the frequency distribution of the colvar of interest in each window.
Furthermore, frequency distributions on a predefined grid can be automatically obtained by using the histogram bias (see ![[*]](crossref.png) ).
).
To activate an umbrella sampling simulation, the same keywords as in the previous section can be used, with the addition of the following:
The force constant of the harmonic restraint may also be changed to equilibrate [76].
-
targetForceConstant
 Change the force constant towards this value
Change the force constant towards this value
Context: harmonic
Acceptable values: positive decimal
Description: When defined, the current forceConstant will be moved towards
this value during the simulation. Time evolution of the force constant
is dictated by the targetForceExponent parameter (see below).
By default, the force constant is changed smoothly over a total of
targetNumSteps steps. This is useful to introduce or
remove restraints in a progressive manner.
If targetNumStages is set to a nonzero value, the
change is performed in discrete stages, lasting targetNumSteps
steps each. This second mode may be used to compute the
conformational free energy change associated with the restraint, within
the FEP or TI formalisms. For convenience, the code provides an estimate
of the free energy derivative for use in TI. A more complete free energy
calculation (particularly with regard to convergence analysis),
while not handled by the Colvars module, can be performed by post-processing
the colvars trajectory, if colvarsTrajFrequency is set to a
suitably small value. It should be noted, however, that restraint
free energy calculations may be handled more efficiently by an
indirect route, through the
determination of a PMF for the restrained coordinate.[76]
-
targetForceExponent
 Exponent in the time-dependence of the force constant
Exponent in the time-dependence of the force constant
Context: harmonic
Acceptable values: decimal equal to or greater than 1.0
Default value: 1.0
Description: Sets the exponent, 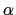 , in the function used to vary the force
constant as a function of time. The force is varied according to a
coupling parameter
, in the function used to vary the force
constant as a function of time. The force is varied according to a
coupling parameter 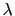 , raised to the power
, raised to the power 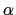 :
:
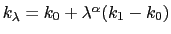 , where
, where 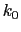 ,
,
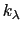 , and
, and 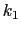 are the initial, current, and final values
of the force constant. The parameter
are the initial, current, and final values
of the force constant. The parameter 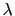 evolves linearly from
0 to 1, either smoothly, or in targetNumStages equally spaced
discrete stages, or according to an arbitrary schedule set with
lambdaSchedule.
When the initial value of the force constant is zero,
an exponent greater than 1.0 distributes the effects of introducing the
restraint more smoothly over time than a linear dependence, and
ensures that there is no singularity in the derivative of the
restraint free energy with respect to lambda. A value of 4 has
been found to give good results in some tests.
evolves linearly from
0 to 1, either smoothly, or in targetNumStages equally spaced
discrete stages, or according to an arbitrary schedule set with
lambdaSchedule.
When the initial value of the force constant is zero,
an exponent greater than 1.0 distributes the effects of introducing the
restraint more smoothly over time than a linear dependence, and
ensures that there is no singularity in the derivative of the
restraint free energy with respect to lambda. A value of 4 has
been found to give good results in some tests.
-
targetEquilSteps
 Number of steps discarded from TI estimate
Number of steps discarded from TI estimate
Context: harmonic
Acceptable values: positive integer
Description: Defines the number of steps within each stage that are considered
equilibration and discarded from the restraint free energy derivative
estimate reported reported in the output.
-
lambdaSchedule
 Schedule of lambda-points for changing force constant
Schedule of lambda-points for changing force constant
Context: harmonic
Acceptable values: list of real numbers between 0 and 1
Description: If specified together with targetForceConstant, sets the sequence of
discrete 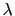 values that will be used for different stages.
values that will be used for different stages.




Next: Computing the work of
Up: Biasing and analysis methods
Previous: Metadynamics
Contents
Index
vmd@ks.uiuc.edu
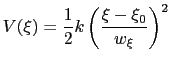
![]() , the resulting distributions of
, the resulting distributions of ![]() are most often optimally overlapped.
In regions where the underlying free-energy landscape induces highly skewed distributions of
are most often optimally overlapped.
In regions where the underlying free-energy landscape induces highly skewed distributions of ![]() , additional windows may be added as needed, with spacings finer than
, additional windows may be added as needed, with spacings finer than ![]() .
.
![]() , width can be left at its default value of
, width can be left at its default value of ![]() .
.
![[*]](crossref.png) ).
).