



Next: Trajectory output
Up: Defining collective variables
Previous: Scripted functions
Contents
Index
Subsections
Many algorithms require the definition of boundaries and/or characteristic spacings that can be used to define discrete ``states'' in the collective variable, or to combine variables with very different units.
The parameters described below offer a way to specify these parameters only once for each variable, while using them multiple times in restraints, time-dependent biases or analysis methods.
-
width
 Unit of the variable, or grid spacing
Unit of the variable, or grid spacing
Context: colvar
Acceptable values: positive decimal
Default value: 1.0
Description: This number defines the effective unit of measurement for the collective variable, and is used by the biasing methods for the following purposes.
Harmonic (![[*]](crossref.png) ), harmonic walls (
), harmonic walls (![[*]](crossref.png) ) and linear restraints (
) and linear restraints (![[*]](crossref.png) ) use it to set the physical unit of the force constant, which is useful for multidimensional restraints involving multiple variables with very different units (for examples,
) use it to set the physical unit of the force constant, which is useful for multidimensional restraints involving multiple variables with very different units (for examples,  or degrees
or degrees  ) with a single, scaled force constant.
The values of the scaled force constant in the units of each variable are printed at initialization time.
Histograms (
) with a single, scaled force constant.
The values of the scaled force constant in the units of each variable are printed at initialization time.
Histograms (![[*]](crossref.png) ), ABF (
), ABF (![[*]](crossref.png) ) and metadynamics (
) and metadynamics (![[*]](crossref.png) ) all use this number as the initial choice for the grid spacing along this variable: for this reason, width should generally be no larger than the standard deviation of the colvar in an unbiased simulation.
Unless it is required to control the spacing, it is usually simplest to keep the default value of 1, so that restraint force constants are provided with their full physical unit.
) all use this number as the initial choice for the grid spacing along this variable: for this reason, width should generally be no larger than the standard deviation of the colvar in an unbiased simulation.
Unless it is required to control the spacing, it is usually simplest to keep the default value of 1, so that restraint force constants are provided with their full physical unit.
-
lowerBoundary
 Lower boundary of the colvar
Lower boundary of the colvar
Context: colvar
Acceptable values: decimal
Default value: natural boundary of the function
Description: Defines the lowest end of the interval of ``relevant'' values for the variable.
This number can be, for example, a true physical boundary imposed by the choice of function (e.g. the distance function is always larger than zero): if this is the case, and only one function is used to define the variable, the default value of this number is set to the lowest end of the range of values of that function, if available (see Section ![[*]](crossref.png) ).
Alternatively, this value may be provided by the user, to represent for example the left-most point of a PMF calculation along this variable.
In the latter case, it is the user's responsibility to either (a) ensure the variable does not go significantly beyond the boundary (for example by adding a harmonicWalls restraint,
).
Alternatively, this value may be provided by the user, to represent for example the left-most point of a PMF calculation along this variable.
In the latter case, it is the user's responsibility to either (a) ensure the variable does not go significantly beyond the boundary (for example by adding a harmonicWalls restraint, ![[*]](crossref.png) ), or (b) instruct the code that this is a true physical boundary by setting hardLowerBoundary.
), or (b) instruct the code that this is a true physical boundary by setting hardLowerBoundary.
-
upperBoundary
 Upper boundary of the colvar
Upper boundary of the colvar
Context: colvar
Acceptable values: decimal
Default value: natural boundary of the function
Description: Similarly to lowerBoundary, defines the highest of the ``relevant'' values of the variable.
-
hardLowerBoundary
 Whether the lower boundary is the physical lower limit
Whether the lower boundary is the physical lower limit
Context: colvar
Acceptable values: boolean
Default value: provided by the component
Description: When the colvar has a ``natural'' boundary (for example, a distance colvar cannot go below 0) this flag is automatically enabled.
For more complex variable definitions, or when lowerBoundary is provided directly by the user, it may be useful to set this flag explicitly.
This option does not affect simulation results, but enables some internal optimizations by letting the code know that the variable is unable to cross the lower boundary, regardless of whether restraints are applied to it.
-
hardUpperBoundary
 Whether the upper boundary is the physical upper limit of the colvar's values
Whether the upper boundary is the physical upper limit of the colvar's values
Context: colvar
Acceptable values: boolean
Default value: provided by the component
Description: Analogous to hardLowerBoundary.
-
expandBoundaries
 Allow to expand the two boundaries if needed
Allow to expand the two boundaries if needed
Context: colvar
Acceptable values: boolean
Default value: off
Description: If defined, lowerBoundary and upperBoundary may be automatically expanded to accommodate colvar values that do not fit in the initial range.
Currently, this option is used by the metadynamics bias
(![[*]](crossref.png) ) to keep all of its hills fully within
the grid. This option cannot be used when
the initial boundaries already span the full period of a periodic
colvar.
) to keep all of its hills fully within
the grid. This option cannot be used when
the initial boundaries already span the full period of a periodic
colvar.
Many simulation methods and analysis tools write files that contain functions of the collective variables tabulated on a grid (e.g. potentials of mean force or multidimentional histograms) for the purpose of analyzing results.
Such files are produced by ABF (![[*]](crossref.png) ), metadynamics (
), metadynamics (![[*]](crossref.png) ), multidimensional histograms (
), multidimensional histograms (![[*]](crossref.png) ), as well as any restraint with optional thermodynamic integration support (
), as well as any restraint with optional thermodynamic integration support (![[*]](crossref.png) ).
).
In some cases, these files may also be read as input of a new simulation.
Suitable input files for this purpose are typically generated as output files of previous simulations, or directly by the user in the specific case of ensemble-biased metadynamics (![[*]](crossref.png) ).
This section explains the ``multicolumn'' format used by these files.
For a multidimensional function
).
This section explains the ``multicolumn'' format used by these files.
For a multidimensional function 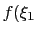 ,
, 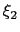 , ...
, ... the multicolumn grid format is defined as follows:
the multicolumn grid format is defined as follows:
| # |
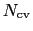
|
|
|
|
|
|
| # |
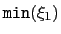
|

|
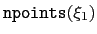
|
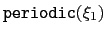
|
|
|
| # |
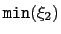
|

|
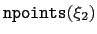
|
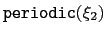
|
|
|
| # |
... |
... |
... |
... |
|
|
| # |
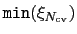
|

|
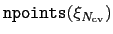
|
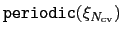
|
|
|
| |
|
|
|
|
|
|
| |
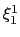
|
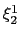
|
... |
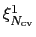
|
f(
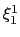 ,
,
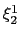 , ...,
, ...,
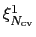 )
) |
|
| |
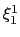
|
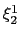
|
... |
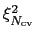
|
f(
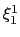 ,
,
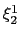 , ...,
, ...,
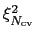 )
) |
|
| |
... |
... |
... |
... |
... |
|
| |
|
|
|
|
|
|
Lines beginning with the character ``#'' are the header of the file.
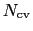 is the number of collective variables sampled by the grid.
For each variable
is the number of collective variables sampled by the grid.
For each variable 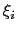 ,
,
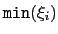 is the lowest value sampled by the grid (i.e. the left-most boundary of the grid along
is the lowest value sampled by the grid (i.e. the left-most boundary of the grid along 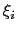 ),
),
 is the width of each grid step along
is the width of each grid step along 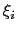 ,
,
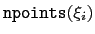 is the number of points and
is the number of points and
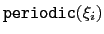 is a flag whose value is 1 or 0 depending on whether the grid is periodic along
is a flag whose value is 1 or 0 depending on whether the grid is periodic along 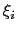 .
In most situations:
.
In most situations:
-
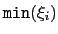 is given by the lowerBoundary keyword of the variable
is given by the lowerBoundary keyword of the variable 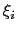 ;
;
-
 is given by the width keyword;
is given by the width keyword;
-
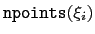 is calculated from the two above numbers and the upperBoundary keyword;
is calculated from the two above numbers and the upperBoundary keyword;
-
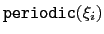 is set to 1 if and only if
is set to 1 if and only if 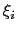 is periodic and the grids' boundaries cover its period.
is periodic and the grids' boundaries cover its period.
Exception: there is a slightly different header in PMF files computed by ABF (![[*]](crossref.png) ) or by other biases with an optional thermodynamic integration (TI) estimator (
) or by other biases with an optional thermodynamic integration (TI) estimator (![[*]](crossref.png) ).
In this case, free-energy gradients are accumulated on an (npoints)-long grid along each variable
).
In this case, free-energy gradients are accumulated on an (npoints)-long grid along each variable 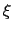 : after these gradients are integrated, the resulting PMF is discretized on a grid with (npoints+1) points along
: after these gradients are integrated, the resulting PMF is discretized on a grid with (npoints+1) points along 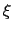 .
Therefore, the edges of the PMF's grid extend
.
Therefore, the edges of the PMF's grid extend
 above and below the original boundaries (unless these are periodic). The format of the file's header is otherwise unchanged.
above and below the original boundaries (unless these are periodic). The format of the file's header is otherwise unchanged.
After the header, the rest of the file contains values of the tabulated function
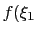 ,
, 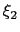 , ...
, ...
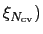 , one for each line.
The first
, one for each line.
The first
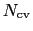 columns contain values of
columns contain values of 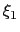 ,
, 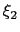 , ...
, ...
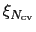 and the last column contains the value of the function
and the last column contains the value of the function 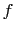 .
Points are sorted in ascending order with the fastest-changing values at the right (``C-style'' order).
Each sweep of the right-most variable
.
Points are sorted in ascending order with the fastest-changing values at the right (``C-style'' order).
Each sweep of the right-most variable
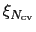 is terminated by an empty line.
For two dimensional grid files, this allows quick visualization by programs such as GNUplot.
is terminated by an empty line.
For two dimensional grid files, this allows quick visualization by programs such as GNUplot.
Example 1: multicolumn text file for a one-dimensional histogram with lowerBoundary = 15, upperBoundary = 48 and width = 0.1.
| # |
1 |
|
|
|
|
| # |
15 |
0.1 |
330 |
0 |
|
| |
|
|
|
|
|
| |
15.05 |
6.14012e-07 |
|
|
|
| |
15.15 |
7.47644e-07 |
|
|
|
| |
... |
... |
|
|
|
| |
47.85 |
1.65944e-06 |
|
|
|
| |
47.95 |
1.46712e-06 |
|
|
|
| |
|
|
|
|
|
Example 2: multicolumn text file for a two-dimensional histogram of two dihedral angles (periodic interval with 6 bins):
bins):
| |
|
|
|
|
|
| # |
2 |
|
|
|
|
| # |
-180.0 |
6.0 |
30 |
1 |
|
| # |
-180.0 |
6.0 |
30 |
1 |
|
| |
|
|
|
|
|
| |
-177.0 |
-177.0 |
8.97117e-06 |
|
|
| |
-177.0 |
-171.0 |
1.53525e-06 |
|
|
| |
... |
... |
... |
|
|
| |
-177.0 |
177.0 |
2.442956-06 |
|
|
| |
|
|
|
|
|
| |
-171.0 |
-177.0 |
2.04702e-05 |
|
|
| |
... |
... |
... |
|
|




Next: Trajectory output
Up: Defining collective variables
Previous: Scripted functions
Contents
Index
vmd@ks.uiuc.edu
![[*]](crossref.png) ), harmonic walls (
), harmonic walls (![[*]](crossref.png) ) and linear restraints (
) and linear restraints (![[*]](crossref.png) ) use it to set the physical unit of the force constant, which is useful for multidimensional restraints involving multiple variables with very different units (for examples,
) use it to set the physical unit of the force constant, which is useful for multidimensional restraints involving multiple variables with very different units (for examples, ![[*]](crossref.png) ), ABF (
), ABF (![[*]](crossref.png) ) and metadynamics (
) and metadynamics (![[*]](crossref.png) ) all use this number as the initial choice for the grid spacing along this variable: for this reason, width should generally be no larger than the standard deviation of the colvar in an unbiased simulation.
Unless it is required to control the spacing, it is usually simplest to keep the default value of 1, so that restraint force constants are provided with their full physical unit.
) all use this number as the initial choice for the grid spacing along this variable: for this reason, width should generally be no larger than the standard deviation of the colvar in an unbiased simulation.
Unless it is required to control the spacing, it is usually simplest to keep the default value of 1, so that restraint force constants are provided with their full physical unit.
![[*]](crossref.png) ).
Alternatively, this value may be provided by the user, to represent for example the left-most point of a PMF calculation along this variable.
In the latter case, it is the user's responsibility to either (a) ensure the variable does not go significantly beyond the boundary (for example by adding a harmonicWalls restraint,
).
Alternatively, this value may be provided by the user, to represent for example the left-most point of a PMF calculation along this variable.
In the latter case, it is the user's responsibility to either (a) ensure the variable does not go significantly beyond the boundary (for example by adding a harmonicWalls restraint, ![[*]](crossref.png) ), or (b) instruct the code that this is a true physical boundary by setting hardLowerBoundary.
), or (b) instruct the code that this is a true physical boundary by setting hardLowerBoundary.
![[*]](crossref.png) ) to keep all of its hills fully within
the grid. This option cannot be used when
the initial boundaries already span the full period of a periodic
colvar.
) to keep all of its hills fully within
the grid. This option cannot be used when
the initial boundaries already span the full period of a periodic
colvar.