The block alpha {...} defines the
parameters to calculate the helical content of a segment of protein
residues. The ![]() -helical content across the
-helical content across the ![]() residues
residues
![]() to
to ![]() is calculated by the formula:
is calculated by the formula:
List of keywords (see also ![[*]](crossref.png) for additional options):
for additional options):
This component returns positive values, always comprised between 0
(lowest ![]() -helical score) and 1 (highest
-helical score) and 1 (highest ![]() -helical
score).
-helical
score).
The block dihedralPC {...} defines the
parameters to calculate the projection of backbone dihedral angles within
a protein segment onto a dihedral principal component, following
the formalism of dihedral principal component analysis (dPCA) proposed by
Mu et al.[51] and documented in detail by Altis et
al.[52].
Given a peptide or protein segment of ![]() residues, each with Ramachandran
angles
residues, each with Ramachandran
angles ![]() and
and ![]() , dPCA rests on a variance/covariance analysis
of the
, dPCA rests on a variance/covariance analysis
of the ![]() variables
variables
![]() . Note that angles
. Note that angles ![]() and
and ![]() have little impact on chain conformation, and are therefore discarded,
following the implementation of dPCA in the analysis software Carma.[53]
have little impact on chain conformation, and are therefore discarded,
following the implementation of dPCA in the analysis software Carma.[53]
For a given principal component (eigenvector) of coefficients
![]() ,
the projection of the current backbone conformation is:
,
the projection of the current backbone conformation is:
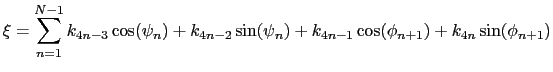 |
(13.12) |
dihedralPC expects the same parameters as the alpha component for defining the relevant residues (residueRange and psfSegID) in addition to the following:
List of keywords (see also ![[*]](crossref.png) for additional options):
for additional options):