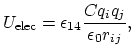



Next: Non-bonded interactions
Up: Force Field Parameters
Previous: Force Field Parameters
Contents
Index
Subsections
Evaluating the force is the most computationally demanding
part of molecular dynamics.
The force is the negative gradient of a scalar potential energy function,
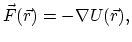 |
(1) |
and, for systems of biomolecules,
this potential function involves the summing,
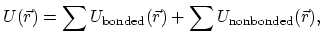 |
(2) |
over a large number of bonded and nonbonded terms.
The bonded potential terms involve 2-, 3-, and 4-body interactions
of covalently bonded atoms,
with 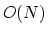 terms in the summation.
The nonbonded potential terms involve interactions
between all pairs of atoms
(usually excluding pairs of atoms already involved in a bonded term),
with
terms in the summation.
The nonbonded potential terms involve interactions
between all pairs of atoms
(usually excluding pairs of atoms already involved in a bonded term),
with 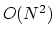 terms in the summation,
although fast evaluation techniques are used to
compute good approximations to their contribution to the potential
with
terms in the summation,
although fast evaluation techniques are used to
compute good approximations to their contribution to the potential
with 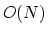 or
or
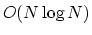 computational cost.
computational cost.
The bonded potential terms involve 2-, 3-, and 4-body interactions
of covalently bonded atoms.
The 2-body spring bond potential
describes the harmonic vibrational motion
between an 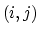 -pair of covalently bonded atoms,
-pair of covalently bonded atoms,
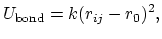 |
(3) |
where
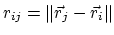 gives the distance
between the atoms,
gives the distance
between the atoms,
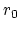 is the equilibrium distance,
and
is the equilibrium distance,
and 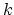 is the spring constant.
is the spring constant.
The 3-body angular bond potential
describes the angular vibrational motion
occurring between an 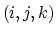 -triple of covalently bonded atoms,
-triple of covalently bonded atoms,
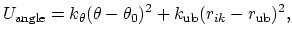 |
(4) |
where, in the first term,
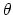 is the angle in radians between vectors
is the angle in radians between vectors
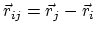 and
and
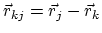 ,
,
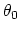 is the equilibrium angle,
and
is the equilibrium angle,
and
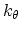 is the angle constant.
The second term is the Urey-Bradley term
used to describe a
(noncovalent) spring between the outer
is the angle constant.
The second term is the Urey-Bradley term
used to describe a
(noncovalent) spring between the outer 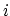 and
and 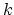 atoms,
active when constant
atoms,
active when constant
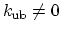 ,
where, like the spring bond,
,
where, like the spring bond,
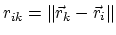 gives the distance between
the pair of atoms and
gives the distance between
the pair of atoms and
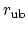 is the equilibrium distance.
is the equilibrium distance.
The 4-body torsion angle (also known as dihedral angle) potential
describes the angular spring between the planes formed
by the first three and last three atoms of
a consecutively bonded 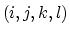 -quadruple of atoms,
-quadruple of atoms,
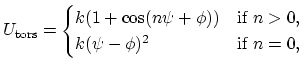 |
(5) |
where 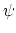 is the angle in radians between
the
is the angle in radians between
the 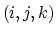 -plane and the
-plane and the 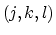 -plane.
The integer constant
-plane.
The integer constant 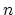 is nonnegative and indicates the periodicity.
For
is nonnegative and indicates the periodicity.
For 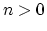 ,
, 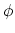 is the phase shift angle
and
is the phase shift angle
and 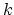 is the multiplicative constant.
For
is the multiplicative constant.
For 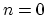 ,
, 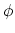 acts as an equilibrium angle
and the units of
acts as an equilibrium angle
and the units of 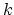 change to
potential
change to
potential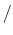 rad
rad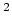 .
A given
.
A given 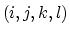 -quadruple of atoms might contribute
multiple terms to the potential,
each with its own parameterization.
The use of multiple terms for a torsion angle allows for
complex angular variation of the potential,
effectively a truncated Fourier series.
-quadruple of atoms might contribute
multiple terms to the potential,
each with its own parameterization.
The use of multiple terms for a torsion angle allows for
complex angular variation of the potential,
effectively a truncated Fourier series.
The nonbonded potential terms involve interactions
between all 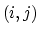 -pairs of atoms,
usually excluding pairs of atoms already involved in a bonded term.
Even using a fast evaluation methods
the cost of computing the nonbonded potentials dominates the work
required for each time step of an MD simulation.
-pairs of atoms,
usually excluding pairs of atoms already involved in a bonded term.
Even using a fast evaluation methods
the cost of computing the nonbonded potentials dominates the work
required for each time step of an MD simulation.
The Lennard-Jones potential
accounts for the weak dipole attraction between distant atoms and
the hard core repulsion as atoms become close,
![$\displaystyle U_{\text{LJ}} = (-E_{\text{min}}) \left[ \left( \frac{R_{\text{mi...
...ij}} \right)^{12} - 2 \left( \frac{R_{\text{min}}}{r_{ij}} \right)^{6} \right],$](img56.png) |
(6) |
where
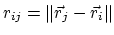 gives the distance
between the pair of atoms.
The parameter
gives the distance
between the pair of atoms.
The parameter
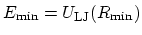 is
the minimum of the potential term
(
is
the minimum of the potential term
(
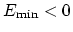 , which means that
, which means that
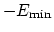 is the well-depth).
The Lennard-Jones potential approaches 0 rapidly as
is the well-depth).
The Lennard-Jones potential approaches 0 rapidly as 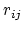 increases, so it is usually truncated (smoothly shifted) to 0
past a cutoff radius, requiring
increases, so it is usually truncated (smoothly shifted) to 0
past a cutoff radius, requiring 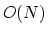 computational cost.
computational cost.
The electrostatic potential
is repulsive for atomic charges with the same sign
and attractive for atomic charges with opposite signs,
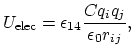 |
(7) |
where
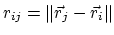 gives the distance
between the pair of atoms,
and
gives the distance
between the pair of atoms,
and 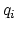 and
and 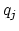 are the charges on the respective atoms.
Coulomb's constant
are the charges on the respective atoms.
Coulomb's constant 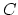 and the dielectric constant
and the dielectric constant
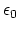 are fixed for all electrostatic interactions.
The parameter
are fixed for all electrostatic interactions.
The parameter
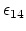 is a unitless scaling factor
whose value is 1,
except for a modified 1-4 interaction,
where the pair of atoms is separated by a sequence
of three covalent bonds (so that the atoms might
also be involved in a torsion angle interaction),
in which case
is a unitless scaling factor
whose value is 1,
except for a modified 1-4 interaction,
where the pair of atoms is separated by a sequence
of three covalent bonds (so that the atoms might
also be involved in a torsion angle interaction),
in which case
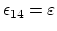 ,
for a fixed constant
,
for a fixed constant
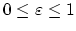 .
Although the electrostatic potential may be computed with
a cutoff like the Lennard-Jones potential,
the
.
Although the electrostatic potential may be computed with
a cutoff like the Lennard-Jones potential,
the 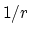 potential approaches 0 much more
slowly than the
potential approaches 0 much more
slowly than the 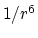 potential,
so neglecting the long range electrostatic terms
can degrade qualitative results,
especially for highly charged systems.
There are other fast evaluation methods that approximate
the contribution to the long range electrostatic terms
that require
potential,
so neglecting the long range electrostatic terms
can degrade qualitative results,
especially for highly charged systems.
There are other fast evaluation methods that approximate
the contribution to the long range electrostatic terms
that require 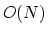 or
or
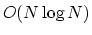 computational cost,
depending on the method.
computational cost,
depending on the method.




Next: Non-bonded interactions
Up: Force Field Parameters
Previous: Force Field Parameters
Contents
Index
http://www.ks.uiuc.edu/Research/namd/
![]() -pair of covalently bonded atoms,
-pair of covalently bonded atoms,
![]() -triple of covalently bonded atoms,
-triple of covalently bonded atoms,
![]() -quadruple of atoms,
-quadruple of atoms,
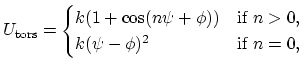
![]() -pairs of atoms,
usually excluding pairs of atoms already involved in a bonded term.
Even using a fast evaluation methods
the cost of computing the nonbonded potentials dominates the work
required for each time step of an MD simulation.
-pairs of atoms,
usually excluding pairs of atoms already involved in a bonded term.
Even using a fast evaluation methods
the cost of computing the nonbonded potentials dominates the work
required for each time step of an MD simulation.
![$\displaystyle U_{\text{LJ}} = (-E_{\text{min}}) \left[ \left( \frac{R_{\text{mi...
...ij}} \right)^{12} - 2 \left( \frac{R_{\text{min}}}{r_{ij}} \right)^{6} \right],$](img56.png)