



Next: Biasing and analysis methods
Up: Collective Variable-based Calculations (Colvars)
Previous: Defining collective variables
Contents
Index
Subsections
Selecting atoms
To define collective variables, atoms are usually selected as groups. Each group is defined using an identifier that is unique in the context of the specific colvar component (e.g. for a distance component, the two groups are group1 and group2).
The identifier is followed by a brace-delimited block containing selection keywords and other parameters, including an optional name:
- name
 Unique name for the atom group
Unique name for the atom group 
Context: atom group
Acceptable Values: string
Description: This parameter defines a unique name for this atom group, which can be referred to
in the definition of other atom groups (including in other colvars) by invoking
atomsOfGroup as a selection keyword.
Atom selection keywords
Selection keywords may be used individually or in combination with each other, and each can be repeated any number of times.
Selection is incremental: each keyword adds the corresponding atoms to the selection, so that different sets of atoms can be combined.
However, atoms included by multiple keywords are only counted once.
Below is an example configuration for an atom group called ``atoms''.
Note: this is an unusually varied combination of selection keywords, demonstrating how they can be combined together: most simulations only use one of them.
atoms {
# add atoms 1 and 3 to this group (note: the first atom in the system is 1)
atomNumbers {
1 3
}
# add atoms starting from 20 up to and including 50
atomNumbersRange 20-50
# add all the atoms with occupancy 2 in the file atoms.pdb
atomsFile atoms.pdb
atomsCol O
atomsColValue 2.0
# add all the C-alphas within residues 11 to 20 of segments "PR1" and "PR2"
psfSegID PR1 PR2
atomNameResidueRange CA 11-20
atomNameResidueRange CA 11-20
# add index group (requires a .ndx file to be provided globally)
indexGroup Water
}
The resulting selection includes atoms 1 and 3, those between 20 and 50, the
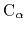 atoms between residues 11 and 20 of the two segments PR1 and PR2, and those in the index group called ``Water''.
The indices of this group are read from the file provided by the global keyword indexFile (see 9.2.5).
atoms between residues 11 and 20 of the two segments PR1 and PR2, and those in the index group called ``Water''.
The indices of this group are read from the file provided by the global keyword indexFile (see 9.2.5).
The complete list of selection keywords available in NAMD is:
- atomNumbers
 List of atom numbers
List of atom numbers 
Context: atom group
Acceptable Values: space-separated list of positive integers
Description: This option adds to the group all the atoms whose numbers are in
the list. The number of the first atom in the system is 1: to convert from a VMD selection, use ``atomselect get serial''.
- indexGroup
 Name of index group to be used (GROMACS format)
Name of index group to be used (GROMACS format) 
Context: atom group
Acceptable Values: string
Description: If the name of an index file has been provided by indexFile, this option allows to select one index group from that file: the atoms from that index group will be used to define the current group.
- atomsOfGroup
 Name of group defined previously
Name of group defined previously 
Context: atom group
Acceptable Values: string
Description: Refers to a group defined previously using its user-defined name.
This adds all atoms of that named group to the current group.
- atomNumbersRange
 Atoms within a number range
Atoms within a number range 
Context: atom group
Acceptable Values:  Starting number
Starting number -
- Ending number
Ending number
Description: This option includes in the group all atoms whose numbers are within the range specified. The number of the first atom in the system is 1.
- atomNameResidueRange
 Named atoms within a range of residue numbers
Named atoms within a range of residue numbers 
Context: atom group
Acceptable Values:  Atom name
Atom name
 Starting residue
Starting residue -
- Ending residue
Ending residue
Description: This option adds to the group all the atoms with the provided
name, within residues in the given range.
- psfSegID
 PSF segment identifier
PSF segment identifier 
Context: atom group
Acceptable Values: space-separated list of strings (max 4 characters)
Description: This option sets the PSF segment identifier for
atomNameResidueRange. Multiple values may be provided,
which correspond to multiple instances of
atomNameResidueRange, in order of their occurrence.
This option is only necessary if a PSF topology file is used.
- atomsFile
 PDB file name for atom selection
PDB file name for atom selection 
Context: atom group
Acceptable Values: UNIX filename
Description: This option selects atoms from the PDB file provided and adds them
to the group according to numerical flags in the column
atomsCol. Note: the sequence of atoms in the PDB file
provided must match that in the system's topology.
- atomsCol
 PDB column to use for atom selection flags
PDB column to use for atom selection flags 
Context: atom group
Acceptable Values: O, B, X, Y, or Z
Description: This option specifies which PDB column in atomsFile is used to determine which atoms are to be included in the group.
- atomsColValue
 Atom selection flag in the PDB column
Atom selection flag in the PDB column 
Context: atom group
Acceptable Values: positive decimal
Description: If defined, this value in atomsCol identifies atoms in atomsFile that are included in the group.
If undefined, all atoms with a non-zero value in atomsCol are included.
- dummyAtom
 Dummy atom position (Å)
Dummy atom position (Å) 
Context: atom group
Acceptable Values: (x, y, z) triplet
Description: Instead of selecting any atom, this option makes the group a virtual particle at a fixed position in space. This is useful e.g. to replace a group's center of geometry with a user-defined position.
Moving frame of reference.
The following options define an automatic calculation of an optimal translation (centerReference) or optimal rotation (rotateReference), that superimposes the positions of this group to a provided set of reference coordinates.
This can allow, for example, to effectively remove from certain colvars the effects of molecular tumbling and of diffusion.
Given the set of atomic positions
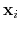 , the colvar
, the colvar 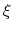 can be defined on a set of roto-translated positions
can be defined on a set of roto-translated positions
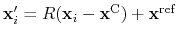 .
.
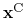 is the geometric center of the
is the geometric center of the
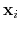 ,
, 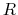 is the optimal rotation matrix to the reference positions and
is the optimal rotation matrix to the reference positions and
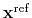 is the geometric center of the reference positions.
is the geometric center of the reference positions.
Components that are defined based on pairwise distances are naturally invariant under global roto-translations.
Other components are instead affected by global rotations or translations: however, they can be made invariant if they are expressed in the frame of reference of a chosen group of atoms, using the centerReference and rotateReference options.
Finally, a few components are defined by convention using a roto-translated frame (e.g. the minimal RMSD): for these components, centerReference and rotateReference are enabled by default.
In typical applications, the default settings result in the expected behavior.
rotateReference affects coordinates that depend on minimum-image distances in periodic boundary conditions (PBC).
After rotation of the coordinates, the periodic cell vectors become irrelevant: the rotated system is effectively non-periodic.
A safe way to handle this is to ensure that the relevant inter-group distance vectors remain smaller than the half-size of the periodic cell.
If this is not desirable, one should avoid the rotating frame of reference, and apply orientational restraints to the reference group instead, in order to keep the orientation of the reference group consistent with the orientation of the periodic cell.
Note that centerReference and rotateReference may affect the Jacobian derivative of colvar components in a way that is not taken into account by default.
Be careful when using these options in ABF simulations or when using total force values.
- centerReference
 Implicitly remove translations for this group
Implicitly remove translations for this group 
Context: atom group
Acceptable Values: boolean
Default Value: off
Description: If this option is on, the center of geometry of the group will be aligned with that of the reference positions provided by either refPositions or refPositionsFile.
Colvar components will only have access to the aligned positions.
Note: unless otherwise specified, rmsd and eigenvector set this option to on by default.
- rotateReference
 Implicitly remove rotations for this group
Implicitly remove rotations for this group 
Context: atom group
Acceptable Values: boolean
Default Value: off
Description: If this option is on, the coordinates of this group will be optimally superimposed to the reference positions provided by either refPositions or refPositionsFile.
The rotation will be performed around the center of geometry if centerReference is on, or around the origin otherwise.
The algorithm used is the same employed by the orientation colvar component [26].
Forces applied to the atoms of this group will also be implicitly rotated back to the original frame.
Note: unless otherwise specified, rmsd and eigenvector set this option to on by default.
- refPositions
 Reference positions for fitting (Å)
Reference positions for fitting (Å) 
Context: atom group
Acceptable Values: space-separated list of (x, y, z) triplets
Description: This option provides a list of reference coordinates for centerReference and/or rotateReference, and is mutually exclusive with refPositionsFile.
If only centerReference is on, the list may contain a single (x, y, z) triplet; if also rotateReference is on, the list should be as long as the atom group, and its order must match the order in which atoms were defined.
- refPositionsFile
 File containing the reference positions for fitting
File containing the reference positions for fitting 
Context: atom group
Acceptable Values: UNIX filename
Description: This option provides a list of reference coordinates for centerReference and/or rotateReference, and is mutually exclusive with refPositions.
The acceptable file format is XYZ, which is read in double precision, or PDB; the latter is discouraged if the precision of the reference coordinates is a concern.
Atomic positions are read differently depending on the following scenarios:
(i) the file contains exactly as many records as the atoms in the group: all positions are read in sequence;
(ii) (most common case) the file contains coordinates for the entire system: only the positions corresponding to the numeric indices of the atom group are read;
(iii) if the file is a PDB file and refPositionsCol is specified, positions are read according to the value of the column refPositionsCol (which may be the same as atomsCol).
In each case, atoms are read from the file in order of increasing number.
- refPositionsCol
 PDB column containing atom flags
PDB column containing atom flags 
Context: atom group
Acceptable Values: O, B, X, Y, or Z
Description: Like atomsCol for atomsFile, indicates which column to use to identify the atoms in refPositionsFile (if this is a PDB file).
- refPositionsColValue
 Atom selection flag in the PDB column
Atom selection flag in the PDB column 
Context: atom group
Acceptable Values: positive decimal
Description: Analogous to atomsColValue, but applied to refPositionsCol.
- fittingGroup
 Use an alternate set of atoms to define the roto-translation
Use an alternate set of atoms to define the roto-translation 
Context: atom group
Acceptable Values: Block fittingGroup { ... }
Default Value: This atom group itself
Description: If either centerReference or rotateReference is defined, this keyword defines an alternate atom group to calculate the optimal roto-translation.
Use this option to define a continuous rotation if the structure of the group involved changes significantly (a typical symptom would be the message ``Warning: discontinuous rotation!'').
The following example illustrates the use of fittingGroup as part of a Distance to Bound Configuration (DBC)
coordinate for use in ligand restraints for binding affinity calculations.[94]
The group called ``atoms'' describes coordinates of a ligand's atoms, expressed in a moving frame of
reference tied to a binding site (here within a protein).
An optimal roto-translation is calculated automatically by fitting the C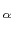 trace of the rest of the protein onto the coordinates provided by a PDB file.
To define a DBC coordinate, this atom group would be used within an rmsd (see 9.3.5) function.
trace of the rest of the protein onto the coordinates provided by a PDB file.
To define a DBC coordinate, this atom group would be used within an rmsd (see 9.3.5) function.
# Example: defining a group "atoms" (the ligand) whose coordinates are expressed
# in a roto-translated frame of reference defined by a second group (the receptor)
atoms {
atomNumbers 1 2 3 4 5 6 7 # atoms of the ligand (1-based)
centerReference yes
rotateReference yes
fittingGroup {
# define the frame by fitting alpha carbon atoms
# in 2 protein segments close to the site
psfSegID PROT PROT
atomNameResidueRange CA 1-40
atomNameResidueRange CA 59-100
}
refPositionsFile all.pdb # can be the entire system
}
The following two options have default values appropriate for the vast majority of applications, and are only provided to support rare, special cases.
Treatment of periodic boundary conditions.
In simulations with periodic boundary conditions, NAMD maintains
the coordinates of all the atoms within a molecule contiguous to
each other (i.e. there are no spurious ``jumps'' in the molecular
bonds). The Colvars module relies on this when calculating a group's
center of geometry, but this condition may fail if the group spans
different molecules. In that case, writing the NAMD output and restart files
using wrapAll or wrapWater could produce wrong results
when a simulation run is continued from a previous one.
The user should then determine, according to which
type of colvars are being calculated, whether wrapAll or
wrapWater can be enabled.
In general, internal coordinate wrapping by NAMD does not affect the calculation of colvars if each atom group satisfies one or more of the following:
- i)
- it is composed by only one atom;
- ii)
- it is used by a colvar component which does not make use of its center of geometry, but only of pairwise distances (distanceInv, coordNum, hBond, alpha, dihedralPC);
- iii)
- it is used by a colvar component that ignores the ill-defined Cartesian components of its center of mass (such as the
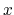 and
and 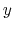 components of a membrane's center of mass modeled with distanceZ);
components of a membrane's center of mass modeled with distanceZ);
- iv)
- it has all of its atoms within the same molecular fragment.
Performance of a Colvars calculation based on group size.
In simulations performed with message-passing programs (such as NAMD or LAMMPS), the calculation of energy and forces is distributed (i.e., parallelized) across multiple nodes, as well as over the processor cores of each node.
When Colvars is enabled, certain atomic coordinates are collected on a single node, where the calculation of collective variables and of their biases is executed.
This means that for simulations over large numbers of nodes, a Colvars calculation may produce a significant overhead, coming from the costs of transmitting atomic coordinates to one node and of processing them.
The latency-tolerant design and dynamic load balancing of NAMD may alleviate both factors, but a noticeable performance impact may be observed.
Performance can be improved in multiple ways:
- The calculation of variables, components and biases can be distributed over the processor cores of the node where the Colvars module is executed.
Currently, an equal weight is assigned to each colvar, or to each component of those colvars that include more than one component.
The performance of simulations that use many colvars or components is improved automatically.
For simulations that use a single large colvar, it may be advisable to partition it in multiple components, which will be then distributed across the available cores.
In NAMD, this feature is enabled in all binaries compiled using SMP builds of Charm++ with the CkLoop extension.
If printed, the message ``SMP parallelism is available.'' indicates the availability of the option.
If available, the option is turned on by default, but may be disabled using the keyword smp (see 9.2.5) if required for debugging.
- NAMD also offers a parallelized calculation of the centers of mass of groups of atoms.
This option is on by default for all components that are simple functions of centers of mass, and is controlled by the keyword scalable (see 9.3.12).
When supported, the message ``Will enable scalable calculation for group ...'' is printed for each group.
- As a general rule, the size of atom groups should be kept relatively small (up to a few thousands of atoms, depending on the size of the entire system in comparison).
To gain an estimate of the computational cost of a large colvar, one can use a test calculation of the same colvar in VMD (hint: use the time Tcl command to measure the cost of running cv update).




Next: Biasing and analysis methods
Up: Collective Variable-based Calculations (Colvars)
Previous: Defining collective variables
Contents
Index
http://www.ks.uiuc.edu/Research/namd/