

Next: Sequence and structural alignments
Up: Bioinformatics Tutorial
Previous: SCOP fold classification
Subsections
Sequence Alignment Algorithms
In this section you will optimally align two short protein sequences using
pen and paper, then search for homologous proteins by using a
computer program to align several, much longer, sequences.
Dynamic programming algorithms are recursive algorithms modified to store
intermediate results, which improves efficiency for certain problems. The
Smith-Waterman (Needleman-Wunsch) algorithm uses a dynamic programming
algorithm to find the optimal local (global)
alignment of two sequences -- 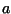 and
and 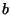 . The alignment algorithm is based on
finding the elements of a matrix
. The alignment algorithm is based on
finding the elements of a matrix 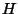 where the element
where the element 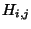 is the
optimal score for aligning the sequence (
is the
optimal score for aligning the sequence (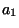 ,
,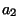 ,...,
,...,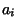 ) with
(
) with
(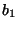 ,
,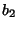 ,.....,
,.....,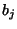 ). Two similar amino acids (e.g. arginine and lysine)
receive a high score, two dissimilar amino acids (e.g. arginine and glycine)
receive a low score. The higher the score of a path through the matrix, the better
the alignment. The matrix
). Two similar amino acids (e.g. arginine and lysine)
receive a high score, two dissimilar amino acids (e.g. arginine and glycine)
receive a low score. The higher the score of a path through the matrix, the better
the alignment. The matrix 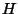 is found by progressively finding the matrix
elements, starting at
is found by progressively finding the matrix
elements, starting at 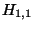 and proceeding in the directions of increasing
and proceeding in the directions of increasing
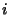 and
and 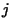 . Each element is set according to:
. Each element is set according to:
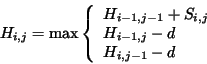
where 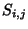 is the similarity score of comparing amino acid
is the similarity score of comparing amino acid 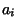 to amino
acid
to amino
acid 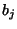 (obtained here from the BLOSUM40 similarity table) and
(obtained here from the BLOSUM40 similarity table) and 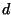 is the
penalty for a single gap. The matrix is initialized with
is the
penalty for a single gap. The matrix is initialized with 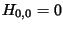 . When
obtaining the local Smith-Waterman alignment,
. When
obtaining the local Smith-Waterman alignment, 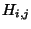 is modified:
is modified:
The gap penalty can be modified, for instance, 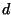 can be replaced by
can be replaced by
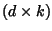 , where
, where 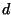 is the penalty for a single gap
and
is the penalty for a single gap
and 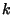 is the number of consecutive gaps.
is the number of consecutive gaps.
Once the optimal alignment score is found, the ``traceback'' through 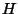 along
the optimal path is found, which corresponds to the the optimal sequence
alignment for the score. In the next set of exercises you will manually
implement the Needleman-Wunsch alignment for a pair of short sequences, then
perform global sequence alignments with a computer program developed by Anurag
Sethi, which is based on the Needleman-Wunsch algorithm with an affine gap
penalty,
along
the optimal path is found, which corresponds to the the optimal sequence
alignment for the score. In the next set of exercises you will manually
implement the Needleman-Wunsch alignment for a pair of short sequences, then
perform global sequence alignments with a computer program developed by Anurag
Sethi, which is based on the Needleman-Wunsch algorithm with an affine gap
penalty, 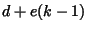 , where
, where 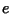 is the extension gap penalty. The output
file will be in the GCG format, one of the two standard formats in
bioinformatics for storing sequence information (the other standard format is
FASTA).
is the extension gap penalty. The output
file will be in the GCG format, one of the two standard formats in
bioinformatics for storing sequence information (the other standard format is
FASTA).
Manually perform a Needleman-Wunsch alignment
In the first exercise you will test the Smith-Waterman algorithm on a short
sequence parts of hemoglobin (PDB code 1AOW) and myoglobin 1 (PDB code 1AZI).
- Here you will align the sequence HGSAQVKGHG to the sequence KTEAEMKASEDLKKHGT.
- The two sequences are arranged in a matrix in Table 3.
The sequences start at the upper right corner, the initial gap penalties
are listed at each offset starting position. With each move from the start
position, the initial penalty increase by our single gap penalty of 8.
Table 3:
The empty matrix with initial gap penalties.
| |
|
H |
G |
S |
A |
Q |
V |
K |
G |
H |
G |
| |
0 |
-8 |
-16 |
-24 |
-32 |
-40 |
-48 |
-56 |
-64 |
-72 |
-80 |
| K |
-8 |
|
|
|
|
|
|
|
|
|
|
| T |
-16 |
|
|
|
|
|
|
|
|
|
|
| E |
-24 |
|
|
|
|
|
|
|
|
|
|
| A |
-32 |
|
|
|
|
|
|
|
|
|
|
| E |
-40 |
|
|
|
|
|
|
|
|
|
|
| M |
-48 |
|
|
|
|
|
|
|
|
|
|
| K |
-56 |
|
|
|
|
|
|
|
|
|
|
| A |
-64 |
|
|
|
|
|
|
|
|
|
|
| S |
-72 |
|
|
|
|
|
|
|
|
|
|
| E |
-80 |
|
|
|
|
|
|
|
|
|
|
| D |
-88 |
|
|
|
|
|
|
|
|
|
|
| L |
-96 |
|
|
|
|
|
|
|
|
|
|
| K |
-104 |
|
|
|
|
|
|
|
|
|
|
| K |
-112 |
|
|
|
|
|
|
|
|
|
|
| H |
-120 |
|
|
|
|
|
|
|
|
|
|
| G |
-128 |
|
|
|
|
|
|
|
|
|
|
| T |
-136 |
|
|
|
|
|
|
|
|
|
|
|
- The first step is to fill in the similarity scores S
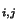 from looking up
the matches in the BLOSUM40 table, shown here labeled with 1-letter amino acid
codes:
from looking up
the matches in the BLOSUM40 table, shown here labeled with 1-letter amino acid
codes:
A 5
R -2 9
N -1 0 8
D -1 -1 2 9
C -2 -3 -2 -2 16
Q 0 2 1 -1 -4 8
E -1 -1 -1 2 -2 2 7
G 1 -3 0 -2 -3 -2 -3 8
H -2 0 1 0 -4 0 0 -2 13
I -1 -3 -2 -4 -4 -3 -4 -4 -3 6
L -2 -2 -3 -3 -2 -2 -2 -4 -2 2 6
K -1 3 0 0 -3 1 1 -2 -1 -3 -2 6
M -1 -1 -2 -3 -3 -1 -2 -2 1 1 3 -1 7
F -3 -2 -3 -4 -2 -4 -3 -3 -2 1 2 -3 0 9
P -2 -3 -2 -2 -5 -2 0 -1 -2 -2 -4 -1 -2 -4 11
S 1 -1 1 0 -1 1 0 0 -1 -2 -3 0 -2 -2 -1 5
T 0 -2 0 -1 -1 -1 -1 -2 -2 -1 -1 0 -1 -1 0 2 6
W -3 -2 -4 -5 -6 -1 -2 -2 -5 -3 -1 -2 -2 1 -4 -5 -4 19
Y -2 -1 -2 -3 -4 -1 -2 -3 2 0 0 -1 1 4 -3 -2 -1 3 9
V 0 -2 -3 -3 -2 -3 -3 -4 -4 4 2 -2 1 0 -3 -1 1 -3 -1 5
B -1 -1 4 6 -2 0 1 -1 0 -3 -3 0 -3 -3 -2 0 0 -4 -3 -3 5
Z -1 0 0 1 -3 4 5 -2 0 -4 -2 1 -2 -4 -1 0 -1 -2 -2 -3 2 5
X 0 -1 -1 -1 -2 -1 -1 -1 -1 -1 -1 -1 0 -1 -2 0 0 -2 -1 -1 -1 -1 -1
A R N D C Q E G H I L K M F P S T W Y V B Z X
- We fill in the BLOSUM40 similarity scores for you in Table 4.
- To turn this
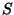 matrix intro the dynamic programming
matrix intro the dynamic programming 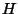 matrix requires
calculation of the contents of all 170 boxes. We've calculated the first 4
here, and encourage you to calculate the contents of at least 4 more. The
practice will come in handy in the next steps. As described above, a matrix square
cannot be filled with its dynamic programming value until the squares above, to
the left, and to the above-left diagonal are computed. The value of a square is
matrix requires
calculation of the contents of all 170 boxes. We've calculated the first 4
here, and encourage you to calculate the contents of at least 4 more. The
practice will come in handy in the next steps. As described above, a matrix square
cannot be filled with its dynamic programming value until the squares above, to
the left, and to the above-left diagonal are computed. The value of a square is
, using the convention that 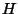 values appear in the top part of a square in
large print, and
values appear in the top part of a square in
large print, and 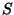 values appear in the bottom part of a square in small
print. Our gap penalty
values appear in the bottom part of a square in small
print. Our gap penalty 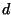 is 8.
is 8.
- Example: In the upper left square in Table 4, square (1,1), the similarity score
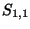 is -1, the number in small type at the bottom of the box. The value to assign as
is -1, the number in small type at the bottom of the box. The value to assign as 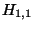 will be the greatest (``max'') of these three values:
will be the greatest (``max'') of these three values:
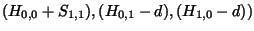 . That is, the greatest of:
. That is, the greatest of:
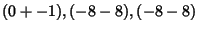 which just means the greatest of: -1, -16, and -16. This is -1, so we write -1 as the value of
which just means the greatest of: -1, -16, and -16. This is -1, so we write -1 as the value of 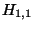 (the larger number in the top part of the box).
The same reasoning in square (2,1) leads us to set
(the larger number in the top part of the box).
The same reasoning in square (2,1) leads us to set 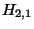 as -9, and so on.
as -9, and so on.
Note: we consider 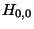 to be the ``predecessor'' of
to be the ``predecessor'' of 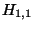 ,
since it helped decided
,
since it helped decided 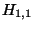 's value. Later, predecessors will qualify to be on the
traceback path.
's value. Later, predecessors will qualify to be on the
traceback path.
- Again, just fill in 4 or 5 boxes in Table 4 until you
get a feel for gap penalties and similarity scores S vs. alignment scores H.
In the next step, we provide the matrix with all values filled in as
Table 5. Check that your 4 or 5 calculations match.
- Now we move to Table 5, with all 170
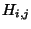 values are shown, to do the ``alignment traceback''. To find the alignment requires one to trace the
path through from the end of the sequence (the lower right box) to the start of the sequence (the upper left box). This job looks complicated, but should only take about 5 -7 minutes.
values are shown, to do the ``alignment traceback''. To find the alignment requires one to trace the
path through from the end of the sequence (the lower right box) to the start of the sequence (the upper left box). This job looks complicated, but should only take about 5 -7 minutes.
- We are tracing a path in Table 5, from the lower right box to the upper left box.
You can only move to a square if it could have been a ``predecessor'' of your
current square - that is, when the matrix was being filled with
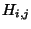 values, the move from the predecessor square to your current
square would have followed the mathematical rules we used to find H
values, the move from the predecessor square to your current
square would have followed the mathematical rules we used to find H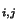 above. Circle each square you move to along your path.
above. Circle each square you move to along your path.
- Example: we start at the lower right square (10,17), where
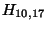 is
-21 and
is
-21 and 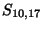 is -2. We need to test for 3 possible directions of
movement: diagonal (up + left), up, and left. The condition for diagonal
movement given above is:
is -2. We need to test for 3 possible directions of
movement: diagonal (up + left), up, and left. The condition for diagonal
movement given above is:
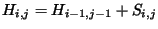 , so for the
diagonal box (9,16) to have contributed to (10,17),
, so for the
diagonal box (9,16) to have contributed to (10,17),
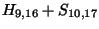 would have to equal the H value of our box, -21. Since (-29 + -2) does not
equal -21, the diagonal box is not a ``predecessor'', so we can't move in that
direction. We try the rule for the box to the left:
would have to equal the H value of our box, -21. Since (-29 + -2) does not
equal -21, the diagonal box is not a ``predecessor'', so we can't move in that
direction. We try the rule for the box to the left:
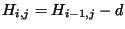 Since -37 - 8 does not equal -21, we also can't move left. Our last chance is
moving up. We test
Since -37 - 8 does not equal -21, we also can't move left. Our last chance is
moving up. We test
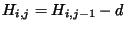 . Since -21 = (-13 - 8) we can
move up! Draw an arrow from the lower right box, (
. Since -21 = (-13 - 8) we can
move up! Draw an arrow from the lower right box, (
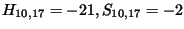 ) to
the box just above it, (
) to
the box just above it, (
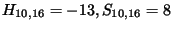 ) .
) .
- Continue moving squares, drawing arrows, and circling each new square you
land on, until you have reached the upper right corner of the matrix If the path
branches, follow both branches.
- Write down the alignment(s) that corresponds to your path(s) by writing
the the letter codes on the margins of each position along your circled path.
Aligned pairs are at the boxes at which the path exits via the upper-left corner.
When there are horizontal or vertical movements movements along your path,
there will be a gap (write as a dash, ``-'') in your sequence.
- Now to check your results against a computer program. We have prepared a
pairwise Needleman-Wunsch alignment program, pair, which you will apply to the same
sequences which you have just manually aligned.
- Change your directory by typing at the Unix prompt:
cd
~/tbss.work/Bioinformatics/pairData
then start the pair alignment executable by typing:
pair targlist
. All alignments will be carried out using the BLOSUM40
matrix, with a gap penalty of 8. The paths to the input files and the
BLOSUM40 matrix used are defined in the file targlist; the BLOSUM40 matrix is the
first 25 lines of the file blosum40. (Other substitution matrices
can be found at the NCBI/Blast website.)
Note: In some installations, the pair executable is
in ~/tbss.work/Bioinformatics/pairData and here you must
type ./pair targlist to run it.
If you cannot access the pair
executable at all, you can see the output from this step in ~/tbss.work/Bioinformatics/pairData/example_output/
- After executing the program you will generate three output files namely
align, scorematrix and stats. View the alignment in GCG format by typing less align. The file scorematrix is the 17x10
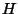 matrix. If there are multiple paths along the traceback matrix, the program pair will choose only one path, by following this precedence rule for existing potential traceback directions, listed in decreasing precedence: diagonal (left and up), up, left.
In the file stats you will find the optimal alignment score and the percent identity of the alignment.
matrix. If there are multiple paths along the traceback matrix, the program pair will choose only one path, by following this precedence rule for existing potential traceback directions, listed in decreasing precedence: diagonal (left and up), up, left.
In the file stats you will find the optimal alignment score and the percent identity of the alignment.
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width=2...
... output of the {\sf pair} program. Do the alignments match?
}
\end{minipage} }](img216.gif)
Finding homologous pairs of ClassII tRNA synthetases
Homologous proteins are proteins derived from a common ancestral gene.
In this exercise with the Needleman-Wunsch algorithm you will study the
sequence identity of several class II tRNA synthetases, which are either from
Eucarya, Eubacteria or Archaea or differ in the kind of aminoacylation
reaction which they catalyze. Table 6 summarizes the reaction
type, the organism and the PDB accession code and chain name of the
employed Class II tRNA synthetase domains.
Table 6:
Domain types, origins, and accession codes
| Specificity |
Organism |
PDB code:chain |
ASTRAL catalytic domain |
| Aspartyl |
Eubacteria |
1EQR:B |
d1eqrb3 |
| Aspartyl |
Archaea |
1B8A:A |
d1b8aa2 |
| Aspartyl |
Eukarya |
1ASZ:A |
d1asza2 |
| Glycl |
Archaea |
1ATI:A |
d1atia2 |
| Histidyl |
Eubacteria |
1ADJ:C |
d1adjc2 |
| Lysl |
Eubacteria |
1BBW:A |
d1bbwa2 |
| Aspartyl |
Eubacteria |
1EFW:A |
d1efwa3 |
|
- We have have prepared a computer program multiple which will align multiple pairs of proteins.
- Change your directory by typing at the Unix prompt:
cd ~/tbss.work/Bioinformatics/multipleData
then start the alignment executable by typing:
multiple targlist
.
Note: In some installations, the multiple executable is
in ~/tbss.work/Bioinformatics/multipleData and here you must
type ./multiple targlist to run it.
If you cannot access the multiple executable at all, you can see the output from this step in ~/tbss.work/Bioinformatics/multipleData/example_output/
- In the align and stats files you will find all
combinatorial possible pairs of the provided sequences. On a piece of paper,
write the names of the the proteins, grouped by ther domain of life, as listed
in Table 6. Compare sequence identities of aligned proteins
from the same domain of a life, and of aligned proteins from different domains
of life, to help answer the questions below.


Next: Sequence and structural alignments
Up: Bioinformatics Tutorial
Previous: SCOP fold classification
zan@uiuc.edu
![]() and
and ![]() . The alignment algorithm is based on
finding the elements of a matrix
. The alignment algorithm is based on
finding the elements of a matrix ![]() where the element
where the element ![]() is the
optimal score for aligning the sequence (
is the
optimal score for aligning the sequence (![]() ,
,![]() ,...,
,...,![]() ) with
(
) with
(![]() ,
,![]() ,.....,
,.....,![]() ). Two similar amino acids (e.g. arginine and lysine)
receive a high score, two dissimilar amino acids (e.g. arginine and glycine)
receive a low score. The higher the score of a path through the matrix, the better
the alignment. The matrix
). Two similar amino acids (e.g. arginine and lysine)
receive a high score, two dissimilar amino acids (e.g. arginine and glycine)
receive a low score. The higher the score of a path through the matrix, the better
the alignment. The matrix ![]() is found by progressively finding the matrix
elements, starting at
is found by progressively finding the matrix
elements, starting at ![]() and proceeding in the directions of increasing
and proceeding in the directions of increasing
![]() and
and ![]() . Each element is set according to:
. Each element is set according to:
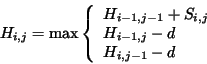
![]() is the similarity score of comparing amino acid
is the similarity score of comparing amino acid ![]() to amino
acid
to amino
acid ![]() (obtained here from the BLOSUM40 similarity table) and
(obtained here from the BLOSUM40 similarity table) and ![]() is the
penalty for a single gap. The matrix is initialized with
is the
penalty for a single gap. The matrix is initialized with ![]() . When
obtaining the local Smith-Waterman alignment,
. When
obtaining the local Smith-Waterman alignment, ![]() is modified:
is modified:
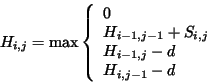
![]() can be replaced by
can be replaced by
![]() , where
, where ![]() is the penalty for a single gap
and
is the penalty for a single gap
and ![]() is the number of consecutive gaps.
is the number of consecutive gaps.
![]() along
the optimal path is found, which corresponds to the the optimal sequence
alignment for the score. In the next set of exercises you will manually
implement the Needleman-Wunsch alignment for a pair of short sequences, then
perform global sequence alignments with a computer program developed by Anurag
Sethi, which is based on the Needleman-Wunsch algorithm with an affine gap
penalty,
along
the optimal path is found, which corresponds to the the optimal sequence
alignment for the score. In the next set of exercises you will manually
implement the Needleman-Wunsch alignment for a pair of short sequences, then
perform global sequence alignments with a computer program developed by Anurag
Sethi, which is based on the Needleman-Wunsch algorithm with an affine gap
penalty, ![]() , where
, where ![]() is the extension gap penalty. The output
file will be in the GCG format, one of the two standard formats in
bioinformatics for storing sequence information (the other standard format is
FASTA).
is the extension gap penalty. The output
file will be in the GCG format, one of the two standard formats in
bioinformatics for storing sequence information (the other standard format is
FASTA).
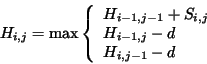
![]() values appear in the top part of a square in
large print, and
values appear in the top part of a square in
large print, and ![]() values appear in the bottom part of a square in small
print. Our gap penalty
values appear in the bottom part of a square in small
print. Our gap penalty ![]() is 8.
is 8.
![]() to be the ``predecessor'' of
to be the ``predecessor'' of ![]() ,
since it helped decided
,
since it helped decided ![]() 's value. Later, predecessors will qualify to be on the
traceback path.
's value. Later, predecessors will qualify to be on the
traceback path.
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width=2...
... output of the {\sf pair} program. Do the alignments match?
}
\end{minipage} }](img216.gif)
![\framebox[\textwidth]{
\begin{minipage}{.2\textwidth}
\includegraphics[width=2...
...utionarily divergent pair according to the sequence identity?}
\end{minipage} }](img217.gif)