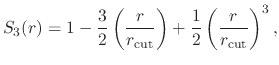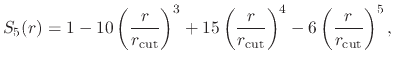



Next: Temperature Control and Equilibration
Up: Standard Minimization and Dynamics
Previous: Energy Minimization
Contents
Index
Subsections
Dynamics
- zeroMomentum
 remove center of mass drift due to PME
remove center of mass drift due to PME 
Acceptable Values: yes or no
Default Value: no
Description:
If enabled, the net momentum of the simulation and any resultant drift
is removed before every full electrostatics step.
This correction should conserve energy and have minimal impact on
parallel scaling.
This feature should only be used for simulations that would
conserve momentum except for the slight errors in PME.
(Features such as fixed atoms, harmonic restraints, steering forces,
and Langevin dynamics do not conserve momentum; use in combination
with these features should be considered experimental.)
Since the momentum correction is delayed, enabling outputMomenta
will show a slight nonzero linear momentum but there should be no
center of mass drift.
Multiple timestep parameters
To further reduce the cost of computing full electrostatics,
NAMD uses a multiple timestepping integration scheme. In this scheme,
the total force acting on each atom is broken into two pieces, a quickly varying local
component and a slower long range component.
The local force component is defined in terms of a splitting function. The local force component consists of all bonded and van der Waals interactions
as well as that portion of electrostatic interactions for pairs that are separated by less than the local interaction distance determined by the splitting function.
The long range component consists only of
electrostatic interactions outside of the local interaction distance.
Since the long range forces are slowly varying, they are not evaluated
every timestep. Instead, they are evaluated every 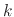 timesteps,
specified by the NAMD parameter fullElectFrequency.
An impulse of
timesteps,
specified by the NAMD parameter fullElectFrequency.
An impulse of 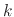 times the long range force is applied to the system
every
times the long range force is applied to the system
every 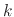 timesteps (i.e., the r-RESPA integrator is used).
For appropriate values of
timesteps (i.e., the r-RESPA integrator is used).
For appropriate values of 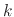 ,
it is believed that the error introduced by this infrequent evaluation
is modest compared to the error already incurred by the use of the numerical
(Verlet) integrator.
Improved methods for incorporating these long range forces
are currently being investigated,
with the intention of improving accuracy as well as
reducing the frequency of long range force evaluations.
,
it is believed that the error introduced by this infrequent evaluation
is modest compared to the error already incurred by the use of the numerical
(Verlet) integrator.
Improved methods for incorporating these long range forces
are currently being investigated,
with the intention of improving accuracy as well as
reducing the frequency of long range force evaluations.
In the scheme described above, the van der Waals forces are still
truncated at the local interaction distance.
Thus, the van der Waals cutoff distance
forms a lower limit to the local interaction distance. While this is
believed to be sufficient, there are investigations underway to remove
this limitation and provide full van der Waals calculations in
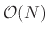 time as well.
time as well.
One of the areas of current research being studied using NAMD is the
exploration of better methods for performing multiple timestep integration.
Currently the only available method is the impulse-based Verlet-I or r-RESPA
method which is stable for timesteps up to 4 fs for long-range electrostatic
forces, 2 fs for short-range nonbonded forces, and 1 fs for bonded forces
Setting rigid all (i.e., using SHAKE) increases these timesteps to
6 fs, 2 fs, and 2 fs respectively but eliminates bond motion for hydrogen.
The mollified impulse method (MOLLY) reduces the resonance which limits
the timesteps and thus increases these timesteps to 6 fs, 2 fs, and 1 fs
while retaining all bond motion.
- fullElectFrequency
 number of timesteps between full electrostatic evaluations
number of timesteps between full electrostatic evaluations 
Acceptable Values: positive integer factor of stepspercycle
Default Value: nonbondedFreq
Description: This parameter specifies the number of timesteps between each full electrostatics evaluation.
It is recommended that fullElectFrequency be chosen so that
the product of fullElectFrequency and timestep does
not exceed 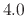 unless rigidBonds all or molly on is specified,
in which case the upper limit is perhaps doubled.
unless rigidBonds all or molly on is specified,
in which case the upper limit is perhaps doubled.
- nonbondedFreq
 timesteps between nonbonded evaluation
timesteps between nonbonded evaluation 
Acceptable Values: positive integer factor of fullElectFrequency
Default Value: 1
Description: This parameter specifies how often short-range nonbonded interactions should be calculated. Setting nonbondedFreq between 1 and fullElectFrequency allows triple timestepping where, for example, one could evaluate bonded forces every 1 fs, short-range nonbonded forces every 2 fs, and long-range electrostatics every 4 fs.
- MTSAlgorithm
 MTS algorithm to be used
MTS algorithm to be used 
Acceptable Values: impulse/verletI or constant/naive
Default Value: impulse
Description: Specifies the multiple timestep algorithm used to integrate the
long and short range forces. impulse/verletI is the same as r-RESPA.
constant/naive is the stale force extrapolation method.
- longSplitting
 how should long and short range forces be split?
how should long and short range forces be split? 
Acceptable Values: c1, c2
Default Value: c1
Description: Specifies the method used to split electrostatic forces between long
and short range potentials.
The c1 option uses a cubic polynomial splitting function,
to affect 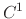 continuity in the splitting of the electrostatic potential
[68].
The c2 option uses a quintic polynomial splitting function,
continuity in the splitting of the electrostatic potential
[68].
The c2 option uses a quintic polynomial splitting function,
to affect 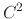 continuity in the splitting of the electrostatic potential.
The
continuity in the splitting of the electrostatic potential.
The 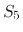 splitting function,
contributed by Bruce Berne, Ruhong Zhou, and Joe Morrone,
produces demonstrably better long time stability than
splitting function,
contributed by Bruce Berne, Ruhong Zhou, and Joe Morrone,
produces demonstrably better long time stability than 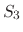 without requiring any additional
computational cost during simulation,
since the nonbonded forces are calculated via a lookup table.
Note that earlier options
xplor and sharp are no longer supported.
without requiring any additional
computational cost during simulation,
since the nonbonded forces are calculated via a lookup table.
Note that earlier options
xplor and sharp are no longer supported.
- molly
 use mollified impulse method (MOLLY)?
use mollified impulse method (MOLLY)? 
Acceptable Values: on or off
Default Value: off
Description:
This method eliminates the components of the long range electrostatic
forces which contribute to resonance along bonds to hydrogen atoms,
allowing a fullElectFrequency of 6 (vs. 4) with a 1 fs timestep
without using rigidBonds all. You may use rigidBonds water but
using rigidBonds all with MOLLY makes no sense since the degrees of
freedom which MOLLY protects from resonance are already frozen.
- mollyTolerance
 allowable error for MOLLY
allowable error for MOLLY 
Acceptable Values: positive decimal
Default Value: 0.00001
Description:
Convergence criterion for MOLLY algorithm.
- mollyIterations
 maximum MOLLY iterations
maximum MOLLY iterations 
Acceptable Values: positive integer
Default Value: 100
Description:
Maximum number of iterations for MOLLY algorithm.




Next: Temperature Control and Equilibration
Up: Standard Minimization and Dynamics
Previous: Energy Minimization
Contents
Index
http://www.ks.uiuc.edu/Research/namd/