



Next: 3-Phase Calculation
Up: Generalized Born Implicit Solvent
Previous: Generalized Born Implicit Solvent
Contents
Index
Subsections
Water has many biologically necessary properties, one of which is as a dielectric.
As a dielectric, water screens (lessens) electrostatic interactions between charged particles.
Water can therefore be crudely modeled as a dielectric continuum.
In this manner, the electrostatic forces of a biological system can be expressed as a system of differential equations which can be solved for the electric field caused by a collection of charges.
The Poisson Boltzmann equation (PBE),
is a nonlinear equation which solves for the electrostatic field,
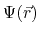 , based on
the position dependent dielectric,
, based on
the position dependent dielectric,
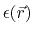 ,
the position-dependent accessibility of position
,
the position-dependent accessibility of position 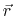 to the ions in solution,
to the ions in solution,
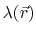 ,
the solute charge distribution,
,
the solute charge distribution,
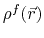 ,
and the bulk charge density,
,
and the bulk charge density,
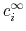 , of ion
, of ion 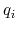 .
While this equation does exactly solve for the electrostic field of a charge distribution in a dielectric, it is very expensive to solve, and therefore not suitable for molecular dynamics.
.
While this equation does exactly solve for the electrostic field of a charge distribution in a dielectric, it is very expensive to solve, and therefore not suitable for molecular dynamics.
The Generalized Born (GB) equation is an approximation of the PBE.
It models atoms as charged spheres whose internal dielectric is lower than that of the environment.
The screening which each atom, 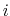 , experiences is determined by the local environment;
the more atom
, experiences is determined by the local environment;
the more atom 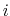 is surrounded by other atoms, the less it's electrostatics will be screened since it is more surrounded by low dielectric; this property is called one atom descreening another.
Different GB models calculate atomic descreening differently.
Descreening is used to calculate the Born radius,
is surrounded by other atoms, the less it's electrostatics will be screened since it is more surrounded by low dielectric; this property is called one atom descreening another.
Different GB models calculate atomic descreening differently.
Descreening is used to calculate the Born radius, 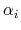 , of each atom.
The Born radius of an atom measures the degree of descreening.
A large Born radius represents small screening (strong electric field) as if the atom were in vacuum.
A small Born radius represents large screening (weak electric field) as if the atom were in bulk water.
The next section describes how the Born radius is calculated and how it is used to calculate electrostatics.
, of each atom.
The Born radius of an atom measures the degree of descreening.
A large Born radius represents small screening (strong electric field) as if the atom were in vacuum.
A small Born radius represents large screening (weak electric field) as if the atom were in bulk water.
The next section describes how the Born radius is calculated and how it is used to calculate electrostatics.
In a GB simulation, the total electrostatic force on an atom, 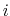 , is the net Coulomb force on atom
, is the net Coulomb force on atom 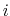 (from nearby atoms) minus the GB force on atom
(from nearby atoms) minus the GB force on atom 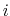 (also caused by nearby atoms):
(also caused by nearby atoms):
Forces are contributed by other nearby atoms within a cutoff.
The GB force on atom 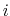 is the derivative of the total GB energy with respect to relative atom distances
is the derivative of the total GB energy with respect to relative atom distances 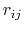 ,
,
where the partial derivatives are included since the Born radius, 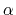 , is a function of all relative atom distances.
The total GB energy of the system is
, is a function of all relative atom distances.
The total GB energy of the system is
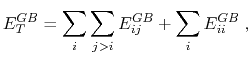 |
(11) |
where
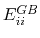 is the Born radius dependent self energy of atom
is the Born radius dependent self energy of atom 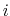 , and the GB energy between atoms
, and the GB energy between atoms 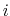 and
and 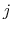 is given by
is given by
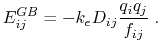 |
(12) |
The dielectric term [88] is
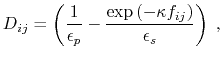 |
(13) |
and the GB function [90] is
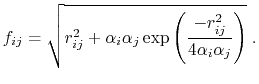 |
(14) |
As the Born radii of atoms 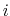 and
and 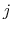 decrease (increasing screening), the effective distance between the atoms (
decrease (increasing screening), the effective distance between the atoms (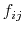 ) increases.
The implicit solvent implemented in NAMD is the model of Onufriev, Bashford and Case [71,72] which calculates the Born radius as
) increases.
The implicit solvent implemented in NAMD is the model of Onufriev, Bashford and Case [71,72] which calculates the Born radius as
![$\displaystyle \alpha_k = \left[ \frac{1}{\rho_{k0}} - \frac{1}{\rho_k}\textrm{tanh}\left(\delta\psi_k - \beta\psi_k^2 + \gamma\psi_k^3\right)\right]^{-1}$](img124.png) |
(15) |
where
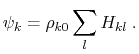 |
(16) |
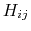 is the piecewise descreening function [72,41,81]; the seven piecewise regimes are
is the piecewise descreening function [72,41,81]; the seven piecewise regimes are
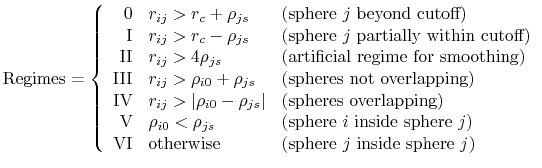 |
(17) |
and the values of 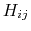 are
are
![$\displaystyle H_{ij} = \left\{ \begin{array}{r l} \textrm{0} & 0 \\ \textrm{I} ...
...ho_{js}-r_{ij}}{r_{ij}+\rho_{js}} \right]\\ \textrm{VI} & 0 \end{array} \right.$](img128.png) |
(18) |
Below are defined the derivatives of the above functions which are required for force calculations.
![$\displaystyle \frac{\partial E_{ij}}{\partial r_{ij}} = - k_e \left[ \frac{q_i ...
...\frac{q_i q_j D_{ij}}{f_{ij}^2} \frac{\partial f_{ij}}{\partial r_{ij}} \right]$](img129.png) |
(19) |
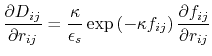 |
(20) |
![$\displaystyle \frac{\partial f_{ij}}{\partial r_{ij}} = \frac{r_{ij}}{f_{ij}} \...
... - \frac{1}{4} \exp{\left(\frac{-r_{ij}^2}{4 \alpha_i \alpha_j}\right)} \right]$](img131.png) |
(21) |
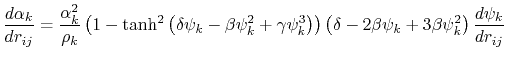 |
(22) |
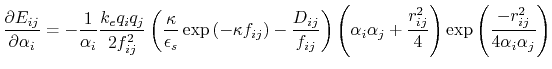 |
(27) |
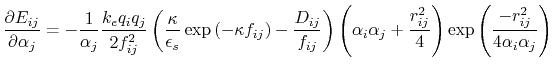 |
(28) |
![$\displaystyle \frac{\partial H_{ij}}{\partial r_{ij}} = \left\{ \begin{array}{r...
...o_{js}-r_{ij}}{r_{ij}+\rho_{js}} \right] \\ \textrm{VI} & 0 \end{array} \right.$](img143.png) |
(29) |
Other variables referenced in the above GB equations are
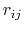 - distance between atoms i and j; calculated from atom coordinates.
- distance between atoms i and j; calculated from atom coordinates.
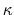 - debye screening length; calculated from ion concentration,
- debye screening length; calculated from ion concentration,
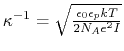 ;
;
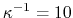 Å for 0.1 M monovalent salt.
Å for 0.1 M monovalent salt.
-
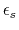 - dielectric constant of solvent.
- dielectric constant of solvent.
-
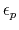 - dielectric constant of protein.
- dielectric constant of protein.
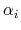 - Born radius of atom
- Born radius of atom 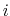 .
.
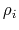 - intrinsic radius of atom
- intrinsic radius of atom 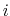 taken from Bondi [10].
taken from Bondi [10].
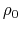 - intrinsic radius offset;
- intrinsic radius offset;
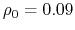 Å by default [72].
Å by default [72].
-
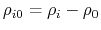
-
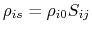
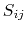 - atom radius scaling factor [41,88].
- atom radius scaling factor [41,88].
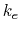 - Coulomb's constant,
- Coulomb's constant,
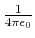 , 332.063711 kcal Å / e
, 332.063711 kcal Å / e .
.
-
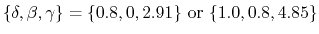 [72]
[72]




Next: 3-Phase Calculation
Up: Generalized Born Implicit Solvent
Previous: Generalized Born Implicit Solvent
Contents
Index
http://www.ks.uiuc.edu/Research/namd/
![$\displaystyle \vec{\nabla} \cdot \left[ \epsilon (\vec{r}) \vec{\nabla} \Psi(\v...
..._i \lambda(\vec{r}) \cdot \exp \left[ \frac{-q_i \Psi(\vec{r})}{k_B T} \right]
$](img102.png)
![$\displaystyle \vec{\nabla} \cdot \left[ \epsilon (\vec{r}) \vec{\nabla} \Psi(\v...
..._i \lambda(\vec{r}) \cdot \exp \left[ \frac{-q_i \Psi(\vec{r})}{k_B T} \right]
$](img102.png)
![$\displaystyle -\sum_j \left[ \frac{d E_T^{GB}}{d r_{ij}} \right] \hat{r}_{ji}$](img113.png)
![$\displaystyle -\sum_j \left[ \sum_k \frac{\partial E_T^{GB}}{\partial \alpha_k}...
...}{d r_{ij}} + \frac{\partial E_{ij}^{GB}}{\partial r_{ij}} \right] \hat{r}_{ji}$](img114.png)
![$\displaystyle -\sum_j \left[ \frac{\partial E_T^{GB}}{\partial \alpha_i}\frac{d...
...r_{ij}}+ \frac{\partial E_{ij}^{GB}}{\partial r_{ij}} \right] \hat{r}_{ji} \; .$](img115.png)
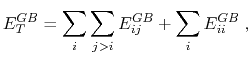
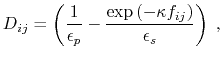
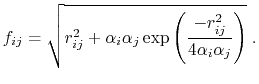
![$\displaystyle \alpha_k = \left[ \frac{1}{\rho_{k0}} - \frac{1}{\rho_k}\textrm{tanh}\left(\delta\psi_k - \beta\psi_k^2 + \gamma\psi_k^3\right)\right]^{-1}$](img124.png)
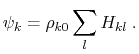
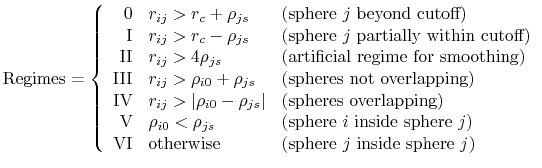
![$\displaystyle H_{ij} = \left\{ \begin{array}{r l} \textrm{0} & 0 \\ \textrm{I} ...
...ho_{js}-r_{ij}}{r_{ij}+\rho_{js}} \right]\\ \textrm{VI} & 0 \end{array} \right.$](img128.png)
![$\displaystyle \frac{\partial E_{ij}}{\partial r_{ij}} = - k_e \left[ \frac{q_i ...
...\frac{q_i q_j D_{ij}}{f_{ij}^2} \frac{\partial f_{ij}}{\partial r_{ij}} \right]$](img129.png)
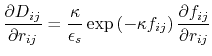
![$\displaystyle \frac{\partial f_{ij}}{\partial r_{ij}} = \frac{r_{ij}}{f_{ij}} \...
... - \frac{1}{4} \exp{\left(\frac{-r_{ij}^2}{4 \alpha_i \alpha_j}\right)} \right]$](img131.png)
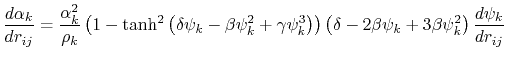
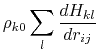
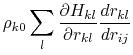
![$\displaystyle \rho_{k0} \left[ \frac{\partial H_{kj}}{\partial r_{kj}}\delta_{ki} + \frac{\partial H_{ki}}{\partial r_{ki}}\delta_{kj} \right]$](img136.png)
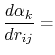
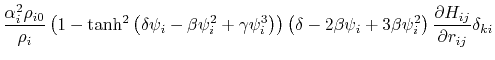
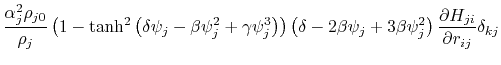
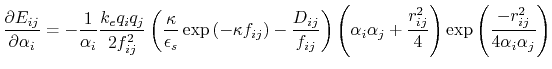
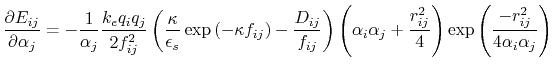
![$\displaystyle \frac{\partial H_{ij}}{\partial r_{ij}} = \left\{ \begin{array}{r...
...o_{js}-r_{ij}}{r_{ij}+\rho_{js}} \right] \\ \textrm{VI} & 0 \end{array} \right.$](img143.png)
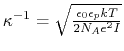 ;
;