



Next: Introduction
Up: NAMD 2.13 User's Guide
Previous: Contents
Contents
Index
- Graph of van der Waals potential with and without switching
- Graph of electrostatic potential with and without shifting function
- Graph of electrostatic split between short and long range forces
- Graph showing a slice of a ramp potential, showing the effect of
mgridforcevoff
- Graphical representation of a Colvars configuration.
- Dual topology description for an alchemical simulation.
Case example of the mutation of alanine into serine.
The lighter color denotes the non-interacting, alternate
state.
- Convergence of an FEP calculation. If the ensembles representative
of states
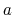 and
and 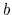 are too disparate, equation (67) will
not converge (a).
If, in sharp contrast, the configurations of
state
are too disparate, equation (67) will
not converge (a).
If, in sharp contrast, the configurations of
state 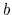 form a subset of the ensemble of configurations
characteristic of state
form a subset of the ensemble of configurations
characteristic of state 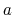 , the simulation is expected
to converge (b).
The difficulties reflected in case (a) may be
alleviated by the introduction of mutually overlapping intermediate
states that connect
, the simulation is expected
to converge (b).
The difficulties reflected in case (a) may be
alleviated by the introduction of mutually overlapping intermediate
states that connect 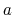 to
to 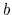 (c). It should be
mentioned that in practice, the kinetic contribution,
(c). It should be
mentioned that in practice, the kinetic contribution,
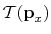 ,
is assumed to be identical for state
,
is assumed to be identical for state 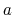 and state
and state 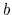 .
.
- Relationship of user-defined
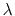 to coupling of electrostatic or vdW interactions to a simulation, given specific values of alchElecLambdaStart or alchVdwLambdaEnd.
to coupling of electrostatic or vdW interactions to a simulation, given specific values of alchElecLambdaStart or alchVdwLambdaEnd.
- Sample TI data (
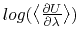 against
against 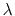 ). The blue shaded
area shows the integral with fine sampling close to the end point. The red area
shows the difference when
). The blue shaded
area shows the integral with fine sampling close to the end point. The red area
shows the difference when 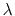 values are more sparse. In this example,
insufficient sampling before
values are more sparse. In this example,
insufficient sampling before 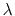
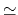 0.1 can result in a large overestimation
of the integral. Beyond
0.1 can result in a large overestimation
of the integral. Beyond 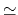 0.2, sparser sampling is justified as dE/d
0.2, sparser sampling is justified as dE/d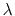 is not
changing quickly.
is not
changing quickly.
- Schematics of the aMD method. When the original potential (thick line) falls below a threshold energy
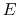 (dashed line),
a boost potential is added. The modified energy profiles (thin lines) have smaller barriers separating adjacent
energy basins.
(dashed line),
a boost potential is added. The modified energy profiles (thin lines) have smaller barriers separating adjacent
energy basins.
- Schematic illustration of GaMD. When the threshold energy
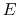 is set to the maximum potential (
is set to the maximum potential (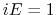 mode), the system's potential energy surface is smoothened by adding a harmonic boost potential that follows a Gaussian distribution. The coefficient
mode), the system's potential energy surface is smoothened by adding a harmonic boost potential that follows a Gaussian distribution. The coefficient 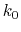 , which falls in the range of
, which falls in the range of 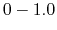 , determines the magnitude of the applied boost potential.
, determines the magnitude of the applied boost potential.
- The core difference between conventional and constant-pH MD can be
illustrated by a simple enzyme
 with four protonation states
describing the occupancy of two titratable residues,
with four protonation states
describing the occupancy of two titratable residues, 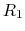 and
and 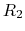 .
A conventional MD simulation handles the states separately (left
panel).
The relative importance of the states must be known beforehand or computed
by other means.
Conversely, a constant-pH MD simulation handles the states
collectively and actively simulates interconversion (right panel).
Determining the relative importance of the states is a direct result of the
simulation.
.
A conventional MD simulation handles the states separately (left
panel).
The relative importance of the states must be known beforehand or computed
by other means.
Conversely, a constant-pH MD simulation handles the states
collectively and actively simulates interconversion (right panel).
Determining the relative importance of the states is a direct result of the
simulation.
- The basic constant-pH MD scheme in NAMD is to alternate equilibrium
sampling in a fixed protonation state followed by a nonequilibrium MD
Monte Carlo move to sample other protonation states.
The latter move can be accepted or rejected.
If accepted, the simulation continues in the new protonation state.
If the move is rejected, sampling continues as if the move were never
attempted at all.
- Hybrid QM/MM NAMD
- Diagram of classical point charge options.
- Treatment of QM/MM bonds
- Charge Groups and QM/MM Bonds
- Diagram of Multiple Grid Regions
- Example of cutoff and pairlist distance uses
http://www.ks.uiuc.edu/Research/namd/