



Next: Water Models
Up: Force Field Parameters
Previous: Potential energy functions
Contents
Index
Subsections
Non-bonded interactions
NAMD has a number of options that control the way that non-bonded
interactions are calculated. These options are interrelated and
can be quite confusing, so this section attempts to explain the
behavior of the non-bonded interactions and how to use these
parameters.
The simplest non-bonded
interaction is the van der Waals interaction. In
NAMD, van der Waals interactions are always truncated at the
cutoff distance, specified by cutoff.
The main option that effects van der Waals interactions
is the switching parameter. With this option set to on,
a smooth switching function will be used to truncate the
van der Waals potential energy smoothly at the cutoff distance.
A graph of the van der Waals
potential with this switching function is shown in Figure
1. If switching is set to off, the
van der Waals energy is just abruptly truncated at the cutoff
distance, so that energy may not be conserved.
Figure 1:
Graph of van der Waals potential with and without the
application of the switching function. With the switching function
active, the potential is smoothly reduced to 0 at the cutoff distance.
Without the switching function, there is a discontinuity where the
potential is truncated.
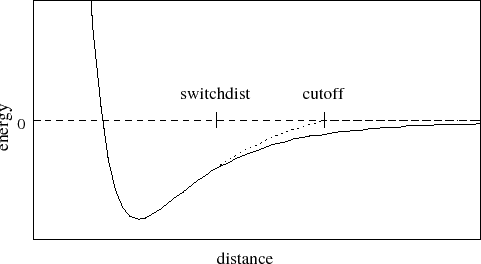 |
The switching function used is based on the X-PLOR switching
function. The parameter switchdist specifies the distance
at which the switching function should start taking effect to
bring the van der Waals potential to 0 smoothly at the cutoff distance.
Thus, the value of switchdist must always be less than that
of cutoff.
The handling of electrostatics is slightly
more complicated due to the incorporation of multiple timestepping for full
electrostatic interactions. There are two cases to consider, one where
full electrostatics is employed and the other where electrostatics
are truncated at a given distance.
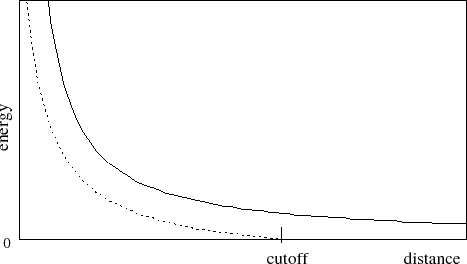
First let us consider the latter case, where electrostatics are truncated at
the cutoff distance. Using this scheme, all electrostatic interactions
beyond a specified distance are ignored, or assumed to be zero. If
switching is set to on, rather than having a discontinuity
in the potential
at the cutoff distance, a shifting function is applied to the electrostatic
potential as shown in Figure 2. As this figure shows, the
shifting function shifts the entire potential curve so that the curve
intersects the x-axis at the cutoff distance. This shifting function
is based on the
shifting function used by X-PLOR.
Figure 2:
Graph showing an electrostatic potential with and without the
application of the shifting function.
 |
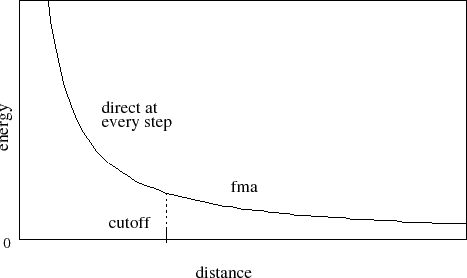
Next, consider the case where full electrostatics are calculated. In this
case, the electrostatic interactions are not truncated at any distance. In
this scheme, the cutoff parameter has a slightly different meaning
for the electrostatic interactions -- it represents
the local interaction distance, or distance within which electrostatic
pairs will be directly calculated every timestep. Outside of this distance,
interactions will be calculated only periodically. These forces
will be applied using a multiple timestep integration scheme as described in
Section 7.3.4.
Figure 3:
Graph showing an electrostatic potential
when full electrostatics are used within NAMD,
with one curve portion calculated directly
and the other calculated using PME.
 |
- cutoff
 local interaction distance common to both electrostatic
and van der Waals calculations (Å)
local interaction distance common to both electrostatic
and van der Waals calculations (Å) 
Acceptable Values: positive decimal
Description: See Section 5.2 for more information.
- switching
 use switching function?
use switching function? 
Acceptable Values: on or off
Default Value: on
Description: If switching is
specified to be off, then a truncated cutoff is performed.
If switching is turned on, then smoothing functions
are applied to both the electrostatics and van der Waals forces.
For a complete description of the non-bonded force parameters see
Section 5.2. If switching is set to
on, then switchdist must also be defined.
- vdwForceSwitching
 use force switching for VDW?
use force switching for VDW? 
Acceptable Values: on or off
Default Value: off
Description: If both switching and vdwForceSwitching are set to on,
then CHARMM force switching is used for van der Waals forces.
- switchdist
 distance at which to activate switching/splitting function
for electrostatic and van der Waals calculations (Å)
distance at which to activate switching/splitting function
for electrostatic and van der Waals calculations (Å) 
Acceptable Values: positive decimal 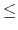 cutoff
cutoff
Description: Distance at which the switching function
should begin to take effect.
This parameter only has meaning if switching is
set to on.
The value of switchdist must be less than
or equal to the value of cutoff, since the switching function
is only applied on the range from switchdist to cutoff.
For a complete description of the non-bonded force parameters see
Section 5.2.
- exclude
 non-bonded exclusion policy to use
non-bonded exclusion policy to use 
Acceptable Values: none, 1-2, 1-3, 1-4, or scaled1-4
Description: This parameter specifies which pairs of bonded atoms should
be excluded from non-bonded
interactions. With the value of none, no bonded pairs of atoms
will be excluded. With the value of 1-2, all atom pairs that
are directly connected via a linear bond will be excluded. With the
value of 1-3, all 1-2 pairs will be excluded along with
all pairs of atoms that are bonded to a common
third atom (i.e., if atom A is bonded to atom B and atom B is bonded
to atom C, then the atom pair A-C would be excluded).
With the value of 1-4, all 1-3 pairs will be excluded along
with all pairs connected by a set of two bonds (i.e., if atom A is bonded
to atom B, and atom B is bonded to atom C, and atom C is bonded to
atom D, then the atom pair A-D would be excluded). With the value
of scaled1-4, all 1-3 pairs are excluded and all pairs
that match the 1-4 criteria are modified. The electrostatic
interactions for such pairs are modified by the constant factor
defined by 1-4scaling.
The van der Waals interactions are modified
by using the special 1-4 parameters defined in the parameter files.
The value of scaled1-4 is necessary to enable the modified
1-4 VDW parameters present in the CHARMM parameter files.
- 1-4scaling
 scaling factor for 1-4 electrostatic interactions
scaling factor for 1-4 electrostatic interactions 
Acceptable Values: 0 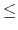 decimal
decimal 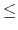 1
1
Default Value: 1.0
Description: Scaling factor for 1-4 electrostatic interactions.
This factor is only used when the
exclude parameter is set to scaled1-4. In this case, this
factor is used to modify the electrostatic interactions between 1-4 atom
pairs. If the exclude parameter is set to anything but
scaled1-4, this parameter has no effect regardless of its value.
- dielectric
 dielectric constant for system
dielectric constant for system 
Acceptable Values: decimal 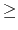 1.0
1.0
Default Value: 1.0
Description: Dielectric constant for the system. A value of 1.0 implies no modification
of the electrostatic interactions. Any larger value will lessen the
electrostatic forces acting in the system.
- nonbondedScaling
 scaling factor for nonbonded forces
scaling factor for nonbonded forces 
Acceptable Values: decimal 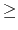 0.0
0.0
Default Value: 1.0
Description: Scaling factor for electrostatic and van der Waals forces.
A value of 1.0 implies no modification of the interactions.
Any smaller value will lessen the
nonbonded forces acting in the system.
- vdwGeometricSigma
 use geometric mean to combine L-J sigmas
use geometric mean to combine L-J sigmas 
Acceptable Values: yes or no
Default Value: no
Description: Use geometric mean, as required by OPLS, rather than
traditional arithmetic mean when combining Lennard-Jones sigma parameters
for different atom types.
- limitdist
 maximum distance between pairs for limiting interaction strength(Å)
maximum distance between pairs for limiting interaction strength(Å) 
Acceptable Values: non-negative decimal
Default Value: 0.
Description:
The electrostatic and van der Waals potential functions diverge
as the distance between two atoms approaches zero.
The potential for atoms closer than limitdist is instead
treated as 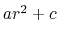 with parameters chosen to match the
force and potential at limitdist.
This option should primarily be useful for alchemical free energy
perturbation calculations, since it makes the process of creating
and destroying atoms far less drastic energetically.
The larger the value of limitdist the more the maximum force
between atoms will be reduced.
In order to not alter the other interactions in the simulation,
limitdist should be less than the closest approach
of any non-bonded pair of atoms; 1.3Å appears to satisfy this
for typical simulations but the user is encouraged to experiment.
There should be no performance impact from enabling this feature.
with parameters chosen to match the
force and potential at limitdist.
This option should primarily be useful for alchemical free energy
perturbation calculations, since it makes the process of creating
and destroying atoms far less drastic energetically.
The larger the value of limitdist the more the maximum force
between atoms will be reduced.
In order to not alter the other interactions in the simulation,
limitdist should be less than the closest approach
of any non-bonded pair of atoms; 1.3Å appears to satisfy this
for typical simulations but the user is encouraged to experiment.
There should be no performance impact from enabling this feature.
- LJcorrection
 Apply long-range corrections to the system energy and virial to
account for neglected vdW forces?
Apply long-range corrections to the system energy and virial to
account for neglected vdW forces? 
Acceptable Values: yes or no
Default Value: no
Description: Apply an analytical correction to the reported vdW energy and virial
that is equal to the amount lost due to switching and cutoff of the LJ
potential. The correction will use the average of vdW parameters for
all particles in the system and assume a constant, homogeneous
distribution of particles beyond the switching distance. See
[89] for details (the equations used in the NAMD
implementation are slightly different due to the use of a different
switching function). Periodic boundary conditions are required to make
use of tail corrections.
PME stands for Particle Mesh Ewald and is an efficient
full electrostatics method for use with periodic boundary conditions.
None of the parameters should affect energy conservation, although they may affect the accuracy of the results and momentum conservation.
- PME
 Use particle mesh Ewald for electrostatics?
Use particle mesh Ewald for electrostatics? 
Acceptable Values: yes or no
Default Value: no
Description: Turns on particle mesh Ewald.
- PMETolerance
 PME direct space tolerance
PME direct space tolerance 
Acceptable Values: positive decimal
Default Value: 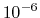
Description: Affects the value of the Ewald coefficient and the overall accuracy of the results.
- PMEInterpOrder
 PME interpolation order
PME interpolation order 
Acceptable Values: positive integer
Default Value: 4 (cubic)
Description: Charges are interpolated onto the grid and forces are interpolated off using this many points, equal to the order of the interpolation function plus one.
- PMEGridSpacing
 maximum space between grid points
maximum space between grid points 
Acceptable Values: positive real
Description: The grid spacing partially determines the accuracy and efficiency of PME.
If any of the grid sizes below are not set, then PMEGridSpacing must be set
(recommended value is 1.0 Å) and will be used to calculate them.
If a grid size is set, then the grid spacing must be
at least PMEGridSpacing (if set, or a very large default of 1.5).
- PMEGridSizeX
 number of grid points in x dimension
number of grid points in x dimension 
Acceptable Values: positive integer
Description: The grid size partially determines the accuracy and efficiency of PME.
For speed, PMEGridSizeX should have only small integer factors (2, 3 and 5).
- PMEGridSizeY
 number of grid points in y dimension
number of grid points in y dimension 
Acceptable Values: positive integer
Description: The grid size partially determines the accuracy and efficiency of PME.
For speed, PMEGridSizeY should have only small integer factors (2, 3 and 5).
- PMEGridSizeZ
 number of grid points in z dimension
number of grid points in z dimension 
Acceptable Values: positive integer
Description: The grid size partially determines the accuracy and efficiency of PME.
For speed, PMEGridSizeZ should have only small integer factors (2, 3 and 5).
- PMEProcessors
 processors for FFT and reciprocal sum
processors for FFT and reciprocal sum 
Acceptable Values: positive integer
Default Value: larger of x and y grid sizes up to all available processors
Description: For best performance on some systems and machines, it may be necessary to
restrict the amount of parallelism used. Experiment with this parameter if
your parallel performance is poor when PME is used.
- FFTWEstimate
 Use estimates to optimize FFT?
Use estimates to optimize FFT? 
Acceptable Values: yes or no
Default Value: no
Description: Do not optimize FFT based on measurements, but on FFTW rules of thumb.
This reduces startup time, but may affect performance.
- FFTWUseWisdom
 Use FFTW wisdom archive file?
Use FFTW wisdom archive file? 
Acceptable Values: yes or no
Default Value: yes
Description: Try to reduce startup time when possible by reading FFTW ``wisdom'' from a file, and saving wisdom generated by performance measurements to the same file for future use.
This will reduce startup time when running the same size PME grid on the same number of processors as a previous run using the same file.
- FFTWWisdomFile
 name of file for FFTW wisdom archive
name of file for FFTW wisdom archive 
Acceptable Values: file name
Default Value: FFTW_NAMD_version_platform.txt
Description: File where FFTW wisdom is read and saved.
If you only run on one platform this may be useful to reduce startup times for all runs.
The default is likely sufficient, as it is version and platform specific.
The multilevel summation method (MSM) [40]
is an alternative to PME for calculating full electrostatic interactions.
The use of the FFT in PME has two drawbacks:
(1) it generally requires the use of periodic boundary conditions,
in which the simulation describes an infinite three-dimensional lattice,
with each lattice cell containing a copy of the simulated system, and
(2) calculation of the FFT becomes a considerable performance bottleneck
to the parallel scalability of MD simulations, due to the many-to-many
communication pattern employed.
MSM avoids the use of the FFT in its calculation,
instead employing the nested interpolation in real space
of softened pair potentials,
which permits in addition to periodic boundary conditions
the use of
semi-periodic boundaries, in which there is periodicity along
just one or two basis vectors,
or non-periodic boundaries, in which the simulation is
performed in a vacuum.
Also, better parallel scaling has been observed with MSM
when scaling a sufficiently large system to a large number of processors.
See the MSM research web page (http://www.ks.uiuc.edu/Research/msm/)
for more information.
In order to use the MSM,
one need only specify ``MSM on'' in the configuration file.
For production use,
we presently recommend using the default
``MSMQuality 0''
( cubic interpolation with
cubic interpolation with 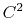 Taylor splitting),
which has been validated to correctly reproduce
the PME results [40].
At this time, we discourage use of the higher order interpolation schemes
(Hermite, quintic, etc.),
as they are still under development.
With cubic interpolation, MSM now gets roughly half the performance of PME.
Comparable performance and better scaling for MSM
have been observed with the optimizations described
in Ref. [40], which will be available shortly.
Taylor splitting),
which has been validated to correctly reproduce
the PME results [40].
At this time, we discourage use of the higher order interpolation schemes
(Hermite, quintic, etc.),
as they are still under development.
With cubic interpolation, MSM now gets roughly half the performance of PME.
Comparable performance and better scaling for MSM
have been observed with the optimizations described
in Ref. [40], which will be available shortly.
For now, NAMD's implementation of the MSM
does not calculate the long-range electrostatic
contribution to the virial, so use with a barostat for
constant pressure simulation is inappropriate.
(Note that the experiments in Ref. [40]
involving constant pressure simulation with MSM
made use of a custom version that is incompatible with
some other NAMD features, so is not yet available.)
The performance of PME is generally still better for smaller systems
with smaller processor counts.
MSM is the only efficient method in NAMD for calculating
full electrostatics for simulations with semi-periodic or
non-periodic boundaries.
The periodicity is defined through setting the cell basis vectors
appropriately, as discussed in Sec. 7.
The cutoff distance, discussed earlier in this section,
also determines the splitting distance between the
MSM short-range part, calculated exactly, and long-range part,
interpolated from the grid hierarchy;
this splitting distance is the primary control for
accuracy for a given interpolation and splitting,
although most simulations will likely want to keep the
cutoff set to the CHARMM-prescribed value of 12 Å.
The configuration options specific to MSM are listed below.
A simulation employing non-periodic boundaries in one or more
dimensions might have atoms that attempt to drift beyond
the predetermined extent of the grid.
In the case that an atom does drift beyond the grid,
the simulation will be halted prematurely with an error message.
Several options listed below deal with defining the extent of the
grid along non-periodic dimensions beyond what can be automatically
determined by the initial coordinates.
It is also recommended for non-periodic simulation to
configure boundary restraints to contain the atoms, for instance,
through Tcl boundary forces in Sec. 8.11.
- MSM
 Use multilevel summation method for electrostatics?
Use multilevel summation method for electrostatics? 
Acceptable Values: yes or no
Default Value: no
Description: Turns on multilevel summation method.
- MSMGridSpacing
 spacing between finest level grid points (Å)
spacing between finest level grid points (Å) 
Acceptable Values: positive real
Default Value: 2.5
Description: The grid spacing determines in part the accuracy and efficiency of MSM.
An error versus cost analysis shows that the best tradeoff is setting
the grid spacing to a value close to the inter-particle spacing.
The default value works well in practice for atomic scale simulation.
This value will be exact along non-periodic dimensions.
For periodic dimensions, the grid spacing must evenly divide the
basis vector length; the actual spacing for a desired grid spacing 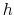 is guaranteed to be within the interval
is guaranteed to be within the interval
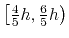 .
.
- MSMQuality
 select the approximation quality
select the approximation quality 
Acceptable Values: 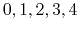
Default Value: 0
Description: This parameter offers a simplified way to select higher order
interpolation and splitting for MSM. The available choices are:
- 0 sets
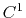 cubic (
cubic (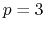 ) interpolation with
) interpolation with 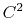 Taylor splitting,
Taylor splitting,
- 1 sets
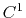 Hermite (
Hermite (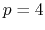 ) interpolation with
) interpolation with 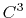 Taylor splitting,
Taylor splitting,
- 2 sets
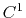 quintic (
quintic (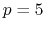 ) interpolation with
) interpolation with 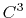 Taylor splitting,
Taylor splitting,
- 3 sets
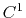 septic (
septic (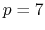 ) interpolation with
) interpolation with 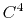 Taylor splitting,
Taylor splitting,
- 4 sets
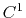 nonic (
nonic (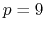 ) interpolation with
) interpolation with 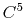 Taylor splitting.
Taylor splitting.
We presently recommend using the default selection,
which has been validated to correctly reproduce
the PME results [40],
and discourage use of the higher order interpolation schemes,
as they are still under development.
With cubic interpolation, MSM now gets roughly half the performance of PME.
Comparable performance and better scaling for MSM
have been observed with the optimizations described
in Ref. [40], which will be available shortly.
There is generally a tradeoff between quality and performance.
Empirical results show that the 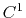 interpolation schemes offer a little
better accuracy than the alternative
interpolation schemes that have greater continuity.
Also, better accuracy has been observed by using
a splitting function with
interpolation schemes offer a little
better accuracy than the alternative
interpolation schemes that have greater continuity.
Also, better accuracy has been observed by using
a splitting function with
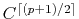 continuity
where
continuity
where 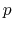 is the order of the interpolant.
is the order of the interpolant.
- MSMApprox
 select the interpolant
select the interpolant 
Acceptable Values:
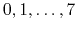
Default Value: 0
Description: Select the interpolation scheme:
- 0 sets
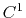 cubic (
cubic (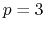 ) interpolation,
) interpolation,
- 1 sets
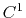 quintic (
quintic (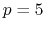 ) interpolation,
) interpolation,
- 2 sets
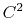 quintic (
quintic (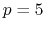 ) interpolation,
) interpolation,
- 3 sets
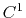 septic (
septic (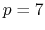 ) interpolation,
) interpolation,
- 4 sets
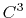 septic (
septic (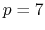 ) interpolation,
) interpolation,
- 5 sets
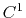 nonic (
nonic (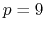 ) interpolation,
) interpolation,
- 6 sets
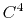 nonic (
nonic (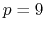 ) interpolation,
) interpolation,
- 7 sets
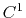 Hermite (
Hermite (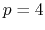 ) interpolation.
) interpolation.
- MSMSplit
 select the splitting
select the splitting 
Acceptable Values:
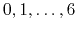
Default Value: 0
Description: Select the splitting function:
- 0 sets
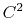 Taylor splitting,
Taylor splitting,
- 1 sets
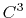 Taylor splitting,
Taylor splitting,
- 2 sets
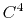 Taylor splitting,
Taylor splitting,
- 3 sets
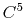 Taylor splitting,
Taylor splitting,
- 4 sets
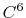 Taylor splitting,
Taylor splitting,
- 5 sets
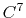 Taylor splitting,
Taylor splitting,
- 6 sets
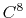 Taylor splitting.
Taylor splitting.
- MSMLevels
 maximum number of levels
maximum number of levels 
Acceptable Values: non-negative integer
Default Value: 0
Description: Set the maximum number of levels to use in the grid hierarchy.
Although setting slightly lower than the default might (or might not)
improve performance and/or accuracy for non-periodic simulation,
it is generally best to leave this at the default value "0" which will
then automatically adjust the levels to the size of the given system.
- MSMPadding
 grid padding (Å)
grid padding (Å) 
Acceptable Values: non-negative real
Default Value: 2.5
Description: The grid padding applies only to non-periodic dimensions, for which
the extent of the grid is automatically determined by the
maximum and minimum of the initial coordinates plus the padding value.
- MSMxmin, MSMymin, MSMzmin
 minimum x-, y-, z-coordinate (Å)
minimum x-, y-, z-coordinate (Å) 
Acceptable Values: real
Description: Set independently the minimum x-, y-, or z-coordinates of
the simulation. This parameter is applicable only to non-periodic dimensions.
It is useful in conjunction with setting a boundary restraining force
with Tcl boundary forces in Sec. 8.11.
- MSMxmax, MSMymax, MSMzmax
 maximum x-, y-, z-coordinate (Å)
maximum x-, y-, z-coordinate (Å) 
Acceptable Values: real
Description: Set independently the maximum x-, y-, or z-coordinates of
the simulation. This parameter is applicable only to non-periodic dimensions.
It is useful in conjunction with setting a boundary restraining force
with Tcl boundary forces in Sec. 8.11.
- MSMBlockSizeX, MSMBlockSizeY, MSMBlockSizeZ
 block size for grid decomposition
block size for grid decomposition 
Acceptable Values: positive integer
Default Value: 8
Description: Tune parallel performance by adjusting the block size used for parallel
domain decomposition of the grid. Recommended to keep the default.
- MSMSerial
 Use serial long-range solver?
Use serial long-range solver? 
Acceptable Values: yes or no
Default Value: no
Description: Enable instead the slow serial long-range solver.
Intended to be used only for testing and diagnostic purposes.
The direct computation of electrostatics
is not intended to be used during
real calculations, but rather as a testing or
comparison measure. Because of the
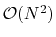 computational complexity for performing
direct calculations, this is much
slower than using PME or MSM to compute full
electrostatics for large systems.
In the case of periodic boundary conditions,
the nearest image convention is used rather than a
full Ewald sum.
computational complexity for performing
direct calculations, this is much
slower than using PME or MSM to compute full
electrostatics for large systems.
In the case of periodic boundary conditions,
the nearest image convention is used rather than a
full Ewald sum.
- FullDirect
 calculate full electrostatics directly?
calculate full electrostatics directly? 
Acceptable Values: yes or no
Default Value: no
Description: Specifies whether or not direct computation of
full electrostatics should be performed.
In order to support coarse grained models and semiconductor force fields,
the tabulated energies feature replaces the normal van der Waals potential
for specified pairs of atom types with one interpolated from user-supplied
energy tables. The electrostatic potential is not altered.
Pairs of atom types to which the modified interactions apply are specified
in a CHARMM parameter file by an NBTABLE section consisting of lines
with two atom types and a corresponding interaction type name.
For example, tabulated interactions for SI-O, O-O, and SI-SI pairs would
be specified in a parameter file as:
NBTABLE
SI O SIO
O O OO
SI SI SISI
Each interaction type must correspond to an entry in the energy table file.
The table file consists of a header formatted as:
# multiple comment lines
<number_of_tables> <table_spacing (A)> <maximum_distance (A)>
followed by number_of_tables energy tables formatted as:
TYPE <interaction type name>
0 <energy (kcal/mol)> <force (kcal/mol/A)>
<table_spacing> <energy (kcal/mol)> <force (kcal/mol/A)>
<2*table_spacing> <energy (kcal/mol)> <force (kcal/mol/A)>
<3*table_spacing> <energy (kcal/mol)> <force (kcal/mol/A)>
...
<maximum_distance - 3*table_spacing> <energy (kcal/mol)> <force (kcal/mol/A)>
<maximum_distance - 2*table_spacing> <energy (kcal/mol)> <force (kcal/mol/A)>
<maximum_distance - table_spacing> <energy (kcal/mol)> <force (kcal/mol/A)>
The table entry at maximum_distance will match the energy of the
previous entry but have a force of zero. The maximum distance must be at
least equal to the nonbonded cutoff distance and entries beyond the cutoff
distance will be ignored. For the above example with a cutoff of 12 Å the table file could look like:
# parameters for silicon dioxide
3 0.01 14.0
TYPE SIO
0 5.092449e+26 3.055469e+31
0.01 5.092449e+14 3.055469e+17
0.02 7.956951e+12 2.387085e+15
0.03 6.985526e+11 1.397105e+14
...
13.98 0.000000e+00 -0.000000e+00
13.99 0.000000e+00 -0.000000e+00
TYPE OO
0 1.832907e+27 1.099744e+32
0.01 1.832907e+15 1.099744e+18
0.02 2.863917e+13 8.591751e+15
0.03 2.514276e+12 5.028551e+14
...
13.98 0.000000e+00 -0.000000e+00
13.99 0.000000e+00 -0.000000e+00
TYPE SISI
0 0.000000e+00 -0.000000e+00
0.01 0.000000e+00 -0.000000e+00
...
13.98 0.000000e+00 -0.000000e+00
13.99 0.000000e+00 -0.000000e+00
The following three parameters are required for tabulated energies.




Next: Water Models
Up: Force Field Parameters
Previous: Potential energy functions
Contents
Index
http://www.ks.uiuc.edu/Research/namd/




![]() cubic interpolation with
cubic interpolation with ![]() Taylor splitting),
which has been validated to correctly reproduce
the PME results [40].
At this time, we discourage use of the higher order interpolation schemes
(Hermite, quintic, etc.),
as they are still under development.
With cubic interpolation, MSM now gets roughly half the performance of PME.
Comparable performance and better scaling for MSM
have been observed with the optimizations described
in Ref. [40], which will be available shortly.
Taylor splitting),
which has been validated to correctly reproduce
the PME results [40].
At this time, we discourage use of the higher order interpolation schemes
(Hermite, quintic, etc.),
as they are still under development.
With cubic interpolation, MSM now gets roughly half the performance of PME.
Comparable performance and better scaling for MSM
have been observed with the optimizations described
in Ref. [40], which will be available shortly.
![]() interpolation schemes offer a little
better accuracy than the alternative
interpolation schemes that have greater continuity.
Also, better accuracy has been observed by using
a splitting function with
interpolation schemes offer a little
better accuracy than the alternative
interpolation schemes that have greater continuity.
Also, better accuracy has been observed by using
a splitting function with
![]() continuity
where
continuity
where ![]() is the order of the interpolant.
is the order of the interpolant.
![]() computational complexity for performing
direct calculations, this is much
slower than using PME or MSM to compute full
electrostatics for large systems.
In the case of periodic boundary conditions,
the nearest image convention is used rather than a
full Ewald sum.
computational complexity for performing
direct calculations, this is much
slower than using PME or MSM to compute full
electrostatics for large systems.
In the case of periodic boundary conditions,
the nearest image convention is used rather than a
full Ewald sum.