



Next: Linear restraints
Up: Biasing and analysis methods
Previous: Computing the work of
Contents
Index
The harmonicWalls {...} bias is closely related to the harmonic bias (see ![[*]](crossref.png) ), with the following two differences: (i) instead of a center a lower wall and/or an upper wall are defined, outside of which the bias implements a half-harmonic potential;
), with the following two differences: (i) instead of a center a lower wall and/or an upper wall are defined, outside of which the bias implements a half-harmonic potential;
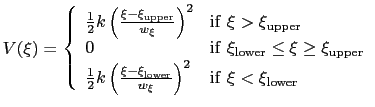 |
(13.36) |
where
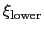 and
and
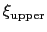 are the lower and upper wall thresholds, respectively; (ii) because an interval between two walls is defined, only scalar variables can be used (but any number of variables can be defined, and the wall bias is intrinsically multi-dimensional).
are the lower and upper wall thresholds, respectively; (ii) because an interval between two walls is defined, only scalar variables can be used (but any number of variables can be defined, and the wall bias is intrinsically multi-dimensional).
Note: this bias replaces the keywords lowerWall, lowerWallConstant, upperWall and upperWallConstant defined in the colvar context.
Those keywords are deprecated.
The harmonicWalls bias implements the following options:
-
name: see definition of name (biasing and analysis methods)
-
colvars: see definition of colvars (biasing and analysis methods)
-
outputEnergy: see definition of outputEnergy (biasing and analysis methods)
-
writeTIPMF: see definition of writeTIPMF (biasing and analysis methods)
-
writeTISamples: see definition of writeTISamples (biasing and analysis methods)
-
stepZeroData: see definition of stepZeroData (biasing and analysis methods)
-
lowerWalls
 Position of the lower wall
Position of the lower wall
Context: colvar
Acceptable values: Space-separated list of decimals
Description: Defines the values
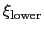 below which a confining restraint on the colvar is applied to each colvar
below which a confining restraint on the colvar is applied to each colvar 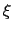 .
.
-
upperWalls
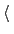 Position of the lower wall
Position of the lower wall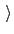
Context: colvar
Acceptable values: Space-separated list of decimals
Description: Defines the values
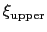 above which a confining restraint on the colvar is applied to each colvar
above which a confining restraint on the colvar is applied to each colvar 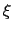 .
.
-
forceConstant: see definition of forceConstant (Harmonic restraints)
-
lowerWallConstant
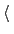 Force constant for the lower wall
Force constant for the lower wall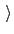
Context: harmonicWalls
Acceptable values: positive decimal
Default value: forceConstant
Description: When both sets of walls are defined (lower and upper), this keyword allows setting different force constants for them.
As with forceConstant, the specified constant is divided internally by the square of the specific width of each variable (see also the equivalent keyword for the harmonic restraint, forceConstant).
The force constant reported in the output as ``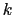 '', and used in the change of force constant scheme, is the geometric mean of upperWallConstant and upperWallConstant.
'', and used in the change of force constant scheme, is the geometric mean of upperWallConstant and upperWallConstant.
-
upperWallConstant: analogous to lowerWallConstant
-
targetForceConstant: see definition of targetForceConstant (harmonic restraints)
-
targetForceConstant
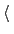 Change the force constant(s) towards this value
Change the force constant(s) towards this value
Context: harmonicWalls
Acceptable values: positive decimal
Description: This keyword allows changing either one or both of the wall force constants over time.
In the case that lowerWallConstant and upperWallConstant have the same value, the behavior of this keyword is identical to the corresponding keyword in the harmonic restraint; otherwise, the change schedule is applied to the geometric mean of the two constant.
When only one set of walls is defined (lowerWall or upperWalls), only the respective force constant is changed.
Note: if only one of the two force constants is meant to change over time, it is possible to use two instances of harmonicWalls, and apply the changing schedule only to one of them.
-
targetNumSteps: see definition of targetNumSteps (harmonic restraints)
-
targetForceExponent: see definition of targetForceExponent (harmonic restraints)
-
targetEquilSteps: see definition of targetEquilSteps (harmonic restraints)
-
targetNumStages: see definition of targetNumStages (harmonic restraints)
-
lambdaSchedule: see definition of lambdaSchedule (harmonic restraints)
-
outputAccumulatedWork: see definition of outputAccumulatedWork (harmonic restraints)
-
bypassExtendedLagrangian
 Apply bias to actual colvars, bypassing extended coordinates
Apply bias to actual colvars, bypassing extended coordinates
Context: harmonicWalls
Acceptable values: boolean
Default value: on
Description: This option behaves as bypassExtendedLagrangian for other biases,
but it defaults to on, unlike in the general case.
Thus, by default, the harmonicWalls bias applies to the actual colvars, so that the distribution of the colvar between the walls is unaffected by the bias, which then applies a flat-bottom potential as a function of the colvar value. This bias will affect the extended coordinate distribution near the walls.
If bypassExtendedLagrangian is disabled, harmonicWalls applies a flat-bottom potential as a function of the extended coordinate. Conversely, this bias will then modify the distribution of the actual colvar value near the walls.
Example 1: harmonic walls for one variable with two different force constants.
harmonicWalls {
name mywalls
colvars dist
lowerWalls 22.0
upperWalls 38.0
lowerWallConstant 2.0
upperWallConstant 10.0
}
Example 2: harmonic walls for two variables with a single force constant.
harmonicWalls {
name mywalls
colvars phi psi
lowerWalls -180.0 0.0
upperWalls 0.0 180.0
forceConstant 5.0
}




Next: Linear restraints
Up: Biasing and analysis methods
Previous: Computing the work of
Contents
Index
vmd@ks.uiuc.edu
![[*]](crossref.png) ), with the following two differences: (i) instead of a center a lower wall and/or an upper wall are defined, outside of which the bias implements a half-harmonic potential;
), with the following two differences: (i) instead of a center a lower wall and/or an upper wall are defined, outside of which the bias implements a half-harmonic potential;
![[*]](crossref.png) ), with the following two differences: (i) instead of a center a lower wall and/or an upper wall are defined, outside of which the bias implements a half-harmonic potential;
), with the following two differences: (i) instead of a center a lower wall and/or an upper wall are defined, outside of which the bias implements a half-harmonic potential;