|
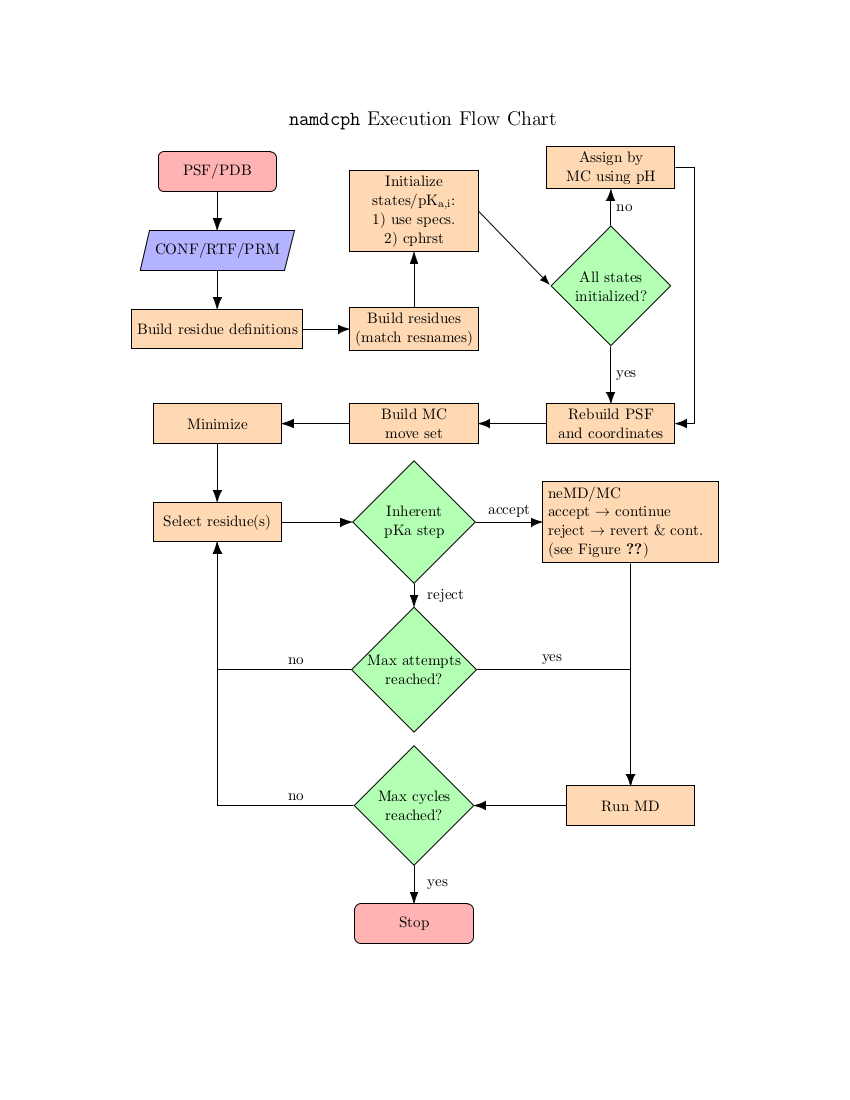
In NAMD, each canonical partition function is represented by a specific force field description embodied in a PSF - in order to change the protonation state the underlying PSF must also be modified. This is accomplished by a close coupling to psfgen. The models that can be used with constant-pH MD are thus limited to only those which can be completely implemented within psfgen. This also means that NAMD requires access to residue topology files (RTFs) during the course of a simulation. These must be specified with the psfgen topology command.
For consistency between topological descriptions, NAMD uses ``dummy'' atoms to represent non-interacting protons. These atoms have the same mass as protons but only interact with the system via a minimal number of force field bonded terms. This formalism guarantees that: 1) the number of atoms/coordinates during the simulation remains fixed and 2) the thermodynamics of the model is unchanged. The latter point is subtle and warrants comment. As implemented in NAMD, constant-pH MD only captures the thermodynamics of the semi-grand canonical ensemble. There is no active description of proton dissociation events. However, this is more of a limitation of classical MD than a particular shortcoming of NAMD. A useful analogy may be the use of Langevin dynamics as a thermostat as opposed to a phenomonological model for Brownian motion.

|
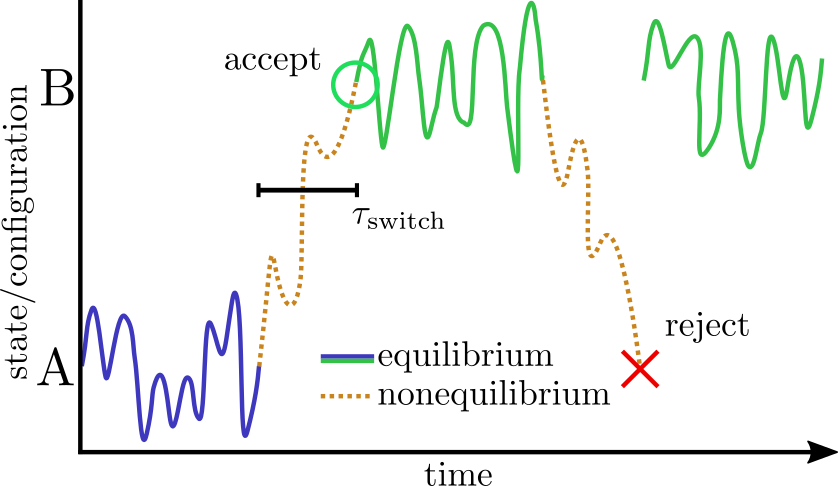
The basic scheme in NAMD is to alternately sample the protonation state and then the configuration space within that state. Protonation state sampling is accomplished by an alchemical coupling scheme that forcibly turns off interactions with the current protonation state and turns on interactions with a candidate protonation state. This nonequilibrium ``switching'' is accomplished with the alchemy code (specifically the thermodynamic integration code branch) and necessarily has lower performance (by about 30%) than regular MD due to the added electrostatic calculations in the reciprocal space (i.e., when using PME). However, the configuration space sampling should still have normal performance. The switching process exerts work on the system and thus drives the system out of equilibrium. However, an appropriately designed Monte Carlo (MC) move using an accept/reject criterion can recover the correct semi-grand canonical equilibrium distribution in both the state and configuration spaces [81,20]. The resulting scheme is a hybrid nonequilibrium MD/MC (neMD/MC) algorithm. The most important conceptual change from conventional MD is that, rather than being a continuous trajectory, the simulation now becomes a series of cycles composed of an MD and neMD/MC step. This means that the length of the simulation is no longer simply determined by the number of steps (numsteps) but rather the number of cycles. The length of a cycle is also determined by two parts - the amount of time on equilibrium sampling and the amount of time executing the switch.
It may be profitable/necessary to vary the switch time depending on the type of
protonation change that is being effected.
Indeed, this is a critical factor in the efficiency of the method.
That is, if the switch is too short, then moves are unlikely to be accepted and
effort will be wasted when the move is rejected.
However, if the switch is too long, then an inordinate amount of effort will be
spent sampling the state space and there will be fewer resources left for
exploring the configuration space.
Some basic qualities of the system that affect sampling have been determined
using nonequilibrium linear response
theory [89].
In short, there are intrinsic limits based on:
1) the extent that differing interactions between each state fluctuate
(according to some variance,
![]() )
and
2) the ``molecular'' time scale,
)
and
2) the ``molecular'' time scale,
![]() , on which these
fluctuations change.
These effects are roughly captured by the
expression [89,88]:
, on which these
fluctuations change.
These effects are roughly captured by the
expression [89,88]:
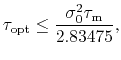 |
![\fbox{
\begin{minipage}[ht!]{15.3cm}
\addtolength{\baselineskip}{0.225\baselin...
...y modest additional
developments. %(see Notes for Developers).
\end{minipage}}](img697.png)