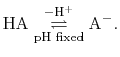



Next: Implementation Details
Up: Constant-pH Simulations 1
Previous: Constant-pH Simulations 1
Contents
Index
Constant-pH MD is a simulation methodology specially formulated for the
treatment of variable protonation states.
This is to be contrasted with conventional force-field based MD simulations,
which generally treat protonation states by assuming they are fixed.
Consider, for example, a protein with two titratable residues which may both be
either protonated or deprotonated (Figure 13);
the system has four possible protonation states.
In the conventional route, the user must enumerate these possibilities,
construct distinct topologies, and then simulate the cases individually.
The simulations for each state must then be connected by either asserting
knowledge about the system (e.g., by assuming that only certain
states are of biological importance) or by performing additional simulations
to probe transitions between states directly (e.g., by performing
free energy calculations).
In a constant-pH MD simulation, knowledge of the transformations is not
assumed and is instead actively explored by interconverting between the
various protonation states.
This is especially useful when the number of protonation states is extremely
large and/or prior information on the importance of particular states is
not available.
Figure:
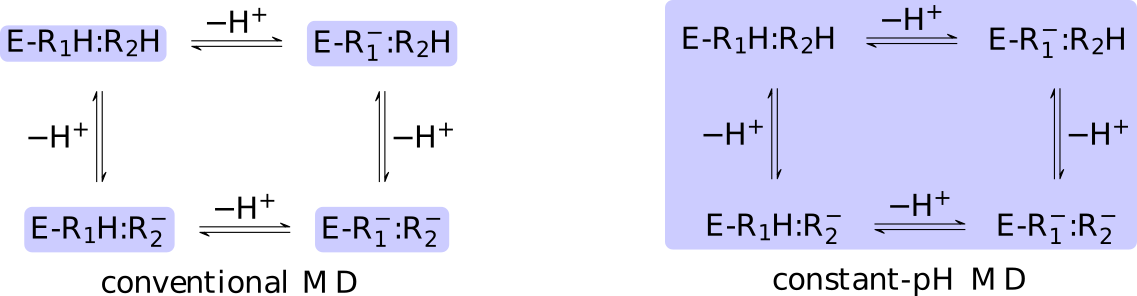
The core difference between conventional and constant-pH MD can be
illustrated by a simple enzyme  with four protonation states
describing the occupancy of two titratable residues,
with four protonation states
describing the occupancy of two titratable residues,  and
and  .
A conventional MD simulation handles the states separately (left
panel).
The relative importance of the states must be known beforehand or computed
by other means.
Conversely, a constant-pH MD simulation handles the states
collectively and actively simulates interconversion (right panel).
Determining the relative importance of the states is a direct result of the
simulation.
.
A conventional MD simulation handles the states separately (left
panel).
The relative importance of the states must be known beforehand or computed
by other means.
Conversely, a constant-pH MD simulation handles the states
collectively and actively simulates interconversion (right panel).
Determining the relative importance of the states is a direct result of the
simulation.
|
In formal terms, conventional MD samples from a canonical ensemble, whereas
constant-pH MD samples from a semi-grand canonical ensemble.
The new partition function,
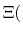 pH pH |
(79) |
is essentially a weighted summation of canonical partition functions,
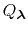 , each of which are defined by an occupancy vector,
, each of which are defined by an occupancy vector,
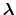 .
The elements of
.
The elements of
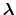 are either one or zero depending on whether a
given protonation site is or is not occupied, respectively.
For a vector of length
are either one or zero depending on whether a
given protonation site is or is not occupied, respectively.
For a vector of length 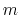 , the set of all protonation states,
, the set of all protonation states,
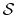 ,
has at most
,
has at most 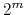 members.
In order to sample from the corresponding semi-grand canonical distribution
function, a simulation must explore both the phase space defined by
the canonical paritition functions and the state space defined by the
different occupancy vectors.
The fraction of simulation time spent in each state is dictated by the weights
in the summation and these depend on the pH and the number of protons,
members.
In order to sample from the corresponding semi-grand canonical distribution
function, a simulation must explore both the phase space defined by
the canonical paritition functions and the state space defined by the
different occupancy vectors.
The fraction of simulation time spent in each state is dictated by the weights
in the summation and these depend on the pH and the number of protons,
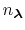 , in the system (i.e., the sum of the
elements in
, in the system (i.e., the sum of the
elements in
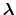 ).
).
Although a constant-pH MD system may contain any number of titratable protons,
the base transformation is always the movement of one proton from a
molecule into a bath of non-interacting protons ``in solution.''
For a generic chemical species A, this corresponds to the usual deprotonation
reaction definition, except with fixed pH:
In the language of statistical mechanics the species HA and A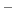 refer to
all terms in Eq. (80) which do and do not, respectively,
contain the specific proton in question (i.e., the particular
element of
refer to
all terms in Eq. (80) which do and do not, respectively,
contain the specific proton in question (i.e., the particular
element of
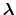 is one or zero).
By taking out a factor of
is one or zero).
By taking out a factor of
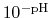 , this can be re-written as
, this can be re-written as
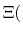 pH pH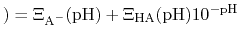 |
|
and then recast as a statistical mechanical analog of the
Henderson-Hasselbalch equation by recognizing that
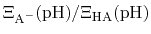 is just the
ratio of deprotonated / protonated fractions of species A.
The protonated fraction is then
is just the
ratio of deprotonated / protonated fractions of species A.
The protonated fraction is then
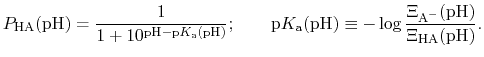 |
(80) |
In practice,
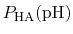 can be calculated from a simulation by
simply counting the fraction of time spent in state HA (e.g., the
fraction of time a specific element of
can be calculated from a simulation by
simply counting the fraction of time spent in state HA (e.g., the
fraction of time a specific element of
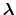 is one).
Note also that
p
is one).
Note also that
p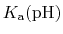 is formally a pH dependent function
unless the system only contains one proton (or type of proton).
is formally a pH dependent function
unless the system only contains one proton (or type of proton).
In most experimental contexts, a different form of Eq. (81) is used
which is often referred to as a ``generalized'' Hill equation.
This corresponds to a specific choice of pH dependence such that
p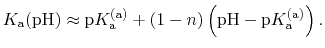 |
|
The constant 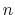 is then known as the Hill coefficient and the so-called
apparent
p
is then known as the Hill coefficient and the so-called
apparent
p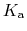 ,
p
,
p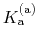 , generally corresponds to the inflection point
of a plot of
, generally corresponds to the inflection point
of a plot of
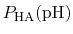 .
Both quantities are usually determined by non-linear regression after
.
Both quantities are usually determined by non-linear regression after
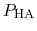 has been determined at different pH values.
has been determined at different pH values.




Next: Implementation Details
Up: Constant-pH Simulations 1
Previous: Constant-pH Simulations 1
Contents
Index
http://www.ks.uiuc.edu/Research/namd/