

Next: About this document ...
Numerical Laboratory
David Hardy, Robert Engle, John Marriott, Wei Wang, Robert Skeel
We are using Mathematica notebooks as a front end.
Before beginning, make sure that you do not
already have Mathematica running.
(Quit out of it if you do.)
To get started,
from the command prompt in your home directory perform
the following commands:
$ mkdir -p tbss.work/numlab create a directory for the notebooks
$ cd tbss.work/numlab make it your current working directory
$ numlab copy over the notebooks and then open the first one
(Note that ``numlab'' is really a symbolic link to the
``tutorials/09-numerical-algorithms/run'' script. If this
symbolic link does not exist in your path, then you can create it
locally by performing
$ link -s /PATH/TO/tutorials/09-numerical-algorithms/run .
and then running the script as ``./numlab''.)
Please be aware that you must always use this script to start the
tutorial in order to configure environmental variables correctly
(otherwise the lab exercises will not work as expected).
Once you begin the tutorial on the first notebook (1.nb),
you later can open others by choosing ``Open'' from the ``File'' menu,
or you can run ``numlab 2.nb'' to explicitly open the
second notebook, etc.
To evaluate a bracketed input ``cell,'' click on it to highlight it
(or click within it to place the cursor inside)
and then press ``shift-enter.'' Some input expressions merely define
functions or variables. Others compute or plot a result.
(There might be some delay while results are computed.)
Generally, you should evaluate the input expressions sequentially.
You may edit input in the usual way and reevaluate by again pressing
``shift-enter.'' You may also cut and paste an expression into a new
cell at the end of the notebook or in between two cells.
You may save your work back to the local notebook copies.
To restore the original notebooks, perform:
$ rm [1-6].nb remove all of the notebooks
$ numlab restore the original notebooks and then open the first one
If there are any problems with Mathematica
behaving unexpectedly on the notebooks,
try quitting out of Mathematica
and then restart with the ``numlab'' command.
Exercises 1, 4, and 5 use NAMD, and exercise 6 uses an experimental
program MDX.
- Chaotic nature of MD trajectories.
- System. Choice of waters or decalanine in vacuum.
- Input. Size of perturbation in initial positions of atoms.
- Output. Printing of time in fs and amplification factor for
RMSD (root mean squared distance) between trajectories.
- Questions. For each system, what is the doubling time for the size
of a perturbation?
- water
- decalanine
- Remark. Your answers will be much smaller than those obtained
from the figures on page 398 of Schlick or page 77 of Allen & Tildesley
because of the presence of unconstrained hydrogen atoms.
- Non-symplectic integration. Standard Verlet is compared to the use of Verlet with velocity rescaling (non-symplectic), where at the end of each step the velocities are rescaled to conserve energy.
If the potential energy exceeds the initial energy,
the velocities are set to zero, and this attempt is counted
as a failure. Rescaling will succeed in a future step.
- System. Henon-Heiles Hamiltonian:
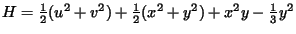 .
Space variables
.
Space variables 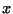 ,
, 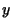 and velocity variables
and velocity variables 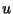 ,
, 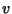 .
.
- Input. Energy, step size, scaling off or on
(an energy
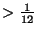 gives a chaotic trajectory,
an energy
gives a chaotic trajectory,
an energy 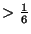 gives a trajectory that goes to the abyss).
gives a trajectory that goes to the abyss).
- Output. Intersection of the energy surface with
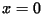 projected onto the y-v plane (Poincaré section).
If the original surface defined by the tail end of
an (infinitely long) trajectory is
projected onto the y-v plane (Poincaré section).
If the original surface defined by the tail end of
an (infinitely long) trajectory is 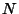 -dimensional, its intersection and
projection will be of dimension
-dimensional, its intersection and
projection will be of dimension 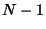 .
The points from the last half of the trajectory are shown
in red color.
.
The points from the last half of the trajectory are shown
in red color.
- Questions. Is the ``hypersurface'' of constant
energy of dimension 3, 2, 1, or 0?
- energy
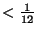 without rescaling
without rescaling
- energy
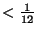 with rescaling
with rescaling
- energy
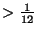 without rescaling
without rescaling
- energy
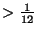 with rescaling
with rescaling
- Remark. There seems to be no clear conclusion in the
case of velocity rescaling.
- Smoothness of potential.
- System. 2 argon atoms with periodic BCs in 2D.
Potential is multiplied by a switching function with continuity
DC, C0, C1, or C2.
- Input. Choice of switching function (DC=0, C0=1,
C1=2 and C2=3),
switching distance (default=6), cutoff (default=8), step size (default=2).
- Output. Energy plot for 200,000 steps.
- Questions. For which switching functions do we get
energy drift?
For which switching functions do we get just fluctuations?
- Resonance. If the step size is close to a simple fraction
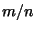 of the numerically
perturbed period of a significant high frequency normal mode, then this is
manifested in the trajectory and energy. In particular, the total energy
will seem to cycle through
of the numerically
perturbed period of a significant high frequency normal mode, then this is
manifested in the trajectory and energy. In particular, the total energy
will seem to cycle through 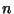 different values.
different values.
- System. Flexible water.
- Input.
Step size (start with the ones we provide).
In a separate cell, guess the
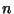 in the resonance order
in the resonance order 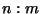 .
.
- Output. Energy for 250 steps.
The guess for
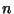 joins every
joins every 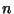 th point, each set with a different color.
th point, each set with a different color.
- Questions. For each step size below,
what order of resonance
(9:4, 7:3, 5:2, 8:3, 3:1, 10:3, 7:2, 4:1, 9:2, 5:1, 6:1, 7:1, 8:1, 9:1, 10:1)
do you observe?
- 2.78452
- 2.51381
- 1.8899
- 1.23044
- 0.993579
- Order of accuracy. I. The order of accuracy is
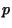 if the error
if the error
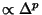 as
as
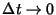 .
.
- System. Badly equilibrated alanine dipeptide.
- Input. Largest of 3 step sizes.
- Output. The end to end distance
between two oxygens for 250 steps for a given step size,
half of that step size, and a quarter of that step size --
as a function of time.
- Questions. By what factor does error decrease if step size
is halved?
- Order of accuracy. II.
- System. Badly equilibrated decalanine and water.
- Input. The larger of 2 step sizes.
- Output. Error in energy and error in shadow energy
for 250 steps for the given step size and
half of that step size -- as a function of time.
- Questions. By what factor does error decrease if step size
is halved?


Next: About this document ...
David Hardy
2003-06-30
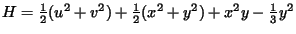 .
Space variables
.
Space variables 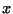 ,
, 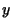 and velocity variables
and velocity variables 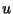 ,
, 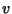 .
.
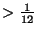 gives a chaotic trajectory,
an energy
gives a chaotic trajectory,
an energy 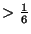 gives a trajectory that goes to the abyss).
gives a trajectory that goes to the abyss).
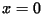 projected onto the y-v plane (Poincaré section).
If the original surface defined by the tail end of
an (infinitely long) trajectory is
projected onto the y-v plane (Poincaré section).
If the original surface defined by the tail end of
an (infinitely long) trajectory is 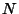 -dimensional, its intersection and
projection will be of dimension
-dimensional, its intersection and
projection will be of dimension 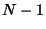 .
The points from the last half of the trajectory are shown
in red color.
.
The points from the last half of the trajectory are shown
in red color.
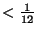 without rescaling
without rescaling
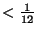 with rescaling
with rescaling
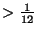 without rescaling
without rescaling
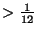 with rescaling
with rescaling
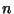 in the resonance order
in the resonance order 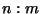 .
.
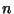 joins every
joins every 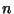 th point, each set with a different color.
th point, each set with a different color.